Enhancing Query Optimization in Production: A Microsoft Journey
Explore Microsoft's innovative approach to query optimization in production environments, addressing challenges with general-purpose optimization and introducing specialized cloud-based optimizers. Learn about the implementation details, experiments conducted, and the solution proposed. Discover how
2 views • 27 slides
Stochastic Storm Transposition in HEC-HMS: Modern Techniques and Applications
Explore the innovative methods and practical applications of Stochastic Storm Transposition (SST) in the context of HEC-HMS. Delve into the history, fundamentals, simulation procedures, and benefits of using SST for watershed-averaged precipitation frequency analysis. Learn about the non-parametric
3 views • 41 slides
Understanding Swarm Intelligence: Concepts and Applications
Swarm Intelligence (SI) is an artificial intelligence technique inspired by collective behavior in nature, where decentralized agents interact to achieve goals. Swarms are loosely structured groups of interacting agents that exhibit collective behavior. Examples include ant colonies, flocking birds,
2 views • 88 slides
Understanding Spherical Mirrors: Concave and Convex Types, Image Formation, and Practical Uses
Spherical mirrors, including concave and convex types, play a crucial role in reflecting light. By exploring the properties of concave and convex mirrors, understanding image formation, and discovering their diverse applications in daily life, we can grasp the significance of these mirrors in scienc
0 views • 9 slides
DNN Inference Optimization Challenge Overview
The DNN Inference Optimization Challenge, organized by Liya Yuan from ZTE, focuses on optimizing deep neural network (DNN) models for efficient inference on-device, at the edge, and in the cloud. The challenge addresses the need for high accuracy while minimizing data center consumption and inferenc
0 views • 13 slides
Panel Stochastic Frontier Models with Endogeneity in Stata
Introducing xtsfkk, a new Stata command for fitting panel stochastic frontier models with endogeneity, offering better control for endogenous variables in the frontier and/or the inefficiency term in longitudinal settings compared to standard estimators. Learn about the significance of stochastic fr
0 views • 13 slides
Understand Convex and Concave Functions in Mathematics
Learn about convex and concave functions in mathematics, including how to differentiate between them, identify their characteristics, and analyze gradients. Explore the concepts with practical examples and visual aids. Enhance your proficiency in answering questions related to convex and concave fun
0 views • 15 slides
Understanding Discrete Optimization in Mathematical Modeling
Discrete Optimization is a field of applied mathematics that uses techniques from combinatorics, graph theory, linear programming, and algorithms to solve optimization problems over discrete structures. This involves creating mathematical models, defining objective functions, decision variables, and
0 views • 12 slides
Generalization of Empirical Risk Minimization in Stochastic Convex Optimization by Vitaly Feldman
This study delves into the generalization of Empirical Risk Minimization (ERM) in stochastic convex optimization, focusing on minimizing true objective functions while considering generalization errors. It explores the application of ERM in machine learning and statistics, particularly in supervised
0 views • 11 slides
Understanding Stability and Generalization in Machine Learning
Exploring high probability generalization bounds for uniformly stable algorithms, the relationship between dataset, loss function, and estimation error, and the implications of low sensitivity on generalization. Known bounds and new theoretical perspectives are discussed, along with approaches like
0 views • 8 slides
Generalization Bounds and Algorithms in Machine Learning
Generalization bounds play a crucial role in assessing the performance of machine learning algorithms. Uniform stability, convex optimization, and error analysis are key concepts in understanding the generalization capabilities of algorithms. Stability in optimization, gradient descent techniques, a
0 views • 16 slides
Understanding Optimization Techniques in Neural Networks
Optimization is essential in neural networks to find the minimum value of a function. Techniques like local search, gradient descent, and stochastic gradient descent are used to minimize non-linear objectives with multiple local minima. Challenges such as overfitting and getting stuck in local minim
0 views • 9 slides
Optimization Techniques in Convex and General Problems
Explore the world of optimization through convex and general problems, understanding the concepts, constraints, and the difference between convex and non-convex optimization. Discover the significance of local and global optima in solving complex optimization challenges.
0 views • 24 slides
Closest Pair and Convex Hull: Brute Force Approach
Closest Pair Problem in 2D involves finding the two closest points in a set by computing the distance between every pair of distinct points. The Convex Hull Problem determines the smallest convex polygon covering a set of points. Dr. Sasmita Kumari Nayak explains these concepts using a brute-force a
0 views • 15 slides
Understanding Convex Hulls in Computational Geometry
Convex hulls are a fundamental concept in computational geometry, representing the smallest convex shape that contains a set of points. The process involves defining the convexity of a set, determining the unique convex polygon, and computing the convex hull efficiently using algorithms. This conten
0 views • 9 slides
Algorithms: Convex Hull, Strassen's Matrix Multiplication, and More
Explore various divide-and-conquer algorithms including Convex Hull, Strassen's Matrix Multiplication, and Quickhull. Understand the concepts of Sorting, Closest Pairs, and Efficiency in algorithm design. Discover efficient techniques such as recursive calculations and simplifications to enhance alg
1 views • 20 slides
Stochastic Coastal Regional Uncertainty Modelling II (SCRUM2) Overview
SCRUM2 project aims to enhance CMEMS through regional/coastal ocean-biogeochemical uncertainty modelling, ensemble consistency verification, probabilistic forecasting, and data assimilation. The research team plans to contribute significant advancements in ensemble techniques and reliability assessm
0 views • 28 slides
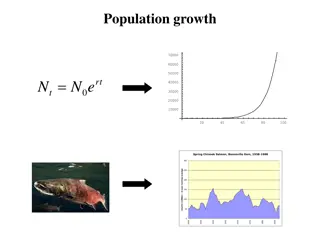
Understanding Population Growth Models and Stochastic Effects
Explore the simplest model of population growth and the assumptions it relies on. Delve into the challenges of real-world scenarios, such as stochastic effects caused by demographic and environmental variations in birth and death rates. Learn how these factors impact predictions and models.
0 views • 35 slides
Insights into Recent Progress on Sampling Problems in Convex Optimization
Recent research highlights advancements in solving sampling problems in convex optimization, exemplified by works by Yin Tat Lee and Santosh Vempala. The complexity of convex problems, such as the Minimum Cost Flow Problem and Submodular Minimization, are being unraveled through innovative formulas
1 views • 47 slides
Convex Optimization: Interior Point Methods Formulation
This chapter on interior point methods in convex optimization explores the formulation of inequality-constrained optimization problems using barrier methods and generalized inequalities. It covers primal-dual interior point methods and discusses issues such as exponential complexity and determining
0 views • 24 slides
Exploring Links Between Convex Geometry and Query Processing
Delve into the intersection of convex geometry and query processing at Stanford University, where theoretical discussions are being applied to real-world database engine development. Learn about the optimization of database joins, the historical evolution of database engines, and the challenges face
0 views • 54 slides
Optics Solved Problems: How to Solve for Focal Lengths
This content provides solutions to various optics problems involving thick lenses, double convex lenses, bi-convex lenses, compound lenses, and more. It covers topics such as identifying principal and focal points, calculating image distances, determining the effective focal length of lens systems,
1 views • 12 slides
Multiserver Stochastic Scheduling Analysis
This presentation delves into the analysis and optimality of multiserver stochastic scheduling, focusing on the theory of large-scale computing systems, queueing theory, and prior work on single-server and multiserver scheduling. It explores optimizing response time and resource efficiency in modern
0 views • 38 slides
Approximation Algorithms for Stochastic Optimization: An Overview
This piece discusses approximation algorithms for stochastic optimization problems, focusing on modeling uncertainty in inputs, adapting to stochastic predictions, and exploring different optimization themes. It covers topics such as weakening the adversary in online stochastic optimization, two-sta
0 views • 33 slides
Advanced Subpath Algorithms for Convex Hull Queries
This study presents innovative algorithms for subpath convex hull queries, focusing on efficient computation of convex hulls for subpaths between two vertices on a simple path in the plane. The work includes a comparison with previous methods, showcasing improvements in space complexity and query pr
0 views • 19 slides
Understanding Convex Hulls in Computational Geometry
Convex hulls play a vital role in computational geometry, enabling shape approximation, collision avoidance in robotics, and finding smallest enclosing boxes for point sets. The convex hull problem involves computing the smallest convex polygon containing a set of points, with extreme points determi
0 views • 119 slides
Optimal Sustainable Control of Forest Sector with Stochastic Dynamic Programming and Markov Chains
Stochastic dynamic programming with Markov chains is used for optimal control of the forest sector, focusing on continuous cover forestry. This approach optimizes forest industry production, harvest levels, and logistic solutions based on market conditions. The method involves solving quadratic prog
0 views • 27 slides
Integrating Stochastic Weather Generator with Climate Change Projections for Water Resource Analysis
Exploring the use of a stochastic weather generator combined with downscaled General Circulation Models for climate change analysis in the California Department of Water Resources. The presentation outlines the motivation, weather-regime based generator description, scenario generation, and a case s
0 views • 20 slides
Optimizing Multi-Party Video Conferencing through Server Selection and Topology Control
This paper proposes innovative methods for multi-server placement and topology control in multi-party video conferences. It introduces a three-step procedure to minimize end-to-end delays between client pairs using D-Grouping and convex optimization. The study demonstrates how combining D-Grouping,
0 views • 13 slides
Understanding Stochastic Differential Equations and Numerical Integration
Explore the concepts of Brownian motion, integration of stochastic differential equations, and derivations by Einstein and Langevin. Learn about the assumptions, forces, and numerical integration methods in the context of stochastic processes. Discover the key results and equations that characterize
0 views • 6 slides
Flower Pollination Algorithm: Nature-Inspired Optimization
Real-world design problems often require multi-objective optimization, and the Flower Pollination Algorithm (FPA) developed by Xin-She Yang in 2012 mimics the pollination process of flowering plants to efficiently solve such optimization tasks. FPA has shown promising results in extending to multi-o
0 views • 15 slides
Introduction to Generalized Stochastic Petri Nets (GSPN) in Manufacturing Systems
Explore Generalized Stochastic Petri Nets (GSPN) to model manufacturing systems and evaluate steady-state performances. Learn about stochastic Petri nets, inhibitors, priorities, and their applications through examples. Delve into models of unreliable machines, productions systems with priorities, a
0 views • 44 slides
Exploring Stochastic Algorithms: Monte Carlo and Las Vegas Variations
Stochastic algorithms, including Monte Carlo and Las Vegas variations, leverage randomness to tackle complex tasks efficiently. While Monte Carlo algorithms prioritize speed with some margin of error, Las Vegas algorithms guarantee accuracy but with variable runtime. They play a vital role in primal
0 views • 13 slides
Optimal Early Drought Detection Using Stochastic Process
Explore an optimal stopping approach for early drought detection, focusing on setting trigger levels based on precipitation measures. The goal is to determine the best time to send humanitarian aid by maximizing expected rewards and minimizing expected costs through suitable gain/risk functions. Tas
0 views • 4 slides
Optimizing User Behavior in Viral Marketing Using Stochastic Control
Explore the world of viral marketing and user behavior optimization through stochastic optimal control in the realm of human-centered machine learning. Discover strategies to maximize user activity in social networks by steering behaviors and understanding endogenous and exogenous events. Dive into
0 views • 15 slides
Machine Learning Applications for EBIS Beam Intensity and RHIC Luminosity Maximization
This presentation discusses the application of machine learning for optimizing EBIS beam intensity and RHIC luminosity. It covers topics such as motivation, EBIS beam intensity optimization, luminosity optimization, and outlines the plan and summary of the project. Collaborators from MSU, LBNL, and
0 views • 23 slides
Understanding Tradeoff between Sample and Space Complexity in Stochastic Streams
Explore the relationship between sample and space complexity in stochastic streams to estimate distribution properties and solve various problems. The research delves into the tradeoff between the number of samples required to solve a problem and the space needed for the algorithm, covering topics s
0 views • 23 slides
Efficient Training of Dense Linear Models on FPGA with Low-Precision Data
Training dense linear models on FPGA with low-precision data offers increased hardware efficiency while maintaining statistical efficiency. This approach leverages stochastic rounding and multivariate trade-offs to optimize performance in machine learning tasks, particularly using Stochastic Gradien
0 views • 26 slides
Fast Bayesian Optimization for Machine Learning Hyperparameters on Large Datasets
Fast Bayesian Optimization optimizes hyperparameters for machine learning on large datasets efficiently. It involves black-box optimization using Gaussian Processes and acquisition functions. Regular Bayesian Optimization faces challenges with large datasets, but FABOLAS introduces an innovative app
0 views • 12 slides
Distributed Optimization and Games (DOG) by Giovanni Neglia
Understand existing distributed algorithms in communication networks, engineer new distributed protocols, and learn how local interactions among agents in a network have global effects. The course offers short tests, examples, case studies, and take-home lessons, focusing on techniques and concepts
0 views • 7 slides