Exploring Complexity and Complicatedness in Travel Demand Modeling Systems
Delve into the intricate world of travel demand modeling systems, where complexity arises from dynamic feedback, stochastic effects, uncertainty, and system structure. Discover the balance needed to minimize complicatedness while maximizing behavioral complexity in regional travel modeling. Uncover
0 views • 42 slides
Understanding Time Complexity in Algorithm Analysis
Explore the concept of time complexity in algorithm analysis, focusing on the efficiency of algorithms measured in terms of execution time and memory usage. Learn about different complexities such as constant time, linear, logarithmic, and exponential, as well as the importance of time complexity co
0 views • 73 slides
Understanding Complexity in Polynomial Time: MAJORITY-3SAT and Related Problems
Dive into the world of MAJORITY-3SAT and its related problems, exploring the complexity of CNF formulas and the satisfiability of assignments. Discover the intricacies of solving canonical NP-complete problems and the significance of variables in determining computational complexity.
3 views • 35 slides
Sorting Techniques: Complexity, Stability, and Cases
This content discusses various sorting techniques, their time complexity in worst, best, and average cases, stability, and types of sorts. It includes a comparison table listing algorithms such as Bubble Sort, Selection Sort, Insertion Sort, Quick Sort, and more, along with their respective complexi
0 views • 10 slides
Understanding the MECE Framework for Efficient Problem-Solving
The MECE (Mutually Exclusive, Collectively Exhaustive) framework is a powerful tool used by business leaders and consultants like McKinsey to structure information, reduce complexity, and gather comprehensive data without overlaps. It involves creating issue trees that subdivide problem elements int
1 views • 4 slides
Exploring Complexity in Computational Theory
Dive into a world of computational complexity and theory with a focus on topics such as NP, P, PH, PSPACE, NL, L, random vs. deterministic algorithms, and the interplay of time and space complexity. Discover insights on lower bounds, randomness, expanders, noise removal, and the intriguing question
0 views • 17 slides
Quantum Query Complexity Measures for Symmetric Functions
Explore the relationships between query complexity measures, including quantum query complexity, adversary bounds, and spectral sensitivity, in the context of symmetric functions. Analysis includes sensitivity graphs, the quantum query model, and approximate counting methods. Results cover spectral
0 views • 19 slides
Exploring Proof Complexity: The Basics, Achievements, and Challenges
Delve into the intricacies of proof complexity, covering propositional, algebraic, and semi-algebraic proof systems, lower bound methods, and algorithmic implications. Discover fundamental connections to complexity theory and open problems in the field.
0 views • 76 slides
Developing Effective Reading Work Samples
Creating reading work samples involves steps like identifying a topic, analyzing passages, drafting tasks, formatting, administering, scoring, and revising tasks. Considerations include text complexity, high student interest, and grade-level appropriateness. Text complexity is assessed quantitativel
0 views • 15 slides
Additive Combinatorics Approach to Log-Rank Conjecture in Communication Complexity
This research explores an additive combinatorics approach to the log-rank conjecture in communication complexity, addressing the maximum total bits sent on worst-case inputs and known bounds. It discusses the Polynomial Freiman-Ruzsa Conjecture and Approximate Duality, highlighting technical contrib
0 views • 9 slides
Overview of Computational Complexity Theory: Savitch's Theorem, PSPACE, and NL-Completeness
This lecture delves into Savitch's theorem, the complexity classes PSPACE and NL, and their completeness. It explores the relationship between time and space complexity, configuration graphs of Turing machines, and how non-deterministic space relates to deterministic time. The concept of configurati
0 views • 67 slides
Exploring Circuit Size Bounds in Complexity Theory
The article delves into Shannon's Theorem in Complexity Theory, discussing the upper bounds of circuit sizes for Boolean functions of n variables. It explores the 1-1 correspondence with 0-1 strings of length 2n and how Boolean functions can be expressed as CNF or DNF formulas. The computation of th
2 views • 19 slides
Achieving Sublinear Complexity in Dynamic Networks
This research explores achieving sublinear complexity under constant ? in dynamic networks with ?-interval updates. It covers aspects like network settings, communication models, fundamental problems considered, existing results, and challenges in reducing complexity. The focus is on count time comp
0 views • 14 slides
Enhancing Spectrum Efficiency with Low Complexity Erasure Codes in IEEE 802.11 Document
This document delves into the implementation of erasure codes for content channels in IEEE 802.11 systems. By utilizing erasure codes, spectrum efficiency can be boosted without significantly increasing the complexity of encoding and decoding processes. The discussion also covers the duplication of
0 views • 20 slides
Introduction to NP-Completeness and Complexity Theory
Explore the concepts of NP-completeness, reductions, and the complexity classes P and NP in computational complexity theory. Learn about decision problems, Boolean functions, languages, polynomial-time Turing machines, and examples of problems in class P. Understand how to deal with functional probl
0 views • 56 slides
Understanding Complexity in Data Structures
Introduction to logarithms, fractional exponents, and complexity analysis in algorithms. Exploring Big O notation to express algorithm complexity and examples demonstrating different time complexities. Learn about the importance of analyzing the efficiency of algorithms in data structures.
0 views • 79 slides
Insights into Computational Complexity Hierarchy and SAT Algorithms
The computational complexity hierarchy explores classes of problems like EXP-complete, PSPACE-complete, and more. SAT algorithms, such as local search methods and survey propagation, offer new insights into practical complexity. Discover the interplay between tractable and intractable structures in
0 views • 12 slides
Understanding Complexity Theory in C++
Delve into the world of Complexity Theory with Cynthia Bailey Lee's peer instruction materials on P/NP definitions, decision vs. optimization problems, and the concept of O(2^n) time complexity. Explore the distinctions between problems in P and NP sets, grasp the implications of problem-solving spe
0 views • 27 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
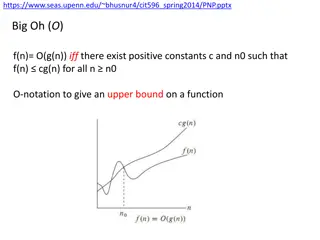
Understanding Big-Oh Notation in Time Complexity Analysis
Big-Oh notation in algorithm analysis signifies how the runtime of an algorithm grows in relation to the input size. It abstractly characterizes the worst-case time complexity, disregarding constants and lower-order terms. The concept of Big-Oh, along with Big-Omega and Big-Theta, helps in comparing
0 views • 18 slides
Insights into Polynomials Vanishing on Cartesian Products and the 3POL Problem
This joint work explores polynomials vanishing on Cartesian products, focusing on the 3POL problem involving three sets of points and a 6-variate polynomial. It discusses the running time of solving the explicit 3POL problem and compares it to the well-studied 3SUM problem in theoretical computer sc
0 views • 29 slides
Text Complexity and Reading Strategies in Education Sessions - June 7, 2012
Explore the engagement with text complexity and effective reading strategies in an educational workshop conducted on June 7, 2012. Delve into discussions on understanding text complexity levels, using margin notes and graphic organizers, and sharing key takeaways. Reflect on the challenges U.S. stud
0 views • 10 slides
Oracle Turing Machines in Computational Complexity Theory
The lecture delves into the concept of Oracle Turing Machines and their role in proving computational complexity results, such as the limitations of diagonalization in demonstrating P vs. NP. Oracle Turing Machines are defined as Turing Machines with access to a special query tape and states for ora
0 views • 59 slides
Managing Complexity in Health & Care Systems
Addressing the challenges of complexity in health and care systems, this content delves into embracing complexity, working in complex environments, and understanding the emergent nature of complex systems. It highlights the importance of being human, continuous learning, and nurturing healthy system
0 views • 28 slides
Understanding Text Complexity in Science and Literacy Education
Exploring the concept of text complexity beyond the familiar realm of Oz, this presentation delves into quantitative and qualitative measures, reader and task considerations, and steps to assess text complexity. Various resources and examples are provided to help educators gauge and improve the comp
0 views • 43 slides
Holographic Complexity in Hybrid De Sitter Spacetime
The research delves into holographic complexity in a hybrid de Sitter spacetime, exploring the AdS/CFT correspondence, quantum information in the bulk, and computational complexity. It also examines the volume of the ERB, evolution of complexity in CFT, and probes cosmological horizons using hologra
0 views • 12 slides
Complexity and Institutional Evolution in Economics
This paper explores the relevance of complexity theory in studying economic institutional evolution, focusing on the concepts of cumulative causation, increasing returns, and hierarchical emergence. It discusses the dynamic and computational complexity theories, highlighting the role of systems foll
0 views • 24 slides
Understanding Bounded Arithmetic and Definable Functions in Complexity Theory
Bounded arithmetic, as explored in complexity theory, focuses on theories like PA but with restrictions on formulas. The comprehension axiom determines sets that can exist, and TC is a first-order arithmetic theory defining functions within a specific complexity class. The witnessing theorem in TC e
0 views • 16 slides
Understanding Decision Problems in P and NP Complexity Classes
Decision problems play a crucial role in the realm of computational complexity theory, defining questions with binary answers that form the basis of the P and NP classes. This article delves into the significance of polynomial-time algorithms, distinguishes between tractable and intractable problems
0 views • 32 slides
Evaluating Interpretability in Machine Learning: Understanding Human-Simulatability Complexity
The paper discusses evaluating interpretability in Machine Learning by examining human-simulatability complexity and the relationship between decision set complexity and interpretability. It explores different factors affecting interpretability through user studies and highlights the significance of
0 views • 41 slides
Depth-Three Boolean Circuits and Arithmetic Circuits: A Study on Circuit Complexity
Explore the intricacies of depth-three Boolean circuits and arithmetic circuits with general gates, focusing on the size, structure, and complexity measures. The research delves into the relationship between circuit depth, gate types, and multi-linear functions, offering insights into circuit models
0 views • 12 slides
Understanding Complexity Measures of Boolean Functions
This work delves into the intricate world of complexity measures for Boolean functions, exploring concepts such as certificate complexity, decision tree depth, sensitivity, block sensitivity, PRAM complexity, and more. It sheds light on the relationships among different complexity measures and provi
0 views • 36 slides
Improved Merlin-Arthur Protocols for Fine-Grained Complexity Problems
The text discusses Merlin-Arthur proof systems and protocols for central problems in fine-grained complexity, particularly focusing on the time complexity, completeness, and soundness of these protocols. It also touches on recent interest in these protocols and presents new results in areas such as
0 views • 16 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Understanding QMA(2): Hamiltonians, Provers, and Complexity Classes
Exploring the complexities of QMA(2) through discussions on separable sparse Hamiltonians, the power of Merlin in L.QMA, the impact of prover restrictions on complexity classes like IP and MIP, and the difference between Merlin.A, Merlin.B, and Arthur in L.QMA(2). Delve into short proofs for NP-Comp
0 views • 27 slides
Challenges in Software Development: Understanding the Complexity
Society's dependence on software is increasing, yet many major software projects fail due to factors like late delivery, budget overruns, and changing requirements. Development challenges arise from the inherent complexity of software systems, human factors, and the need for creativity in solving ne
0 views • 30 slides
Orthogonal Vectors Conjecture and Sparse Graph Properties Workshop
Exploring the computational complexity of low-polynomial-time problems, this workshop delves into the Orthogonal Vectors Problem and its conjectures. It introduces concepts like the Sparse OV Problem, first-order graph properties, and model checking in graphs. Discussing the hardness of problems rel
2 views • 22 slides
Understanding PSPACE-Complete Problems in Complexity Theory
This content delves into complexity theory, exploring PSPACE-complete problems and their relevance within the realm of theoretical computer science. It covers concepts such as time complexity classes, P vs. NP dilemma, NP-complete languages, space complexity, PSPACE vs. NPSPACE, and PSPACE completen
1 views • 19 slides
Understanding NP-Complete Problems and Reductions
Exploring the realm of complexity theory, this topic delves into NP-complete problems and various types of reductions. From the Cook-Levin Theorem to the P vs. NP question, it navigates through the intricacies of computational complexity, time complexity classes, and the concept of reducibility in r
0 views • 38 slides
Understanding Big O Notation and Problem Complexity
Big O notation, Omega notation, and Theta notation are used in algorithm analysis to describe upper and lower bounds on functions. They help determine the efficiency and complexity of algorithms in terms of time and space. The content also covers examples of common computational problems like sortin
0 views • 39 slides