Understanding the Formulation of Hypothesis and Research Problem Definition
Research problems arise from situations requiring solutions, faced by individuals, groups, organizations, or society. Researchers define research problems through questions or issues they aim to answer or solve. Various sources such as intuitions, research studies, brainstorming sessions, and consul
5 views • 25 slides
Physics Chapter 27 Practice Problems
The chapter 27 problems involve concepts related to current, drift speed of electrons, current density, resistance, resistivity, temperature effects on resistance, and power calculations. The problems cover scenarios such as cathode ray tubes, aluminum wires, gold wires, tungsten wires, conductor re
0 views • 12 slides
Overview of APRN Regulation and Practice in Oklahoma
This content delves into the regulation and practice of Advanced Practice Registered Nurses (APRNs) in Oklahoma. It covers who regulates nursing practice, the roles and populations of APRNs, examination of laws related to CNP practice, approved certifications for APRN licensure, and updated legislat
0 views • 33 slides
Advanced Clinical Practice Framework and Pillars of Practice
The document discusses the advanced clinical practice framework and the four pillars of practice which include leadership & management, clinical practice, education, and research. It emphasizes the importance of core capabilities and area-specific competence in advanced clinical practice. The role o
2 views • 8 slides
Understanding The Simplex Method for Linear Programming
The simplex method is an algebraic procedure used to solve linear programming problems by maximizing or minimizing an objective function subject to certain constraints. This method is essential for dealing with real-life problems involving multiple variables and finding optimal solutions. The proces
0 views • 56 slides
Linear Programming Models for Product-Mix Problems and LP Problem Solutions
This unit covers the formulation of linear programming (LP) models for product-mix problems, including graphical and simplex methods for solving LP problems along with the concept of duality. It also delves into transportation problems, offering insights into LP problem resolution techniques.
0 views • 137 slides
Learning Objectives in Mathematics Education
The learning objectives in this mathematics course include identifying key words, translating sentences into mathematical equations, and developing problem-solving strategies. Students will solve word problems involving relationships between numbers, geometric problems with perimeter, percentage and
0 views • 30 slides
Integrating Nursing Research into Clinical Practice with Systems Thinking
Dr. Molly Secor-Turner emphasizes the importance of evidence-based practice (EBP) in nursing. EBP, derived from rigorous research, leads to quality patient outcomes by aligning services with current knowledge. The process involves identifying problems, critiquing evidence, implementing recommendatio
0 views • 21 slides
Introduction to Mathematical Programming and Optimization Problems
In optimization problems, one aims to maximize or minimize an objective based on input variables subject to constraints. This involves mathematical programming where functions and relationships define the objective and constraints. Linear, integer, and quadratic programs represent different types of
0 views • 25 slides
Examples of Optimization Problems Solved Using LINGO Software
This content provides examples of optimization problems solved using LINGO software. It includes problems such as job assignments to machines, finding optimal solutions, and solving knapsack problems. Detailed models, constraints, and solutions are illustrated with images. Optimization techniques an
1 views • 41 slides
Formulation of Linear Programming Problems in Decision Making
Linear Programming is a mathematical technique used to optimize resource allocation and achieve specific objectives in decision-making. The nature of Linear Programming problems includes product-mix and blending problems, with components like decision variables and constraints. Various terminologies
1 views • 14 slides
Weekly Skills Practice: 3rd Grade Math Problems - Week of May 11, 2020
This weekly skills practice for 3rd-grade math covers various topics such as determining the number of pencils in a store, calculating the total pages in a book, finding the total number of stickers, dividing items equally among people, determining the price of items, solving time-related questions,
0 views • 7 slides
Understanding Optimization Techniques for Design Problems
Explore the basic components of optimization problems, such as objective functions, constraints, and global vs. local optima. Learn about single vs. multiple objective functions and constrained vs. unconstrained optimization problems. Dive into the statement of optimization problems and the concept
0 views • 96 slides
Decimal Word Problems for Math Practice
Practice solving decimal word problems involving addition, subtraction, and basic calculations. The problems include scenarios like calculating distances, making purchases, and exploring number patterns with decimals. Get ready to sharpen your math skills with these engaging exercises and challenges
0 views • 6 slides
Solving Work Problems with Rational Equations
Learn how to solve work problems involving rational equations. Find the least common denominator, multiply by it, and solve for the variables. Practice examples like determining how long it takes workers to finish a task when working together. Also, solve distance equals rate times time problems to
0 views • 7 slides
Physics Practice Problems: Wheels, Rotations, and Acceleration
Explore a series of physics practice problems related to wheels, rotations, angular velocity, tangential velocity, and acceleration. Dive into scenarios involving bicycles, skateboards, hard drives, and cars to test your understanding of these concepts. From calculating linear distances traveled to
0 views • 36 slides
Engaging Mathematics Problems for Critical Thinking and Fun Learning
Explore a collection of engaging mathematics problems and classical brain teasers that challenge students to think critically, problem-solve creatively, and have fun while learning. From dissection tasks to card dealing challenges, these problems encourage students to readjust, reformulate, and exte
0 views • 36 slides
Algorithm Design Techniques: Divide and Conquer
Algorithm design techniques such as divide and conquer, dynamic programming, and greedy algorithms are essential for solving complex problems by breaking them down into smaller sub-problems and combining their solutions. Divide and conquer involves breaking a problem into unrelated sub-problems, sol
1 views • 13 slides
Understanding and Treating Sleep Problems in Children with Autism
Sleep problems in children with autism are viewed as skill deficits that can be addressed through relevant skills teaching. Good sleep is crucial for children's overall well-being, as it affects mood, behavior, learning, and physical health. Lack of good sleep can lead to irritability, fatigue, unin
0 views • 75 slides
Computational Complexity and NP-Complete Problems
In today's discussion, we delved into computational complexity and the challenges faced in finding efficient algorithms for various problems. We explored how some problems defy easy categorization and resist polynomial-time solutions. The concept of NP-complete problems was also introduced, highligh
0 views • 38 slides
Automatically Generating Algebra Problems: A Computer-Assisted Approach
Computer-assisted refinement in problem generation involves creating algebraic problems similar to a given proof problem by beginning with natural generalizations and user-driven fine-tuning. This process is useful for high school teachers to provide varied practice examples, assignments, and examin
0 views • 16 slides
Understanding Practice Drift in Nursing: Risks and Consequences
Explore the concept of practice drift in nursing, where nurses may deviate from standards leading to unsafe practice. Learn how to identify and prevent practice drift, understand scope of practice, and adhere to state regulations. Discover the importance of following the Model Nurse Practice Act and
0 views • 35 slides
Fermi Problems and Estimation Techniques in Science
Understand Enrico Fermi's approach to problem-solving through estimation in science as demonstrated by Fermi Problems. These problems involve making educated guesses to reach approximate answers, fostering creativity, critical thinking, and estimation skills. Explore the application of Fermi Problem
0 views • 23 slides
Fun With Numbers Activities and Practice Problems
Engage in fun learning activities related to numbers, including setting up graphic organizers, solving equations, and exploring interesting facts. Practice multiplying and dividing integers with examples provided. Test your skills with practice problems and check your answers. Have fun while learnin
0 views • 34 slides
Greedy Algorithms and Optimization Problems Overview
A comprehensive overview of greedy algorithms and optimization problems, covering topics such as the knapsack problem, job scheduling, and Huffman coding. Greedy methods for optimization problems are discussed, along with variations of the knapsack problem and key strategies for solving these proble
0 views • 17 slides
Understanding Signatures, Commitments, and Zero-Knowledge in Lattice Problems
Explore the intricacies of lattice problems such as Learning With Errors (LWE) and Short Integer Solution (SIS), and their relation to the Knapsack Problem. Delve into the hardness of these problems and their applications in building secure cryptographic schemes based on polynomial rings and lattice
0 views • 44 slides
Understanding Decision Problems in Polynomial Time Complexity
Decision problems play a crucial role in computational complexity theory, especially in the context of P and NP classes. These problems involve questions with yes or no answers, where the input describes specific instances. By focusing on polynomial-time algorithms, we explore the distinction betwee
0 views • 32 slides
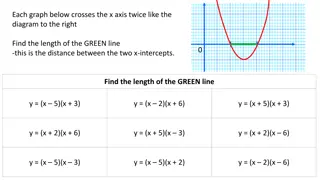
Mathematical Problems Involving Graphs and Equations
The content includes a set of mathematical problems related to graphs, equations, and modeling of paths using given equations. These problems involve finding distances, heights, and intersection points based on the provided graph representations. The scenarios involve water sprinklers watering lawns
0 views • 6 slides
Understanding Constraint Satisfaction Problems and Search
Constraint Satisfaction Problems (CSPs) involve assigning values to variables while adhering to constraints. CSPs are a special case of generic search problems where the state is defined by variables with possible values, and the goal is a consistent assignment. Map coloring is a classic example ill
0 views • 34 slides
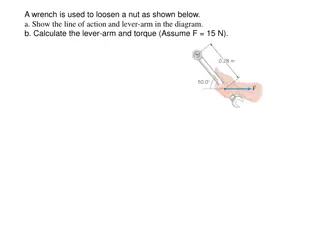
Physics Practice Problems and Analysis
In these physics problems, find the line of action and lever-arm of a wrench, calculate torque and angular acceleration of a motorcycle wheel, determine the velocity of a rolling ball using conservation of energy, solve equilibrium problems with balance beams, and analyze the forces exerted during p
0 views • 5 slides
Theory of Computation: Decidability and Encoding in CSE 105 Class
Explore the concepts of decidability, encoding, and computational problems in CSE 105 Theory of Computation class. Learn about decision problems, encodings for Turing Machines, framing problems as languages of strings, and examples of computational problems and their encodings. Gain insights into th
0 views • 26 slides
Model-Based Analysis for Identifying Operative Problems at Lelystad Airport
This research study presented at the International Conference on Air Transport 2015 explores the identification of operative problems at Lelystad Airport using a model-based approach. The study aims to develop a model for assessing the future performance of the airport, addressing challenges, and ob
0 views • 27 slides
Surgency as a Person-Level Risk Marker for Externalizing Problems in Children
Surgency is identified as a key interactive risk marker for externalizing problems in children, including Oppositional-Defiant Disorder (ODD) and Attention-Deficit/Hyperactivity Disorder (ADHD). This study explores how high surgency levels, when combined with low effortful control or low A, may incr
0 views • 23 slides
Python_constraint: Solving CSP Problems in Python
Python_constraint is a powerful package for solving Constraint Satisfaction Problems (CSP) in Python. It provides a simple yet effective way to define variables, domains, and constraints for various problems such as magic squares, map coloring, and Sudoku puzzles. This tool offers easy installation
0 views • 21 slides
Unit 1 Lesson 5 Practice Problems
This content includes practice problems for Unit 1 Lesson 5. The provided images contain multiple slides with various math exercises to help students practice and reinforce concepts covered in the lesson. These problems cover a range of topics and are designed to test comprehension and problem-solvi
0 views • 6 slides
Insights into NP-Hard Problems in Molecular Biology and Genetics
Understanding the complexity of NP-Hard Problems arising in molecular biology and genetics is crucial. These problems involve genome sequencing, global alignment of multiple genomes, identifying relations through genome comparison, discovering dysregulated pathways in human diseases, and finding spe
0 views • 24 slides
Understanding P, NP, NP-Hard, NP-Complete Problems and Amortized Analysis
This comprehensive study covers P, NP, NP-Hard, NP-Complete Problems, and Amortized Analysis, including examples and concepts like Reduction, Vertex Cover, Max-Clique, 3-SAT, and Hamiltonian Cycle. It delves into Polynomial versus Non-Polynomial problems, outlining the difficulties and unsolvability
0 views • 32 slides
Understanding NP-Hard Problems and NP-Completeness
Delve into the complexities of NP-hard problems, NP-complete problems, and the relationships between NP, NP-hard, and NP-complete classes. Learn about easy-to-verify problems in NP, the concept of NP-completeness, the first NP-complete problem - Gates Circuits, and the NP-complete problem CIRCUIT-SA
0 views • 15 slides
Equilibrium and Acid-Base Problems in Chemistry Lecture
In this lecture, topics such as Advanced Equilibrium, Acid/Base Equilibria, Systematic Method for solving chemical problems, Strong Acid/Strong Base scenarios, and General Comments on reactions are discussed. Examples using the systematic method are provided for practical understanding. Key points o
0 views • 13 slides
Evolution of Sociological Perspectives on Social Problems
The study of social problems has evolved dramatically since the 1970s, shifting from an objectivist approach to a more subjective and constructionist perspective. This shift acknowledges that what is considered a social problem is a matter of definition, and focuses on the social processes involved
0 views • 12 slides