Efficiency of Algorithms and Approximations
Efficiency of algorithms can be approximated using Big-O, Big-Omega, and Big-Theta notations, facilitating the evaluation of computer program performance. Real functions can be categorized based on their order with respect to other functions, enabling the determination of performance characteristics
10 views • 20 slides
Binomial Experiments and Probability Calculations
Binomial experiments have specific conditions to be met, such as fixed trials and two outcomes. Symbols and notations help represent these experiments. Calculating probabilities of successes in trials involves using functions like binompdf and binomcdf. Examples like determining defective switches o
11 views • 8 slides
Fundamentals of Stack Applications in Computer Science
Understanding the various applications of stacks in computer science is crucial for developing efficient algorithms. From balanced delimiters to postfix expressions, stacks play a key role in organizing and processing data efficiently. The provided examples demonstrate how stacks are utilized in sou
0 views • 14 slides
Math Set Notations and Probability Practice
Practice set notation and probability with quizzes on set notation, Venn diagrams, and probability calculations based on survey results. Improve your math skills through visual exercises and calculations.
2 views • 19 slides
High-Level Conceptual Data Modeling in Database Management Systems
Explore the world of high-level conceptual data modeling in database management systems through understanding ER and UML notations, designing entity-relationship models, and translating conceptual designs into practical implementation phases. Learn about data requirements analysis, database schema d
1 views • 79 slides
Crystal Structures: Unit Cell Definition and Wigner-Seitz Method
Learn essential concepts such as drawing Wigner-Seitz cells, identifying lattice directions, using direction/plane notations, locating directions/planes, and calculating distances in cubic or orthorhombic lattices. Explore various ways to define a unit cell within a lattice, including the Wigner-Sei
1 views • 25 slides
Challenges in Nuclear Data Program Evaluation and Remedies
Exploring evaluation challenges in a nuclear data program, including issues with decay cases and ambiguous notations. Remedies such as redesignating levels and clarifying decay probabilities are discussed to address these challenges.
0 views • 7 slides
Discourse Intonation in English Language Teaching
Discourse Intonation (DI) in English language teaching focuses on the significance of intonation in conveying meaning within spoken discourse. It involves key components such as prominence, tone, key, and termination. DI can help students and teachers by providing a framework for analyzing intonatio
0 views • 11 slides
Evolution of Musical Notation Systems and Contexts
Explore the diverse world of musical notation systems, from Eastern to Western traditions, spanning Babylonian notations, Guido d'Arezzo's contributions, Gregorian chants, and modern-day tempo measures. Uncover the rich history and nuances of musical expression through various scales, staves, orname
0 views • 12 slides
Music Progression of Learning at Hailey CE Primary School - National Curriculum Overview
The music progression of learning at Hailey CE Primary School includes key objectives for Key Stage 1 and Key Stage 2 pupils. Students are taught to use their voices expressively, play instruments, listen to various music types, experiment with sound, play and perform in solo or ensemble settings, i
1 views • 6 slides
Optical Security with Double Random Fractional Fourier Domain Encoding
Utilizing double random fractional Fourier domain encoding for optical security involves encryption and decryption methods based on the fractional Fourier transform of various orders, involving specific mathematical operations and notations. The process includes transforming the input function, encr
0 views • 13 slides
Functional Architecture Design and Data Flow Diagrams in Industrial Information Systems
The chapter delves into the fundamentals of structured analysis techniques such as data flow diagrams and structured analysis and design technique. It emphasizes the graphical notations used for depicting information flows within enterprise processes. Different methodologies like IDEF0 and SADT are
1 views • 20 slides
Symmetric Chromatic Function for Voltage Graphs
Exploring the concept of a Symmetric Chromatic Function (SCF) for voltage graphs involves proper coloring conditions for edges and vertices, edge polarization functions, and decomposing voltage graphs into disconnected and connected squiggly graphs. The SCF allows for determining the number of ways
0 views • 7 slides
Introduction to Analysis Methods of Proof
This content introduces various methods of proof in analysis, including direct proof, counterexamples, and indirect proofs like contrapositive. It covers common notations, sets, symbols, implications, theorems, and examples with analyses. The goal is to understand how to prove or disprove theorems u
0 views • 22 slides
Introduction to Methods of Proof in Mathematics
Explore the methods of proof in mathematics through direct and indirect proofs, common symbols, set notations, and theorems. Learn how to prove or disprove statements using logical reasoning and examples. Enhance your understanding of mathematical reasoning and application in various problem-solving
1 views • 24 slides
Divide & Conquer Approach to Model Checking
Addressing the state space explosion issue in model checking, this work by Canh Minh Do, Yati Phyo, and Kazuhiro Ogata introduces a divide & conquer approach focusing on until and until stable properties. The research extends techniques to handle these properties effectively, emphasizing mitigation
3 views • 17 slides
Journey Through Math Education: From Sea Level to High School
Exploring the progression of mathematical concepts from grade 8 sea level to high school, this journey covers functions, patterns, linear regression, and geometric functions. Students transition through various levels, deepening their understanding and application of mathematical concepts with each
0 views • 13 slides
Finite-time Analysis of the Multiarmed Bandit Problem in Advanced Algorithms Seminar
This study delves into the Stochastic Multiarmed Bandit Problem and explores achieving logarithmic regret uniformly over time. It covers problem settings, notations, previous work, objectives, results, and proofs, including the usage of the UCB1 policy. The theorem and its proof demonstrate the expe
1 views • 43 slides
Concurrent Broadcast for Information Dissemination
Concurrent broadcast facilitates the efficient dissemination of information across network nodes through message contention and transmission. This method finds applications in adaptive routing and communication networks, aiding in the collection and distribution of global network status information
0 views • 21 slides
Basic Geometrical Ideas in Geometry
Basic Geometrical Ideas in Geometry cover the fundamental concepts of points, lines, and planes. Points are described as having location but no size, lines are infinite sets of points, and collinearity is discussed. The importance of straightness in lines is assumed but not defined. Symbols and nota
1 views • 45 slides
Electronic Configurations Through Simplified Assignments
Exploring electron configurations and orbital regions using simplified notations colored in on Periodic Charts. Descriptions and visual aids for Carbon, Fluorine, and excited state of Fluorine. Learn to assign s, p, d, and f electron neighborhoods without memorization through a fun song. Includes te
1 views • 14 slides
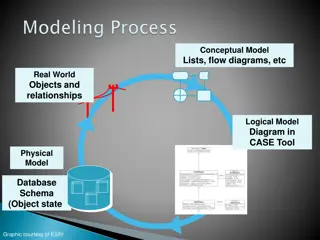
Data Modeling and Database Schema Design
Explore various aspects of data modeling, ranging from conceptual to physical models, using tools like CASE Tool and ArcGIS. Learn about entity-relationship diagrams, UML notations, and diagrammatic notations in the context of constructing data models. Discover the significance of classes, relations
0 views • 20 slides
Language Change and Sound Evolution
Explore the processes and examples of language change, including sound alterations, observed notations, reconstruction methods, and the regularity of sound changes. Discover how linguists analyze conditioned changes, assimilation, and the neogrammarian model to track linguistic evolution.
1 views • 31 slides
Basic Principles of Inheritance in Information Systems
Understanding inheritance in information systems is crucial for designing efficient architectures. This chapter delves into the principles of inheritance, such as attribute and method inheritance, generalization, and subtype hierarchies. It also discusses the modeling of inheritance through UML nota
0 views • 71 slides
EHR System Function and Information Model: Manage Allergy, Intolerance, and Adverse Reactions
This document outlines the function to manage patient-specific allergy, intolerance, and adverse reaction lists in an Electronic Health Record system. It covers capturing, maintaining, and viewing allergen information over time, including patient-reported events and provider-verified notations. The
0 views • 13 slides
Innovative Practices in Special Education Music Classes
Explore a new session format focusing on sharing best practices in special education music classes. From enlisting your EAs to preparing instruments and music sheets, this guide offers alternative notations and creative presentation ideas. Get inspired by practical tips and strategies for engaging s
0 views • 31 slides
Automatic Decoder Synthesis: Advancements in Communication and Cryptography
Cutting-edge progress in automatic decoder synthesis for communication and cryptography systems, presented in a comprehensive study covering motivation, prior work, preliminary notations, SAT solver algorithms, and experimental findings.
0 views • 32 slides
Boolean Algebra: Predicates and Quantifiers in CSE 311 Spring '22 Lecture 5
Dive into the world of Boolean Algebra with this comprehensive guide that explores the fundamentals of predicates, quantifiers, and their applications in computer science and circuit design. Discover the concepts behind Boolean variables, logical operations, and equivalence in Propositional Logic. E
1 views • 52 slides
Differential Equations and Boundary Value Problems
Explore the world of Differential Equations (DE) with a focus on Boundary Value Problems, guided by Dennis G. Zill and Michael R. Cullen. Dive into the realm of First Order and Higher Order DE, Partial DE, Laplace Transform, Fourier Series, and more. Unravel the complexities of DE through various se
0 views • 33 slides
New Rules for Domain-Independent Lifted MAP Inference
In this work by Happy Mittal and team at IIT Delhi, new rules for domain-independent lifted MAP inference are introduced. The study covers motivations, notations, preliminaries, and two main rules. Markov Logic Networks (MLN) are discussed along with examples illustrating friendship, smoking habits,
0 views • 56 slides
Essential Parts of Business Letters
In the realm of business communication, understanding the vital components of a well-crafted letter is crucial. Learn about attention lines, subject lines, reference initials, attachment/enclosure notations, copy notations, blind copy notations, and second-page headings. Master the nuances that enha
0 views • 8 slides
Big-O Notation in Algorithms
Big-O notation is a crucial method to describe algorithm complexity in terms of time or space. This notation provides an estimate of the steps needed for algorithm completion and helps in analyzing algorithm efficiency. Explore examples and rules to grasp the implications of different complexities l
0 views • 7 slides
Examples of List Comprehensions and Notations
This content provides examples and explanations of list comprehensions, mathematical notations, ways to convert Centigrade to Fahrenheit, syntax, semantics, and types of comprehensions. It covers topics such as expressing lists, mathematical sets, and efficient Python techniques. Learn how to easily
0 views • 14 slides
Asymptotic Series: Properties and Notations
Asymptotic series play a crucial role in analyzing functions as their magnitude grows. Explore the properties and notations of asymptotic series, including Big O and Small o notations. Learn how these series show the behavior of functions as their input values increase.
0 views • 39 slides
Understanding UML - Types of Diagrams, Notations, and Hierarchies
Learn about UML (Universal Modeling Language) and its significance in software design. Explore different types of diagrams such as class, object, use case, and more. Gain insights into notations for classes, objects, inheritance, and states in UML. Understand the hierarchy of UML elements and discov
0 views • 14 slides
Legal Informatics and Communication: Prelingual Codes and Formal Notations
Explore the intersection of legal informatics, human and machine communication through prelingual codes, formal notations, and language. Understand how these elements shape interactions between animals, humans, and machines in various contexts.
0 views • 8 slides
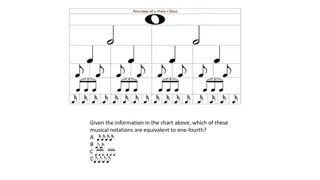
Musical Notations, Candy Sales, Student Demographics, Monthly Expenses, Pizza Fraction, Sound Travel Calculation
Explore various math problems involving musical notations, candy sales percentages, student demographics, monthly expenses breakdown, fractions, and sound travel calculations. Answer questions on equivalent musical notations, sold candy percentages, gender distribution, color percentages, favorite m
0 views • 13 slides
Understanding Data Structures and Algorithms: Basics, Textbook, Grading, and Notations
Discover the fundamental concepts of data structures and algorithms, including definitions, recommended textbooks, grading breakdown, and helpful notations for analyzing algorithms such as Big-O, Big-Omega, and Big-Theta. Learn about formal algorithm definitions and how to analyze pseudo-code effect
0 views • 20 slides
Understanding Asymptotic Notations in Algorithms
Learn about major asymptotic notations like Big-O, Big-Omega, Theta, small-o, small-omega, and how they are used to analyze the running time of algorithms based on different growth rates. Explore practical examples and comparisons to enhance your understanding.
0 views • 18 slides
Understanding Asymptotic Notations for Algorithm Complexity Analysis
Learn about asymptotic notations such as Big Theta, Big O, and Big Omega to analyze the running time of algorithms in relation to input size. Explore how these notations describe the rate of growth of functions and establish bounds for algorithm efficiency.
0 views • 36 slides