Portfolio Matrix: Strategic Product Positioning Guide
Learn about the Portfolio Matrix, a strategic tool assessing products based on industry growth and market share. Explore the BCG matrix, its four categories, and how it guides decision-making for products' future success.
1 views • 14 slides
The Importance of Completing a Trainer Matrix
Completing a Trainer Matrix is essential for Registered Training Organizations (RTOs) to demonstrate compliance with Standards for RTOs 2015, specifically Clauses 1.13 to 1.16. This matrix outlines requirements for trainers, including holding relevant qualifications, industry skills, and maintaining
2 views • 38 slides
Eisenhower Matrix for Efficient Task Prioritization
Use the Eisenhower Matrix template to effectively prioritize project tasks by distinguishing between urgent and important activities. Delegate, delete, or tackle tasks based on their significance for optimal time management. An example matrix provided showcases various tasks categorized as urgent/im
2 views • 4 slides
Interlock Actions and Matrix for DSS Server in SR1 Environment
Proposal and implementation plan for interlock actions and matrix coordination between DSS server rack and user areas in SR1. Includes agreements, alarms-actions matrix finalization, cable routing, server installation, and commissioning with dummy loads. Discusses CO2 plant signals, temperature moni
5 views • 7 slides
Governance Decision Authorities Matrix Overview
A Governance Decision Authorities Matrix is a crucial tool that articulates roles and responsibilities for major decision-making within a system. This template provides a starting point for customizing governance structures, focusing on areas like fiduciary responsibilities, strategic planning, qual
3 views • 9 slides
Singular Value Decomposition and the Conjugate Gradient Method
Singular Value Decomposition (SVD) is a powerful method that decomposes a matrix into orthogonal matrices and diagonal matrices. It helps in understanding the range, rank, nullity, and goal of matrix transformations. The method involves decomposing a matrix into basis vectors that span its range, id
0 views • 21 slides
Intervention Planning Matrix for Enhanced Learning Support
Enhance learning support with the Intervention Planning Matrix tool developed by the Healthy Wisconsin Leadership Institute. This tool helps brainstorm strategies for impactful policy changes and community interventions. Utilize the tips provided to maximize the effectiveness of the tool, and engage
0 views • 7 slides
Linear Algebra Review for Big Data Summer Institute
Join Rupam Bhattacharyya at the Big Data Summer Institute for a comprehensive review of linear algebra concepts. Explore topics such as matrix notation, special matrices, shapes of matrices, and matrix operations. Gain valuable insights for applications in big data analysis and machine learning.
0 views • 18 slides
Diagonalization in Linear Algebra
Discover the concept of diagonalization in linear algebra through eigenvectors, eigenvalues, and diagonal matrices. Learn the conditions for a matrix to be diagonalizable, the importance of eigenvectors in forming an invertible matrix, and the step-by-step process to diagonalize a matrix by finding
0 views • 26 slides
Advancements in Quantum Systems Techniques for Density Matrix Minimization
Discover the innovative methods and applications of open quantum systems techniques for density matrix minimization. Explore the motivation behind the research, early developments, purification processes, linear scaling potentials, Bloch's method intricacies, quantum channel algorithms, canonical de
0 views • 22 slides
Matrix Factorization for Latent Factor Recovery
Explore the concept of matrix factorization for recovering latent factors in a matrix, specifically focusing on user ratings of movies. This technique involves decomposing a matrix into multiple matrices to extract hidden patterns and relationships. The process is crucial for tasks like image denois
0 views • 50 slides
Improved Rectangular Matrix Multiplication Using Coppersmith-Winograd Tensor
In this research, the complexity of rectangular matrix multiplication is enhanced by analyzing the fourth power of the Coppersmith-Winograd tensor. By extending the understanding of the tensor's power, significant advancements have been made in the efficiency of non-square matrix multiplication, sur
0 views • 25 slides
Linear Equations and Matrix Operations
Explore the concepts of linear equations, matrix forms, determinants, and finding solutions for variables like x1, x2, x3. Learn about Cramer's Rules, Adjoint Matrix, and calculating the inverse of a matrix through examples and formulas.
0 views • 24 slides
Evolution of Musical Notation Systems and Contexts
Explore the diverse world of musical notation systems, from Eastern to Western traditions, spanning Babylonian notations, Guido d'Arezzo's contributions, Gregorian chants, and modern-day tempo measures. Uncover the rich history and nuances of musical expression through various scales, staves, orname
0 views • 12 slides
Chemistry Exam Review: Topics in Scientific Notation, Molecular Weight, Stoichiometry, and Limiting Yield
Explore key concepts in chemistry, including scientific notation, molecular weight calculations, reaction balancing, stoichiometry, and limiting yield problems. Prepare for an upcoming exam by practicing various problems and conversions related to these topics, such as expressing numbers in scientif
0 views • 4 slides
Tooth Numbering Systems in Dentistry
Dental professionals use various tooth numbering systems to identify and record teeth in the mouth. The three main systems are Universal Notation, Zsigmondy/Palmer Notation, and Federation Dentaire Internationale (FDI). Universal Notation utilizes letters for primary teeth and numbers for permanent
0 views • 19 slides
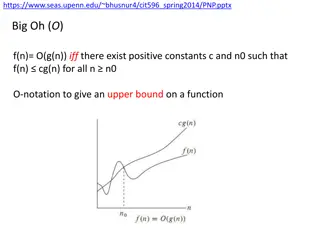
Big-Oh Notation in Time Complexity Analysis
Big-Oh notation in algorithm analysis signifies how the runtime of an algorithm grows in relation to the input size. It abstractly characterizes the worst-case time complexity, disregarding constants and lower-order terms. The concept of Big-Oh, along with Big-Omega and Big-Theta, helps in comparing
0 views • 18 slides
Global Matrix 4.0 Spanish Report Card Leaders Meeting Overview
The Global Matrix 4.0 Spanish Report Card Leaders Meeting provides insights into national and regional report cards, introduction of Spanish leaders, and discussions on national coordination and future opportunities for various regions. The meeting aims to harmonize messaging, share information, and
0 views • 9 slides
Advanced Circuit Simulation Using Matrix Exponential Operators
Explore the innovative approach of circuit simulation via matrix exponential operators as proposed by CK Cheng from UC San Diego. The method involves utilizing general matrix exponentials, Krylov spaces, Arnoldi orthonormalization, and inverting Krylov subspaces for accurate simulations. These techn
0 views • 28 slides
Multiple Regression Analysis of Energy Consumption in Luxury Hotels - Hainan Province, China
Conducting a multiple regression analysis on the energy consumption of luxury hotels in Hainan Province, China using matrix form in Excel. The dataset includes 19 luxury hotels with the dependent variable being energy consumption (1M kWh) and predictors such as area, age, and effective number of gue
0 views • 13 slides
Revolutionizing Hotel Communication with Matrix Hospitality Solution
Simplify hotel operations and enhance guest experiences with Matrix Hospitality Solution. From enhancing staff efficiency to boosting revenue generation opportunities, Matrix offers a comprehensive suite of features to meet the diverse needs of hotels. Its modular configuration, scalable platform, a
1 views • 36 slides
Matrix Measurements and Analysis After First Metal Workshop
The pilot run matrix measurements were conducted following the 7th Belle II VXD workshop and the 18th International Workshop on DEPFET Detectors and Applications by Rainer H. Richter and Paola Avella for the MPP/HLL team. The measurements included assessing defects, diode integrity, metal shorts, an
0 views • 30 slides
Composite Matrix Materials in Engineering
Composite materials are made of reinforcing fibers and matrix materials, with the matrix serving to protect and enhance the properties of the composite. There are three main types of composite matrix materials: metal matrix composites (MMC), ceramic matrix composites (CMC), and polymer matrix compos
0 views • 22 slides
Music Notation and Interpretation in KS3 Curriculum
Explore music notation in KS3 Music curriculum, focusing on reading and writing notes from E up to F on the treble clef. Understand various forms of notation such as graphic scores and enhance your musical literacy skills throughout the academic year.
0 views • 89 slides
Scientific Notation and SI Measurement Basics
Explore scientific notation as a method for expressing large and small numbers efficiently in mathematical calculations. Practice converting numbers into scientific notation and learn the rules for multiplication, division, addition, and subtraction in this format. Additionally, discover the benefit
0 views • 41 slides
Creating Effective Expectation Matrix for School Environment
Engage in a structured activity to develop behavior guidelines using an expectation matrix. Follow guidelines to positively state rules, keep them concise, and focus on desired behaviors. Utilize sticky notes to define specific rules per setting and location. Gather insights to build a schoolwide be
0 views • 5 slides
Scientific Notation in Mathematics and Chemistry
Scientific notation is an essential concept for representing very large or very small numbers efficiently. It simplifies numbers by expressing them as a coefficient multiplied by a power of 10. This summary covers the basics of scientific notation, from converting numbers to and from scientific nota
0 views • 55 slides
Matrix Functions and Taylor Series in Mathematics
A detailed exploration of functions of matrices, including exponential of a matrix, eigenvector sets, eigenvalues, Jordan-Canonical form, and applications of Taylor series to compute matrix functions like cosine. The content provides a deep dive into spectral mapping, eigenvalues, eigenvectors, and
0 views • 53 slides
Understanding a Bus Matrix Analytics in Power BI
A bus matrix is a two-dimensional visualization in Power BI that shows the intersection of facts (additive amounts) and dimensions (descriptive attributes), enabling relationships between data fields. This concept is crucial for running cross-process analysis efficiently. Star-schema examples demons
0 views • 5 slides
Parallel Computation for Matrix Multiplication
Matrix multiplication is a fundamental operation with diverse applications across scientific research. Parallel computation for matrix multiplication involves distributing the computational workload over multiple processors, improving efficiency. Different algorithms have been developed for multiply
0 views • 36 slides
Exponents: Simplifying Expressions and Scientific Notation
Explore the concept of exponents, learn how to simplify expressions with negative exponents, and delve into scientific notation for efficiently representing large numbers. Discover the basics of exponents, operations involving exponents, and the application of scientific notation in various discipli
0 views • 8 slides
Scientific Notation: Converting, Multiplying, Dividing & More
Scientific notation is a way to express large or small numbers efficiently. Learn how to convert numbers to and from scientific notation, multiply and divide in scientific notation, and ensure proper formatting. Understand the rules for exponents and make calculations easier with these simple steps.
0 views • 8 slides
Scientific Notation and Conversions
Scientific notation is a useful way to express very large or very small numbers in a concise form. This chapter discusses how to convert numbers between scientific notation and decimal notation, providing examples and explanations for better understanding.
0 views • 18 slides
Exponents and Scientific Notation
Exponents are powers to which bases are raised, allowing for efficient representation and calculation of numbers. This review covers the basics of exponents, rules, laws, and practical applications. Scientific notation offers a method to express very large or small numbers using powers of 10. Learn
0 views • 13 slides
Set Notation and Probability in Visuals
Explore the concepts of vocabulary, set notation, Venn diagrams, probability, experiments, outcomes, sample space, events, unions, intersections, complements, and set notation through visual aids and clear explanations. Learn about subsets, empty sets, and more in this comprehensive resource from Wa
0 views • 24 slides
Matrix Video Surveillance Solution for Retail - Enhancing Security and Productivity
Matrix offers a comprehensive video surveillance solution for retail businesses, enhancing security and productivity. Their real-time security features help trace customer belongings and deter theft. Additionally, their productivity solutions aid in managing heavy customer flow, ensuring employee di
0 views • 14 slides
Monitoring Matrix on Enabling Environment for Civil Society Development - Insights and Perspectives
Explore insights from a partners workshop in Prishtina, Kosovo, discussing the value and relevance of the Monitoring Matrix exercise for civil society development. Learn about research beyond the Matrix, respondent engagement, and ideal implementation scenarios.
0 views • 24 slides
Big O Notation and Problem Complexity
Big O notation, Omega notation, and Theta notation are used in algorithm analysis to describe upper and lower bounds on functions. They help determine the efficiency and complexity of algorithms in terms of time and space. The content also covers examples of common computational problems like sortin
0 views • 39 slides
Scientific Notation
Explore the world of scientific notation through a series of examples and explanations. Understand how to convert large numbers into scientific notation and vice versa, as well as the significance of the placement of the decimal point. Dive into scenarios where exponents play a crucial role in repre
0 views • 10 slides
Scientific Notation Operations
World of scientific notation through multiplication, division, and comparison of celestial objects like Jupiter and Mercury. Learn to simplify expressions, utilize associative properties, and calculate the mass differences between planets. Get familiar with expressing results in scientific notation
0 views • 13 slides