Understanding Interpolation and Pulse Shaping in Real-Time Digital Signal Processing
Discrete-to-continuous conversion, interpolation, pulse shaping techniques, and data conversion in real-time digital signal processing are discussed in this content. Topics include types of pulse shapes, sampling, continuous signal approximation, interpolation methods, and data conversion processes
4 views • 14 slides
Understanding Surfaces and Interfacial Energy in Chemistry
Surfaces play a crucial role in free energy and dissolution processes, impacting surface tension and interfacial energy. Learn about the adsorption of molecules, surface excess properties, and the contributions of surface area and curvature to surface energy. Dive into concepts such as Laplace's equ
6 views • 71 slides
Understanding H.264/AVC: Key Concepts and Features
Exploring the fundamentals of MPEG-4 Part 10, also known as H.264/AVC, this overview delves into the codec flow, macroblocks, slices, profiles, reference picture management, inter prediction techniques, motion vector compensation, and intra prediction methods used in this advanced video compression
3 views • 32 slides
Approaches for Approximating Non-Linear Equations
Techniques for approximating solutions to non-linear algebraic equations involve converting the problem into a root-finding one. Seven methods such as Newton's method, bisection method, and linear interpolation are utilized with specific halting conditions. Tangent and secant lines, as well as Taylo
2 views • 13 slides
Understanding Laplace Interpolation for Sparse Data Restoration
Laplace Interpolation is a method used in CSE 5400 by Joy Moore for interpolating sparse data points. It involves concepts such as the mean value property, handling boundary conditions, and using the A-times method. The process replaces missing data points with a designated value and approximates in
1 views • 13 slides
Laplace's Nebular Hypothesis: Origin of the Solar System
French mathematician Laplace proposed the nebular hypothesis in 1796, refining Kant's gaseous hypothesis. Laplace asserted a hot rotating gaseous nebula cooled gradually, contracting and increasing rotation speed. Eventually, centrifugal forces led to the formation of ring structures, contrasting wi
0 views • 6 slides
Understanding Curve Fitting Techniques
Curve fitting involves approximating function values using regression and interpolation. Regression aims to find a curve that closely matches target function values, while interpolation approximates points on a function using nearby data. This chapter covers least squares regression for fitting a st
0 views • 48 slides
Understanding Interpolation Techniques in Computer Analysis & Visualization
Explore the concepts of interpolation and curve fitting in computer analysis and visualization. Learn about linear regression, polynomial regression, and multiple variable regression. Dive into linear interpolation techniques and see how to apply them in Python using numpy. Uncover the basics of fin
3 views • 44 slides
Introduction to Differential Equations and Laplace Equations
Understanding differential equations of various orders, solving methods, linear and non-linear equations, ordinary and partial differential equations, definitions of solutions, and general vs. particular solutions in the context of Differential Equations and Laplace Equations.
1 views • 20 slides
Understanding Numerical Methods and Errors in Computation
Delve into the world of numerical methods through the guidance of Dr. M. Mohamed Surputheen. Explore topics such as solving algebraic and transcendental equations, simultaneous linear algebraic equations, interpolation, numerical integration, and solving ordinary differential equations. Learn about
0 views • 130 slides
Understanding Probability: Theory and Examples
Explore the concepts of probability through the classical theory introduced by Pierre-Simon Laplace in the 18th century. Learn about assigning probabilities to outcomes, the uniform distribution, and calculating probabilities of events using examples like coin flipping and biased dice rolls.
1 views • 14 slides
Digital Differential Analyzer (DDA) Algorithm in Computer Graphics
In computer graphics, the Digital Differential Analyzer (DDA) Algorithm is utilized as the basic line drawing algorithm. This method involves interpolation of variables between two endpoints to rasterize lines, triangles, and polygons efficiently. The algorithm requires inputting coordinates of two
0 views • 9 slides
Understanding Interpolation in Numerical Methods
Interpolation is a fundamental mathematical operation used in numerical methods to find the value of a function between known data points. It involves computing the value of a function at any point within a given interval based on existing data. Newton's forward interpolation formula is commonly use
0 views • 18 slides
Understanding Curl-Free and Div-Free Radial Basis Functions in Physical Situations
This content explores the applications of Curl-Free and Div-Free Radial Basis Functions in solving partial differential equations for fields, the theoretical soundness of using RBFs, and examples illustrating divergence-free interpolation. It also delves into matrix-valued RBF formulations, converge
3 views • 13 slides
Understanding Spatial Autocorrelation in Geostatistical Analysis
Explore the concept of spatial autocorrelation, its implications in geostatistical analysis, and the importance of detecting and interpreting it correctly. Learn about auto-correlation, signal components, correlation significance, and measuring autocorrelation using tools like Moran's I. Gain insigh
0 views • 12 slides
Technical Training Instruction Set for Mathematics
Explore a comprehensive technical training instruction set for mathematics, including operations like decrement, increment, linear interpolation, extrapolation, and complex calculations. Dive into the details of each operation's parameters and behaviors, along with practical examples and editing fun
0 views • 15 slides
Understanding Laplace Transform in Mathematical Modeling
Explore the concept of Laplace Transform in mathematical modeling through equations and physical interpretations. Learn how this tool helps in reconstructing functions using exponentials. Practice and patience are key to mastering these subtle ideas.
1 views • 17 slides
Understanding Quaternaries in Semiconductor Nanodevice Design
Learn about the treatment of quaternary materials in semiconductor nanodevice simulations, including material parameters needed for GaAs/AlGaAs heterostructures and interpolation techniques for ternaries. Explore the complexities of AlxGa1-xAsyP1-y and AlxGa1-xIn1-x-yAs quaternaries, along with the
0 views • 10 slides
Understanding Interpolation Techniques for Synthetic Aperture Radar (SAR) Implementation
Dive into the world of Synthetic Aperture Radar (SAR) implementation tools and techniques, including resampling methods, interpolation of band-limited signals, and the analysis of SAR-specific algorithms like range Doppler and chirp scaling. Explore how resampling algorithms enable non-uniform sampl
0 views • 35 slides
Understanding Matrix Algebra for Solving Systems of Equations
Explore the application of matrix algebra in solving systems of equations through a practical example involving the interpolation of rocket velocity data. Learn how to set up equations in matrix form to find the coefficients profile of the velocity polynomial, illustrating the concept effectively.
0 views • 71 slides
Exploring Additive Manufacturing: A Revolutionary Technology
Additive manufacturing, commonly known as 3D printing, has witnessed significant advancements since its inception in the 1980s. This technology allows for the creation of three-dimensional objects through various processes like extrusion, binding, and polymerization. With the rise of accessible 3D p
3 views • 14 slides
Effective Data Augmentation with Projection for Distillation
Data augmentation plays a crucial role in knowledge distillation processes, enhancing model performance by generating diverse training data. Techniques such as token replacement, representation interpolation, and rich semantics are explored in the context of improving image classifier performance. T
0 views • 13 slides
Understanding Language Modeling in Human Language Technologies
Exploring the concepts of language modeling in human language technologies, this presentation delves into N-grams, the chain rule of probability, evaluation metrics like perplexity, smoothing techniques such as Laplace, and the goal of assigning probabilities to sentences. It covers applications lik
1 views • 81 slides
Understanding Bayes Rule and Its Historical Significance
Bayes Rule, a fundamental theorem in statistics, helps in updating probabilities based on new information. This rule involves reallocating credibility between possible states given prior knowledge and new data. The theorem was posthumously published by Thomas Bayes and has had a profound impact on s
0 views • 34 slides
An Lp Theory for Outer Measures: Application to Singular Integrals II
This discussion covers various topics such as tents (or Carleson boxes), outer measures on the open upper half-plane, sizes of functions on tents, outer essential supremum on subsets, outer Lp spaces, embedding theorems, and estimates related to Linfity-Sinfty and weak L1-Sinfty. The content delves
0 views • 34 slides
Nonlinear Curve Fitting Techniques in Engineering
Utilizing nonlinear curve fitting techniques is crucial in engineering to analyze data relationships that are not linear. This involves transforming nonlinear equations into linear form for regression analysis, as demonstrated in examples and methods such as polynomial interpolation and exponential
0 views • 18 slides
ALMA Observation of Ceres Surface Temperature
ALMA conducted ground-based observations of Ceres' surface temperature providing valuable insights for planetary science. The data processing steps involved models interpolation, radio calibration, and thermal gradient correction to produce thermal flux maps. Key objectives included detecting the ed
0 views • 9 slides
Understanding Zero-Shot Adversarial Robustness for Large-Scale Models
Pretrained large-scale vision-language models like CLIP show strong generalization on unseen tasks but are vulnerable to imperceptible adversarial perturbations. This work delves into adapting these models for zero-shot transferability in adversarial robustness, even without specific training on unk
0 views • 18 slides
Enhancing Precipitation Interpolation Methods for High-Resolution Data Analysis
Accurate interpolation of precipitation data is crucial for various applications, especially in regions with limited data coverage like Greece. This study focuses on improving the creation of a precipitation atlas for Greece using daily observation analysis. By analyzing the reliability of the metho
0 views • 24 slides
Discussion on RadD and Other Questions in Physics
This discussion revolves around suggestions for improvements in the RadD code related to Physics, such as providing a Makefile, combining data structures, simplifying user input, and considering interpolation techniques. The conversation also addresses changes in the ALPHAD program for calculating h
0 views • 14 slides
Understanding Laplace Transforms for Continuous Random Variables
The Laplace transform is introduced as a generating function for common continuous random variables, complementing the z-transform for discrete ones. By using the Laplace transform, complex evaluations become simplified, making it easy to analyze different types of transforms. The transform of a con
0 views • 17 slides
Understanding Interpolation Methods in Physics
Interpolation in physics involves constructing a function that fits known data points to estimate values at arbitrary points. It is a method to fill in data gaps and is a specific case of curve fitting. Linear interpolation and polynomial interpolation are common methods used in this process, each w
0 views • 18 slides
Hypotheses on the Origin of Earth and Earth's Formation
Various materialist hypotheses proposed by scientists such as Kant, Laplace, Schmidt, and Fesenkov regarding the origin of Earth and the solar system. These hypotheses suggest different processes, including the formation from primary dusty matter, hot nebula, interstellar meteorite dust, and gas-dus
0 views • 16 slides
Quasi-Interpolation for Scattered Data in High Dimensions: Methods and Applications
This research explores the use of quasi-interpolation techniques to approximate functions from scattered data points in high dimensions. It discusses the interpretation of Moving Least Squares (MLS) for direct pointwise approximation of differential operators, handling singularities, and improving a
0 views • 9 slides
Exploring Methods for Evaluating Matrix Exponential
This study delves into various techniques for evaluating the matrix exponential, including the Cauchy Integral Formula and Putzer's equation via Laplace Transforms. Motivated by linear ordinary differential equations, the matrix exponential is explored in depth, showcasing its applications and signi
0 views • 23 slides
Bayes’ Rule
Bayes Rule, a fundamental concept in statistics, explores how prior beliefs are updated based on new evidence. This rule, named after Thomas Bayes, has had a profound impact on statistical inference and has been further developed by mathematicians like Laplace. Exploring the probabilistic reasoning
0 views • 34 slides
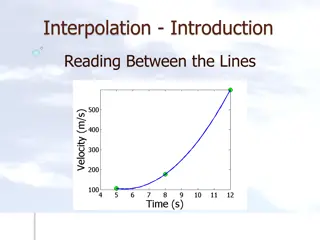
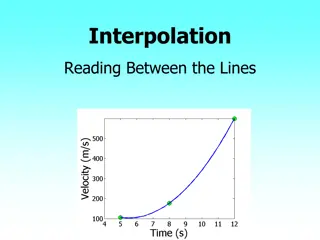
Understanding Interpolation: Reading Data Patterns & Solving Practical Problems
Explore the concept of interpolation through real-world examples like predicting values between data points and solving problems like rocket velocity calculation and heat transfer. Dive into understanding specific heat of carbon, thermistor calibration, and spline method of interpolation. Learn to f
0 views • 45 slides
Understanding Interpolation: Methods and Applications
Interpolation is a technique used to estimate values between known data points. This content covers the concept of interpolation, its applications in solving real-world problems like rocket velocity and specific heat calculations, and methods such as spline interpolation. Explore how interpolation h
0 views • 42 slides
Understanding Differential Equations and Boundary Value Problems
Explore the world of Differential Equations (DE) with a focus on Boundary Value Problems, guided by Dennis G. Zill and Michael R. Cullen. Dive into the realm of First Order and Higher Order DE, Partial DE, Laplace Transform, Fourier Series, and more. Unravel the complexities of DE through various se
0 views • 33 slides
Fast and Efficient MPM Solver for Strain Localization Problems
This study presents a fast and efficient Material Point Method (MPM) solver for strain localization problems, introducing the Generalized Interpolation Material Point Method (GIMPM) and Convected Particle Domain Interpolation (CPDI). The MPM computational phase involves mapping, nodal solution, and
0 views • 19 slides