The Semantic Argument for the Existence of God - International Conference Insights
Explore the Semantic Argument and its implications for the existence of God as presented by Emanuel Rutten at the International Proofs of God's Existence Conference. The lecture delves into universal properties, formal versus non-formal properties, and the likelihood of God's existence based on thes
0 views • 14 slides
COMPSCI 330: Design and Analysis of Algorithms
Logistics for COMPSCI 330 include lecture and recitation schedules, grading breakdown, exam conflicts, contact information, and lecture format. Dr. Rong Ge emphasizes hands-on learning through proofs and recording lectures. The course covers algorithm basics such as divide and conquer, dynamic progr
1 views • 20 slides
Exploring FAEST: Post-Quantum Signatures and Zero-Knowledge Proofs
Delve into the world of FAEST, a post-quantum signature scheme, with a focus on publicly verifiable zero-knowledge proofs. The presentation covers VOLE-in-the-Head, families of ZK proofs, and the application of VOLE in creating VOLE-ZK proofs. Learn about the background of VOLE, its use in the desig
1 views • 26 slides
Understanding Greedy Algorithms and Minimum Spanning Trees
Greedy algorithms build solutions by considering objects one at a time using simple rules, while Minimum Spanning Trees find the most cost-effective way to connect vertices in a weighted graph. Greedy algorithms can be powerful, but their correctness relies on subtle proofs and careful implementatio
6 views • 61 slides
Discrete Mathematics
Explore the foundations of logic and proofs in discrete mathematics, focusing on compound propositions, bit operations, and applications of propositional logic. Learn about how computers use bits for information representation and manipulation, and delve into translating English sentences into logic
5 views • 15 slides
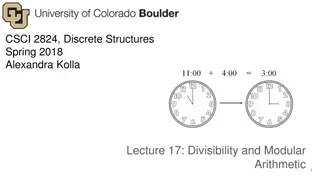
Understanding Divisibility and Modular Arithmetic in Discrete Structures
This lecture discusses the concepts of divisibility and modular arithmetic in the context of discrete structures. It covers definitions, notation, and examples of divisibility by integers, including proving properties such as the divisibility of products and consecutive integers. Through practical e
1 views • 43 slides
Explore Latin and Greek Root Words Unit 10: CRIMIN, CULP, ONER, ONUS, PROB, PROV
Delve into the meanings and uses of Latin and Greek root words in Unit 10, including terms like approbation, culpable, exonerate, onerous, recrimination, reprobate, and more. Understand concepts related to crime, blame, guilt, onus, burdens, and proofs through examples and explanations.
0 views • 9 slides
Understanding Latitude, Longitude, and Earth's Shape
Explore the concepts of latitude, longitude, and the shape of the Earth through informative content. Discover the significance of the troposphere, continental crust density, and proofs that the Earth is round. Learn how latitude is measured, the role of Polaris (North Star), and how these elements i
2 views • 15 slides
Mathematical Definitions and Theorems Illustrated
In this collection of images, various mathematical concepts are visually presented, including definitions, theorems, and proofs. The slides cover a range of topics in a structured manner, providing a concise overview of key mathematical principles. From foundational definitions to detailed proofs, t
0 views • 12 slides
Understanding Indirect Proofs: Contradiction and Contraposition Examples
Indirect proofs offer a roundabout approach to proving statements, with argument by contradiction and argument by contraposition being the main techniques. Argument by contradiction involves supposing the statement is false and deriving a contradiction, while argument by contraposition relies on the
1 views • 18 slides
Understanding Algebraic Proofs and Equations
Explore algebraic proofs, equations solving techniques, and properties of equality through examples. Learn about the distributive property, temperature conversion, and problem-solving applications in algebra. Enhance your understanding of logic and algebraic reasoning.
0 views • 30 slides
Understanding Direct Proofs in Discrete Mathematics
Explore the principles of direct proof in discrete mathematics through a Peer Instruction approach by Dr. Cynthia Bailey Lee and Dr. Shachar Lovett. Learn how to prove theorems of the form "if p, then q" using logical rules, algebra, and math laws. Utilize a clear template for direct proofs, practic
0 views • 17 slides
Guide to Direct Proofs in Discrete Math
Dive into the world of direct proofs in discrete math with this comprehensive guide. Learn how to prove implications, create truth tables, and follow a step-by-step direct proof template. Test your understanding with engaging quizzes and practical examples. Master the art of logical reasoning and fo
0 views • 18 slides
Evolution of Proofs in Cryptography
Cryptography has evolved from classical proofs to interactive and probabilistically checkable proofs, enabling the development of applications like Non-Malleable and Chosen-Ciphertext Secure Encryption Schemes. Non-Malleability protects against active attacks like malleability and chosen-ciphertext
0 views • 29 slides
Post-Quantum Cryptography Security Proofs and Models Overview
Explore the various aspects of post-quantum cryptography security, including evaluation criteria, building public key cryptography (PKC) systems, security proofs, digital signatures, and reduction problems. Dive into topics such as performance, cryptanalysis, provable security, standard models, exis
0 views • 42 slides
Mathematical Proof Techniques and Examples
Explore various proof techniques in mathematics including direct proofs, proofs by cases, proofs by contrapositive, and examples showing how to prove statements using algebra, definitions, and known results. Dive into proofs involving integers, even and odd numbers, and more to enhance your understa
2 views • 13 slides
Practical Statistically-Sound Proofs of Exponentiation in Any Group
The paper presents practical and statistically sound proofs of exponentiation in any group. It discusses the computation process, applications in verifiable delay functions and time-efficient arguments for NP, as well as interactive protocols and the overview of PoEs. The research contributes a stat
0 views • 18 slides
Algebra and Geometry Reasoning: Concepts and Proofs
Explore key concepts in algebra and geometry reasoning, including properties of equality, distributive property, and proofs using deductive reasoning. Practice solving equations, identifying properties of congruence, and writing two-column proofs to justify mathematical statements.
0 views • 13 slides
Challenges in Constant-Round Public-Coin Zero-Knowledge Proofs
The paper discusses the implausibility of constant-round public-coin zero-knowledge proofs, exploring the limitations and complexities in achieving them. It delves into the fundamental problem of whether such proofs exist, the challenges in soundness error reduction, and the difficulties in parallel
0 views • 20 slides
Effective Learning Strategies for Mathematical Proof Comprehension
Explore self-explanation training techniques to enhance students' understanding of mathematical proofs. Dive into key concepts such as definitions, worked examples, theorems, and proofs, focusing on intuitive learning methods and practical applications.
0 views • 27 slides
Exploring Architecture and Challenges of Proof Assistants
Explore the architecture of proof assistants, discussing the use of tactics, formal proofs, and the difficulty in utilizing these tools. Discover the contribution of a new architecture for proof assistants, addressing extensibility and error checking, with a focus on soundness guarantees. Delve into
0 views • 41 slides
Towards Establishing Scientifically Valid Proofs for Mythological Cosmology by Bamidele Oluwade
This presentation by Bamidele Oluwade explores the research on mythological cosmology, aiming to provide scientifically valid proofs for metaphysical phenomena through mathematical models and standard methods of proof in mathematics, supported by scientific/thought experiments and results from vario
0 views • 45 slides
Undecidability Proofs and Reductions in Theory of Computation
Explore undecidability proofs and reductions in the context of Theory of Computation through examples and explanations. Understand how problems are reduced to show undecidability, with demonstrations involving Turing Machines and languages. Gain insights into proving statements like the undecidabili
0 views • 21 slides
Advancements in Interactive Proofs for Efficient Computation
Recent developments in interactive proofs focus on enhancing the efficiency of computations outsourced to untrusted servers, addressing concerns related to correctness and privacy. Solutions like doubly efficient interactive proofs offer a secure way to delegate computations while minimizing relianc
0 views • 25 slides
Understanding Exhaustive Proofs and Proof by Cases in Discrete Math
Exhaustive proofs and proofs by cases are essential methods in discrete mathematics for proving theorems. Exhaustive proofs involve checking all possibilities, while proof by cases focuses on considering different scenarios separately. The methods are illustrated through examples like proving (n+1)^
0 views • 8 slides
Understanding and Checking Mathematical Proofs
Reading and understanding mathematical proofs involves careful analysis of logic and reasoning. Mathematicians and students use various strategies to ensure correctness, such as examining assumptions, following step-by-step logic, and verifying conclusions. This process is crucial for grasping the v
1 views • 79 slides
Evolution of Proofs in Computer Science
Explore the development of proofs in computer science, from classical mathematical proofs to interactive and zero-knowledge proofs pioneered by researchers like Goldwasser, Micali, Rackoff, and others. Discover how proof theory has evolved over time, making computation verification more efficient an
0 views • 28 slides
Constant Round Interactive Proofs for Delegating Computations
The research explores techniques for securely delegating computations to the cloud, addressing concerns of correctness and privacy through interactive proofs and efficient verification methods. It compares classical and doubly efficient interactive proofs, emphasizing the importance of computational
0 views • 43 slides
Exploring Metamath: A Computer Language for Mathematical Proofs
Metamath is a computer language designed for representing mathematical proofs. With several verifiers and proof assistants, it aims to formalize modern mathematics using a simple foundation. The Metamath-100 project is focused on proving a list of 100 theorems, with significant progress made in prov
0 views • 17 slides
Evolution of Proofs in Computer Science: Zero-Knowledge Proofs Overview
Explore the evolution of proofs in computer science focusing on succinct zero-knowledge proofs, their significance, and impact on Bitcoin protocol and public ledgers. Learn about classical proofs, zero-knowledge proofs by Goldwasser-Micali-Rackoff, and interactive proofs in the realm of computer sci
0 views • 40 slides
Understanding Predicate Logic and Quantifiers for Symbolic Proofs
Dive into the realm of predicate logic and quantifiers, exploring the nuances of symbolic proofs and evaluating logical statements. Learn about bound variables, domain considerations, and strategies for constructing iron-clad proofs using quantifiers.
0 views • 36 slides
Quantum NIZK Proofs Explained with Dominique Unruh
Explore the concept of non-interactive quantum zero-knowledge proofs with Dominique Unruh at the University of Tartu. Discover how these proofs ensure verifier acceptance of true statements while learning nothing, and delve into the various implementations and implications of Quantum NIZK proofs wit
0 views • 19 slides
Zero-Knowledge Proofs in Cryptography
Exploring zero-knowledge proofs in cryptography, this content delves into interactive protocols, perfect zero-knowledge definitions, and the QR protocol's honest verifier and malicious verifier zero-knowledge theorems. It discusses how simulators work to maintain zero-knowledge properties and the si
0 views • 37 slides
Theorems on Convergent Sequences with Proofs and Examples
The lecture covers theorems on convergent sequences, including the convergence of monotonic increasing and decreasing sequences when bounded. Detailed proofs for these theorems are provided, along with examples to determine if a sequence is bounded. The presentation includes step-by-step explanation
0 views • 6 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
0 views • 40 slides
Predicate Logic and Proofs in CSE 311
Explore the translation of statements into predicate logic, learn about inference proofs and nested quantifiers, and delve into the application of logical thinking in real-world scenarios. Discover a new way of constructing proofs and understand notation laws of inference. Engage in interactive proo
0 views • 37 slides
Exploring NP-Completeness Proofs in Pencil Puzzles: The Case of Nondango
Delve into the realm of NP-Completeness proofs within pencil puzzles through the intriguing case of Nondango. Unravel the challenge of coloring circles in a rectangular grid to meet specific criteria, showcasing the complexity and depth of this puzzle type.
0 views • 40 slides
Logical Resolution Proofs and Exercise Solutions
This content provides exercises on logical resolution proofs and solutions, including proving that "West is a criminal" and resolving statements related to mortality, relationships, and more. It also covers converting statements to Conjunctive Normal Form (CNF).
0 views • 9 slides
Algebraic Complexity and Equational Proofs in Arithmetic Formulas
Explore the intricacies of polynomial identity testing (PIT), equational proofs, and arithmetic formulas in the context of algebraic complexity. Learn about the minimal number of operations needed to compute the zero polynomial and derive new identities using derivation rules and axioms in polynomia
0 views • 39 slides
Understanding Mathematical Proofs and Concepts
Explore the world of mathematical proofs through chapters 4, 5, and 6. Delve into terminology, theorems, definitions, divisors, and accepted axioms used in mathematical reasoning. Discover the logic behind proofs and various methods employed in establishing the truth of mathematical statements.
1 views • 101 slides