Understanding Increasing and Decreasing Functions
Discover the concept of increasing and decreasing functions, learn how to identify intervals of increase or decrease, and explore the relationship between gradients and function behavior. Dive into differentiation of polynomials and grasp the essence of proving a function's characteristics through analysis. Enhance your understanding with practical examples and graphical representations to master this fundamental aspect of calculus.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Increasing and Decreasing Functions Understand that some functions are increasing or decreasing over all or part their domain Find the values of x for which a function is increasing or decreasing Prove that a function is increasing or decreasing
Increasing & Decreasing Functions Look at how the value of the gradient changes as we move along this curve. At any given point the function is either increasing, decreasing or stationary.
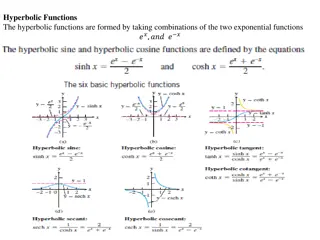
Increasing & Decreasing Functions A function can also be increasing and decreasing in certain intervals. 2,3 What do you think it means for a function to be an increasing function ? 4, 1 Increasing for ? 2 ? An increasing function is one whose gradient is always at least 0. ? ? 0 for all ?. Increasing for ? 4 ? Decreasing for 2 ? 4 ? We could also write ? ? is decreasing in the interval [2,4] [?,?] represents all the real numbers between ? and ? inclusive, i.e: ?,? = ? ? ? ? It would be strictly increasing if ? ? > 0 for all ?, i.e. is not allowed to go horizontal.
A function is said to be increasing when its gradient is positive. dy dx A function y = f(x) is increasing if 0. So: A function is said to be decreasing when its gradient is negative. dy dx 0. A function y = f(x) is decreasing if So: Is the function f(x) = x3 6x2 + 2 increasing or decreasing at the point where x = 3? f (x) = 3x2 12x f (3) = 27 36 = 9 The gradient is negative, so the function is decreasing.
Your Turn 1 2 3
Suppose we want to know the range of values over which a function is increasing or decreasing. For example: Find the range of values of x for which the function f(x) = x3 6x2 + 2 is decreasing. f (x) = 3x2 12x f(x) is decreasing when f (x) < 0. That is, when 3x2 12x < 0 x2 4x < 0 x(x 4)< 0 We can sketch the graph of y = x(x 4)to find the range for which this inequality is true.
Find the range of values of x for which the function f(x) = x3 6x2 + 2 is decreasing. The coefficient of x2 > 0 and so the graph will be -shaped. Also, the roots of y = x(x 4)are x = 0 and x = 4. This is enough information to sketch the graph. The inequality x(x 4)< 0 is true for the parts of the curve that lie below the x-axis. y y (4, 0) (4, 0) (0, 0) (0, 0) 0 0 x x So 0 < x < 4. f(x) = x3 6x2 + 2 therefore decreases for 0 < x < 4
Your Turn Show that the function ? ? = ?3+ 6?2+ 21? + 2 is increasing for all real values of ?. ? ? = 3?2+ 12? + 21 ? ? = 3 ?2+ 4? + 7 = 3 ? + 22+ 9 ? ? + 22 0 for all real ?, 3 ? + 22+ 9 0 for all real ? ?(?) is an increasing function for all ?. Tip: To show a quadratic is always positive, complete the square, then indicate the squared term is always at least 0.
Your Turn Find the interval on which the function ? ? = ?3+ 3?2 9? is decreasing. ? ? = ?3+ 3?2 9? ? ? = 3?2+ 6? 9 ? ? 0 3?2+ 6? 9 0 ?2+ 2? 3 0 ? + 3 ? 1 0 ? 3 ? 1 So ?(?) is decreasing in the interval [ 3,1]
Your Turn Show that the function ? ? = ?3+ 16? 2 is increasing for all real values of ?. Find the interval on which the function ? ? = ?3+ 6?2 135? is decreasing. ? ? = 3?2+ 12? 135 ? ? = 3?2+ 16 ? ? 0 ?2 0 for all real ? 3?2+ 12? 135 0 ?2+ 4? 45 0 ? + 9 ? 5 0 ? 3?2+ 16 0 for all real ?. ? Therefore ?(?) is an increasing function for all real ?. 9 ? 5 So ?(?) is decreasing in the interval [ 9,5]