Understanding Ratios and Proportions in Mathematics
Ratios are a fundamental concept in mathematics that compare the sizes of different quantities. This content explains how to find ratios between quantities, simplify ratios, and work with ratios expressed in different units or containing decimals. Understanding ratios and proportions is crucial for various mathematical applications. Visit www.mathssupport.org for in-depth insights and examples.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
16 September 2024 Ratio and proportion LO: To find the ratio between two quantities. www.mathssupport.org
Ratio A ratio compares the sizes of parts or quantities to each other. For example, What is the ratio of red stars to blue stars? red : blue = 9 : 3 = 3 : 1 For every three red stars there is one blue star. www.mathssupport.org
Ratio A ratio compares the sizes of parts or quantities to each other. For example, The ratio of blue counters to red counters is not the same as the ratio of red counters to blue counters. stars to red stars? What is the ratio of blue blue : red = 3 : 9 = 1 : 3 For every blue star there are three red stars. www.mathssupport.org
Ratio What is the ratio of red stars to yellow stars to blue stars? red : yellow : blue = 12 : 4 : 8 = 3 : 1 : 2 For every three red stars there is one yellow star and two blue stars. www.mathssupport.org
Simplifying ratios Ratios can be simplified by multiplying or dividing each part by the same non-zero number. For example, 21 : 35 7 7 = 3 : 5 For a three-part ratio all three parts must be divided by the same number. For example, 6 : 12 : 9 3 3 = 2 : 4 : 3 www.mathssupport.org
Simplifying ratios with units When a ratio is expressed in different units, we must write the ratio in the same units before simplifying. Simplify the ratio 90p : 3. First, write the ratio using the same units. 90p : 300p When the units are the same we can simplify them in the ratio. 90 : 300 30 30 = 3 : 10 www.mathssupport.org
Simplifying ratios with units Simplify the ratio 0.6 m : 30 cm : 450 mm. First, write the ratio using the same units. 60 cm : 30 cm : 45 cm 60 : 30 : 45 15 15 = 4 :2 : 3 www.mathssupport.org
Simplifying ratios containing decimals When a ratio is expressed using fractions or decimals we can simplify it by writing it in whole-number form. Simplify the ratio 0.8 : 2. We can write this ratio in whole-number form by multiplying both parts by 10. 0.8 : 2 10 10 = 8 : 20 4 4 = 2 : 5 www.mathssupport.org
Simplifying ratios containing fractions 2 3 Simplify the ratio : 4. We can write this ratio in whole-number form by multiplying both parts by 3. 2 3 : 4 3 3 = 2 : 12 2 2 = 1 : 6 www.mathssupport.org
Equal ratios Ratios are equal if they can be expressed in the same simplest form. For example, the ratio 6 : 4 can be written in the form 3 : 2 the ratio 9 : 6 can also be written in the form 3 : 2 so, they are equal ratios We can say: 6 : 4 = 9 : 6 A proportion is a statement that two ratios are equal. 6 : 4 = 9 : 6 is a proportion www.mathssupport.org
Proportions Sometimes we need to compare one quantity given the ratio and the other quantity. To do this we use equal ratios. For example, find x if: 3 : 5 = 6 : x = 6 : x 3 : 5 2 = 6 : x 6 : 10 x = 10 www.mathssupport.org
Proportions Example Find x if: 15 : 20 = x : 16 = x : 16 15 : 20 5 = x : 16 3 : 4 4 12 : 16 = x : 16 x = 12 www.mathssupport.org
Unitary method for ratios We can compare ratios by writing them in the form 1 : m, wheremis any number. For example, the ratio 5 : 8 can be written in the form 1 : m by dividing both parts of the ratio by 5. 5 : 8 5 5 = 1 : 1.6 The ratio 5 : 8 can also be written in the form n : 1 by dividing both parts of the ratio by 8. 5 : 8 8 8 = 0.625 : 1 www.mathssupport.org
Unitary method for ratios The ratio of boys to girls in class 9P is 4:5. The ratio of boys to girls in class 9G is 5:7. Which class has the higher proportion of girls? The ratio of boys to girls in 9P is 4 : 5 4 4 = 1 : 1.25 The ratio of boys to girls in 9G is 5 : 7 5 5 = 1 : 1.4 9G has a higher proportion of girls. www.mathssupport.org
Solving problems using Unitary ratio The ratio of Fatima s height to Hamed s height is 7 : 6. If Fatima is 1.63 m tall, how tall is Hamed? Fatima : Hamed Fatima : Hamed 7 : 6 7 : 6 7 7 1.63 : x 1 :6 1.63 : x x 1.63= 6 7 6 1.63 7 Writing the proportion 7 1.63 1.63 x 1.63 : 1.40 = Multiply both sides by 1.63 x = 1.40 www.mathssupport.org
Solving problems using Unitary ratio In one year Sofia s height increases from 150 cm in the ratio 31 : 30. Find Sofia s new height? The second number in the ratio represents the original quantity. The first number represents the final quantity New height : Original height New height : Original height 31 : 30 31 : 30 30 30 x : 150 31 30 x : 150 31 30 31 150 30 x : 1 Writing the proportion = 150 150 150 x 155 : 150 = Multiply both sides by 150 155 = x www.mathssupport.org
Solving problems using Unitary ratio On a particular day, 1 Australian dollar is worth 0.94 US dollars, How many Australian dollars can be exchanged for 20 US? Suppose $20 US is worth x Australian dollars Australian dollars : US dollars 1 : 0.94 x : 20 x 20 1 Writing the proportion = 0.94 20 0.94 Multiply both sides by 20 x = 21.28 = x www.mathssupport.org
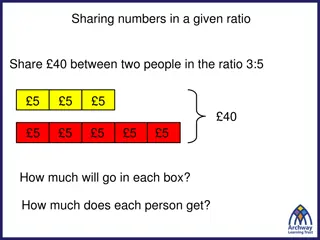
Dividing in a given ratio Divide 40 in the ratio 2 : 3. A ratio is made up of parts. We can write the ratio 2 : 3 as 2 parts : 3 parts The total number of parts is 2 parts + 3 parts = 5 parts We need to divide 40 by the total number of parts. 40 5 = 8 www.mathssupport.org www.mathssupport.org
Dividing in a given ratio Divide 40 in the ratio 2 : 3. Each part is worth 8 so 2 parts = 2 8 = 16 and 3 parts = 3 8 = 24 40 divided in the ratio 2 : 3 is 16 : 24 Always check that the parts add up to the original amount. 16 + 24 = 40 www.mathssupport.org www.mathssupport.org
Dividing in a given ratio A citrus twist cocktail contains orange juice, lemon juice and lime juice in the ratio 6 : 3 : 1. How much of each type of juice is contained in 750 ml of the cocktail? First, find the total number of parts in the ratio. 6 parts + 3 parts + 1 part = 10 parts Next, divide 750 ml by the total number of parts. 750 ml 10 = 75 ml www.mathssupport.org www.mathssupport.org
Dividing in a given ratio A citrus twist cocktail contains orange juice, lemon juice and lime juice in the ratio 6 : 3 : 1. How much of each type of juice is contained in 750 ml of the cocktail? Each part is worth 75 ml so, 6 parts of orange juice = 6 75 ml = 450 ml 3 parts of lemon juice = 3 75 ml = 225 ml 1 part of lime juice = 75 ml Check that the parts add up to 750 ml. 450 ml + 225 ml + 75 ml = 750 ml www.mathssupport.org www.mathssupport.org
Dividing in a given ratio Here it is a question that shows the two different types of ratio problem: Fruity Mix is made from concentrated fruit juices and water. The ingredients are apricot juice, apple juice, pineapple juice and water in the ratio 2 : 3 : 7 : 28. a)How much of each ingredient is used to make 240 litres of Fruity Mix? b)If 24 litres of apple juice are used, how much of the other ingredients are needed? www.mathssupport.org www.mathssupport.org
Dividing in a given ratio Fruity Mix is made from concentrated fruit juices and water. The ingredients are apricot juice, apple juice, pineapple juice and water in the ratio 2 : 3 : 7 : 28. a) How much of each ingredient is used to make 240 litres of Fruity Mix? Add the ratio 2 + 3 + 7 + 28 = 40 Divide into the quantity 240 40 = 6 Multiply the ratio: 2 x 6 : 3 x 6 : 7 x 6 : 28 x 6 12 litres : 18 litres : 42 litres : 168 litres Apricot : Apple : Pineapple : Water www.mathssupport.org www.mathssupport.org
Dividing in a given ratio Fruity Mix is made from concentrated fruit juices and water. The ingredients are apricot juice, apple juice, pineapple juice and water in the ratio 2 : 3 : 7 : 28. b) If 24 litres of apple juice are used, how much of the other ingredients are needed? Apricot : Apple : Pineapple : Water 2 : 3 : 7 : 28 : 24 : : 16 56 224 24 3 = 8 so 3 x 8 = 24 You multiply all the numbers by 8 www.mathssupport.org www.mathssupport.org
Thank you for using resources from A close up of a cage Description automatically generated For more resources visit our website https://www.mathssupport.org If you have a special request, drop us an email info@mathssupport.org Get 20% off in your next purchase from our website, just use this code when checkout: MSUPPORT_20 www.mathssupport.org