Polar Curves: Intersections, Areas, and Calculating Enclosed Areas
Explore polar curves, their intersections, areas enclosed by curves, and calculating enclosed areas using given equations. Learn to sketch graphs, find points of intersection, polar coordinates, and apply formulas for finding enclosed areas with examples provided.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
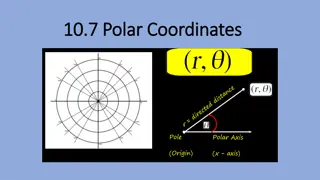
POLAR CURVES Intersections
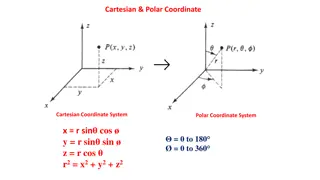
Polar curves KUS objectives BAT Find points of intersection of Polar curves BAT Find Areas bounded by parts of Polar curves Starter: Sketch these graphs: r = 4 cos ? = 10cos? ? =1 r = 2 sin 4 4sin? r = 1 + cos ? = 6cos? + 8sin? ? = ????? ? = ????? ? ? ? = ?????? ?2= ?2+ ?2
WB16 a) On the same diagram, sketch the curves with equations: ? = 3 + 2cos? and ? = 5 2cos? for ? ? ? b) Find the polar coordinates of the intersection of these curves To find the intersection, we can use the two equations we were given: 3 + 2???? = 5 2???? 2 = 4???? 0.5 = ???? ? =? 3, ? 3 Using these values of , we get r = 2.5 at both points
WB17 a) On the same diagram, sketch the curves with equations: r = 2 + cos and r = 5cos b) Find the polar coordinates of the intersection of these curves To find the intersection, we can use the two equations we were given: 2 + ???? = 5???? 2 2 = 4???? (2.5, /3) 0.5 = ???? ? =? 3, ? ? = ? + ???? 3 0, 2 Using these values of , we get r = 2.5 at both points ? = ????? (2.5,- /3) 3 2
POLAR CURVES Areas
WB18a To find the area enclosed by the curve, and the half lines = and = , you can use the formula : ???? =1 ? ?2 ?? 2 ? 2 Find the area enclosed by the curve, r = 1 + cos , and the half lines = and = 3 6 3, 6 ? 31 + ????2 ?? =1 2 ? 6 0, 2 notice the 1/2r2 being familiar as the formula for the area of a sector ? = ? + ???? 3 2
Find the area enclosed by the curve, r = 1 + cos, and the half lines = WB18b 6 and = 3, ? 31 + ????2 ?? ? 3(1 + 2cos? + ???2? )?? 1 2 ? =1 2 ? 6 6 ? 3(1 + 2cos? +1 =1 2 ? 2cos2? + 1 )?? 6 ? 3 3 =1 2+ 2cos? +1 2 ? 2cos2? ?? 6 ? 3 ? 6 =1 3 2? + 2sin? +1 2 4sin2? =1 3? 6+ 2sin? 3+1 4sin2? 3 1 3 2 ? 6+ 2sin? 6+1 4sin2? 2 2 6 = 1.047
WB19a Find the area enclosed by the cardioid with equation: r = a(1 + cos) As the curve has reflective symmetry, we can find the area above the x-axis, then double it 2 Sketch the graph (you won t always be asked to do this, but you should do as it helps visualise the question ) So for this question: 0 0, 2 ? = ?(1 + ????) ? = 0 ? = ? We will now substitute these into the formula for the area, given earlier: 3 2 ? 2 ?? ?? 1 + ???? ???? =1 = 0 ?2 ?? 2 ? ? = ?2 1 + 2???? + ???2? ?? 0 We will need to rewrite the cos2 term so we can integrate it ?3 2+ 2???? +1 ?1 + 2???? +1 2???2? +1 = ?2 =?2 0 2???2? ?? 2 ?? 0 Now we can think about actually Integrating!
WB19b Find the area enclosed by the cardioid with equation: r = a(1 + cos) ?3 2+ 2???? +1 = ?2 2???2? ?? 0 ? 3 2? + 2???? +1 = ?2 4???2? 0 3 2? + 0 + 0 0 + 0 + 0 = ?2 = 3??2 2 Show full workings, even if it takes a while. It is very easy to make mistakes here!
WB20a Find the area of one loop of the curve with polar equation : r = asin4 From the patterns you have seen, you might recognise that this will have 4 loops Think about plotting r = asin4 1 0 Sin /2 3 /2 2 -1 From the Sine graph, you can see that r will be positive between 0 and As the graph repeats, r will also be positive between 2 and 3 , 4 and 5 , and 6 and 7 So we would plot r for the following ranges of 4 2 4 3 4 4 5 0 4 6 4 7 0 /4 /2 3 /4 5 /4 3 /2 7 /4 So the values we need to use for one loop are: /2 /4 3 /4 Sometimes it helps to plot the limits for positive values of r on your diagram! ? =? ? = ????4? ? = 0 4 0 7 /4 5 /4 3 /2
WB20b Find the area of one loop of the curve with polar equation : r = asin4 ? 4????4?2 ?? ? 4?2???24? ?? ? ???? =1 1 2 0 1 2 = ?2 ?? 2 ? 0 ? 4???24? ?? We will need to write sin24 so that we can integrate it 1 2?2 0 ? 41 ???8??? 1 4?2 0 Now this has been set up, we can actually Integrate it! ? 4 1 4?2? 1 1 4?2? 8???8? 0 =??2 16 4 1 Important points: 8???2? You sometimes have to do a lot of rearranging/substitution before you can Integrate Your calculator might not give you exact values, so you need to find them yourself by manipulating the fractions
WB21a a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves 2 a) And b) were done in WB 17 (2.5, /3) ? = ? + ???? 0, 2 The region we are finding the area of is highlighted in green ? = ????? We can calculate the area of just the top part, and then double it (since the area is symmetrical) (2.5,- /3) 3 2
WB20b a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves 2 3 ? = ? + ???? 0 You need to imagine the top part as two separate sections Draw on the limits , and a line through the intersection, and you can see that this is two different areas ? = ????? 1) The area under the red curve with limits 0 and /3 2) The area under the blue curve with limits /3 and /2 3 2 We need to work both of these out and add them together! For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? ? =? ? = 0 3 ? =? ? =? 3 2
WB21c a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? ? =? 3 ? =? ? =? ? = 0 3 2 ? 1 2 For the red curve: ?2 ?? Sub in the values from above Also, remove the 1/2 since we will be doubling our answer anyway! ? ? 32 + ????2 ?? 0 Square the bracket ? 34 + 4???? + ???2? ?? Replace the cos2 term with an equivalent expression (using the equation for cos2 above) 0 ? 3 4 + 4???? +1 2???2? +1 2 ?? 0 Group like terms, and then we can integrate! ? 3 9 2+ 4???? +1 2???2? ?? 0
WB21d a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves For the red curve: ? = 2 + ???? For the blue curve: ? = 5???? ? =? 3 ? =? ? =? ? = 0 3 2 ? 3 9 2+ 4???? +1 For the red curve: 2???2? ?? Integrate each term, using standard patterns where needed 0 ? 3 9 2? + 4???? +1 4???2? Sub in the limits separately (as subbing in 0 will give 0 overall here, we can just ignore it!) 0 9 2 ? 3 ? 3 +1 2? 3 + 4??? 4??? Calculate each part (your calculator may give you a decimal answer if you type the whole sum in) 3? 2+ 2 3 + 3 8 Write with a common denominator 12? 8 +16 3 3 + 8 8 Group up 12? + 17 3 8
WB21e a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves For the red curve: For the blue curve: ? = 5???? ? =? 3 ???? =12? + 17 3 ? =? 8 2 ? 1 2 For the blue curve: ?2 ?? Sub in the values from above Also, remove the 1/2 since we will be doubling our answer anyway! ? ? 25????2 ?? ? 3 Square the bracket ? 225???2? ?? ? Replace the cos2 term with an equivalent expression (using the equation for cos 2 above) 3 ? 2 25 1 2???2? +1 ? ?? 2 We can move the 1/2 and the 25 outside to make the integration a little easier 3 ? 2 ???2? + 1 ?? 25 2 ? 3
WB21f a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves For the red curve: For the blue curve: ? = 5???? ? =? 3 ???? =12? + 17 3 ? =? 8 2 ? 2 ???2? + 1 ?? 25 2 ? For the blue curve: 3 Integrate each term, using standard patterns if needed ? 2 25 2 1 2???2? + ?? Sub in the limits (we do need to include both this time as neither will cancel a whole section out!) 3 25 2 1 2???? +? 1 2???2? 3+? 2 3 Calculate each part as an exact value 25 2 ? 2 4+? 3 3 Write with common denominators 25 2 6? 12 3 3 12+4? 12 Group up and multiply by 25/2 50? 75 3 24
WB21g a) On the same diagram, sketch the curves with equations: r = 2 + cos r = 5cos b) Find the polar coordinates of the intersection of these curves c) Find the exact value of the finite region bounded by the 2 curves For the red curve: For the blue curve: ???? =12? + 17 3 ???? =50? 75 3 8 24 Add these two areas together to get the total area! 12? + 17 3 8 +50? 75 3 24 Write with a common denominator 36? + 51 3 24 +50? 75 3 24 Add the numerators 86? 24 3 24 Divide all by 2 43? 12 3 12 These questions are often worth a lot of marks! Your calculate might not give you exact values for long sums, so you will need to be able to deal with the surds and fractions yourself!
KUS objectives BAT Find Areas bounded by parts of Polar curves BAT Find points of intersection of Polar curves self-assess One thing learned is One thing to improve is
Practice Ex 7D