Designing Elastomeric Vibration Isolators: Key Parameters and Configurations
Exploring the design aspects of elastomeric vibration isolators, including material selection, key design parameters, simple isolator configurations, spring rates, transmissibility, and shape factor calculations. Learn how engineered properties of elastomers can meet specific application requirements with ease of manufacturing and compact forms.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Introduction to Designing Elastomeric Vibration Isolators Christopher Hopkins OPTI 512 08 DEC 2009
Introduction Why elastomers? Key design parameters Loading Configuration Spring rates Design considerations Steps to designing a simple isolator
Elastomers An eastomer is any elastic polymer Silicone Rubber Butyl Rubber Fluorosilicone Rubber Material selection dependent on application Ulitimate Loading Sensitivity to Environment Internal Properties
Elastomeric Isolators Engineered properties can meet specific applications Modulus of elasticity Internal dampening Homogeneous nature allows for compact forms Easily manufactured Molded Formed in place
Key Isolator Design Parameters Configuration Loading Spring rate Shear, Bulk, and Young s modulus Geometry Ultimate strength Internal dampening Maximum displacement
Simple Isolator Configurations Planer Sandwich Form Laminate Cylindrical
Spring Rates Isolator spring rate sets system resonant frequency Ratio of resonant frequency to input frequency plus dampening control amount of isolation For an elastomer, spring rate is determined by Shape factor Loading: shear, compression, tension Material Properties: bulk, shear, and young s modulus
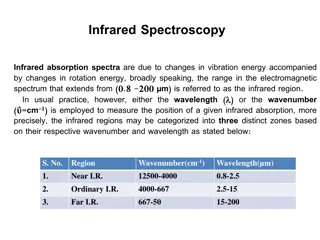
Transmissibility Transmissibility vs. Frequency Ratio 10 Transmissibility = 0.01 = 0.05 1 0 0.5 1 1.5 2 2.5 3 = 0.1 = 0.5 0.1 fr/f
Shape Factor Ratio of load area to bulge area Easy to calculate for simple shapes simply loaded Planer sandwich forms are simple Tube form bearings are more difficult, but can be approximated as a planer form
Shear Spring Rate Design isolator to attenuate in shear if possible Dependent on load area, thickness, and shear modulus Shear modulus is linear up to 75%-100% strain Shear modulus for large shape factors is also effected by high compressive loads When aspect ratio exceeds 0.25 a correction factor is added to account for bending
Compression Spring Rate Designed properly, compression can provide high stiffness Depends on load area, effective compression modulus, and thickness Effective compression modulus Linear up to 30% strain Can be tricky to compute
Tension Spring Rate Try to avoid having elastomeric isolators in tension Low modulus Can be damaged by relatively low loads Apply preload avoids this Easy to do for cylindrical isolators Must include correction to shape factor
Finding Modulus Many elastomers are listed with only with Durometer Shore hardness Ultimate strength (MPa or psi) Contacting manufacturer may be useful Perform tests Shear stress is 1/3 Young s modulus as poisson s ratio approaches 0.5 Use Gent s relation between Shore A hardness and Young s modulus (if you gotta have it now)
Effective Compression Modulus, Ec Dependent on shape factor, young s modulus and bulk modulus Also know as the apparent compressive modulus As Poisson s ratio approaches 0.5, Ecmay be separated into three zones depending on shape factor For large shape factors: Ec bulk modulus For small shape factors: Ec young s modulus Transisiton zone for intermediate shape factors
Computing Ec Gent provides a reference graph Hatheway found empirically that the transition zone is (Ec/E) (t/D)1.583=0.3660 Can calculate Ecor the simple case of a circular load area of diameter D and thickness t Find the break points First break point: (t/D)1.583= 0.366 (E/EB) Second break point: (t/D)1.583= 0.366
Compression Modulus vs. Shape Factor [Gent]
Stiffening vs. Thickness Ratio [Hatheway] Circular Cross Section, Eb=1.2 GPa, E=1.6 Mpa 1000 100 Stiffening Ratio Ec/E 10 1 0.0001 0.001 0.01 0.1 1 10 100 Thickness Ratio, t/D
Laminate Isolator Shear modulus is not effected by shape factor (if aspect ratio is <0.25) Effective compression modulus strongly influence by shape factor Possible to design an isolator that is very stiff in compression and compliant in shear
Cylindrical Isolator Shear Axial loading Torsion Compression Radial loading Shape factor calculation for compression
Design Considerations What is being Isolated? What are the inputs? Are there static loads? What are the environmental conditions? What is the allowable system response? What is the service life?
Example Design Process for a Simple Isolator Single excitation frequency Circular cross section, planar geometery All other components infinitely rigid Low dampening Attenuation provided in shear
Design Process Specifications Mass, input vibration, required attenuation, max displacement Use transmissibility to determine resonance frequency and spring rate Find isolator minimum area (A) Total number of isolators and max allowable stress Select modulus (G)
Design Process (cont) Knowing area (A), modulus (G), and spring rate (ks), calculate thickness (t) Calculate radius, verify aspect ratio < 0.25 to avoid bending effect Find static deflection Is static plus dynamic deflection < max allowable deflection? Find static shear strain Low strain reduces fatigue (<20%)
Conclusion Careful selection of parameters necessary to use methods presented. Can get complicated quick Low strains Low loads Try to stay clear of the transition zone between Young s and the bulk modulus For multiple input frequencies, need to consider if dampening ( ) is necessary May need to include considerations other than just isolation Stresses due to CTE mismatch
References P. M. Sheridan, F. O. James, and T. S. Miller, Design of components, in Engineering with Rubber (A. N. Gent, ed.), pp. 209{Munich:Hanser, 1992) A. E. Hatheway, Designing Elastomeric Mirror Mountings, Proc. of SPIE Vol. 6665 (2007) Daniel Vukobratovich and Suzanne M. Vukobratovich Introduction to Opto mechanical design A. N. Gent, On The Relation Between Indentation Hardness and Young s Modulus, IRI Trans. Vol. 34, pg.46-57 (1958)