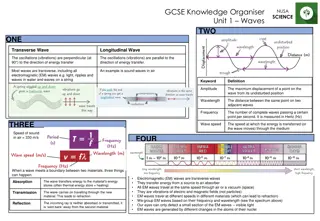
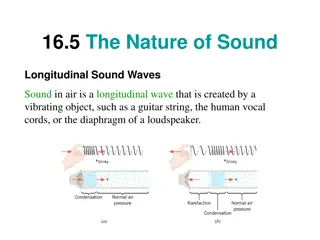
Understanding Interference and Beats in Waves
Explore the fascinating phenomena of interference and beats in waves, where overlapping waves interact to create patterns of constructive and destructive interference. Witness how sound waves can also produce beats when interfering in time, resulting in a slow envelope effect. Delve into the principles of superposition and discover the concept of beat frequency as the difference in frequency between two interfering waves.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Two overlapping waves interfere with each other 2
11-11 Interference; Principle of Superposition Constructive interference 3
11-11 Interference; Principle of Superposition Constructive interference Destructive interference 4
11-11 Interference; Principle of Superposition Constructive interference Destructive interference Somewhere in between 5
Two overlapping waves interfere with each other Constructive interference at C 6
Two overlapping waves interfere with each other Destructive interference at D 7
Interference of Sound Waves: Beats Waves can also interfere in time, causing a phenomenon called beats. Beats are the slow envelope around two waves that are relatively close in frequency. 8
Interference of Sound Waves: Beats Waves can also interfere in time, causing a phenomenon called beats. Beats are the slow envelope around two waves that are relatively close in frequency. Beat frequency = difference in frequency of the two waves 9
Interference of sound waves: Beats https://youtu.be/IQ1q8XvOW6g https://youtu.be/TrpQX5uKxQY 10
Interference of Sound Waves: Beats Waves can also interfere in time, causing a phenomenon called beats. Beats are the slow envelope around two waves that are relatively close in frequency. Beat frequency = difference in frequency of the two waves 11
12-52: Two piano strings are supposed to be vibrating at 220Hz , but a piano tuner hears three beats every 3.5s when they are played together. If one is known to be vibrating at 220Hz , what must be the frequency of the other? Is there only one answer? 3beats 3.5sec 3 f = = = Hz 0.85714 Hz The beat frequency is 3.5 The other string must vibrate at ( ) 220 0.85714 Hz 220.86 Hz 219.14 Hz or 12
The Doppler effect occurs when a source of sound moves with respect to an observer A stationary observer hears a firetruck s siren change in pitch as it drives by 14
They detect the same frequency Observer at rest Observer at rest Firetruck at rest 15
They detect the same frequency Observer at rest Observer at rest Firetruck at rest Firetruck moving Detects a lower frequency and longer wavelength Detects a higher frequency and shorter wavelength 16
The same thing happens if the truck is at rest and the observers move Firetruck at rest This person encounters fewer wavefronts per second when moving away from the truck than when standing still This person encounters more wavefronts per second when moving towards the truck than when standing still Therefore measures a lower frequency Therefore measures a higher frequency 17
The Doppler effect Suppose: sound v f is the frequency of the sound emitted by the source as measured when the source and observer are stationary ' f measured by the observer is the frequency and the sound source and/or the observer moves, and: is the speed of sound The frequencies are related as follows sound v v observer v v = ' f f sound source The upper signs apply if the source and observer move CLOSER TOGETHER The lower signs apply if the source and observer MOVE APART 18
iClicker Question Two people are moving closer together. Each will hear the other s voice A with a lower pitch B with a higher pitch C the same as when they were motionless D in a higher amplitude E in a lower amplitude 19
= 343m/s sound v Example 12-15: The siren of a police car at rest emits at a predominant frequency of 1600 Hz. What frequency will you hear if you are at rest and the police car moves at 25 m/s (a) towards you, and (b) away from you? (a) You and the police car are moving closer together: Use the upper signs = 0 observer v + sound v v observer v v f = 1600 Hz = ' f f = 25m/s source v sound source + 343 0 343 25 = = ' 1600 Hz 1726 Hz f ' 1726 Hz f = 20
= 343m/s sound v Example 12-15: The siren of a police car at rest emits at a predominant frequency of 1600 Hz. What frequency will you hear if you are at rest and the police car moves at 25 m/s (a) towards you, and (b) away from you? (b) You and the police car are moving apart: Use the lower signs = 0 observer v sound v v observer v v + f = 1600 Hz = ' f f = 25m/s source v sound source 343 0 343 25 + = = ' 1600 Hz 1491Hz f ' 1491Hz f = 21
= 343m/s sound v Example 12-15: The siren of a police car at rest emits at a predominant frequency of 1600 Hz. What frequency will you hear if you are at rest and the police car moves at 25 m/s (a) towards you, and (b) away from you? So, as the car approaches and moves past you, you hear the siren drop in pitch. Specifically, it goes from to 1726 Hz. 1491Hz 22
12.57: A bat at rest sends out ultrasonic sound waves at 46.5kHz and receives them returned from an object moving directly away from it at 31.5m/s . What is the received sound frequency? sound v v observer v v = ' f f sound source The upper signs apply if the source and observer move CLOSER TOGETHER The lower signs apply if the source and observer MOVE APART Assume the bat is at rest. The frequency received by the object is = sound v observer v + ' f f 0 sound v Bat Object 343m/sec 31.5m/sec 343m/sec = ' f f f = 46,500 Hz f = ' 42,229.6 Hz 23
12.57: A bat at rest sends out ultrasonic sound waves at 46.5kHz and receives them returned from an object moving directly away from it at 31.5m/s . What is the received sound frequency? Next, the sound bounces off the moving object and returns to the bat. So now we have a moving source and a stationary observer 24
12.57: A bat at rest sends out ultrasonic sound waves at 46.5kHz and receives them returned from an object moving directly away from it at 31.5m/s . What is the received sound frequency? sound v v observer v v = ' f f sound source The upper signs apply if the source and observer move CLOSER TOGETHER The lower signs apply if the source and observer MOVE APART Assume the bat is at rest. The frequency received by the bat is = 0 sound v '' ' f f + sound v source v Bat Object 343m/sec = '' ' f f 343m/sec+31.5m/sec f = ' 42,229.6Hz f = '' 38,677.6 Hz 38.7 kHz 25
So, the bat gets information about the object (e.g., an insect): How far away it is (time for the signal to return) Which way it is going and how fast (Doppler shift) 26
Measuring sound reflections is the basis of sonar (sound navigation ranging ) Locate things underwater Geology The method is also used in medical applications in combination with the Doppler effect The emitted and received signal can be mixed and the resulting beats can be measured Example: Monitoring the location, movements, and heartbeat of a fetus 27
The Doppler effect The source emits wavefronts at frequency f 1. f Wavefronts = T The time between emissions is Source = = sound v f Recall T = . T and therefore sound v 29
The Doppler effect Now suppose that the source moves toward the right with speed source v Source 30
The Doppler effect Now suppose that the source moves toward the right with speed source v In time T, it moves a distance = d source v T d source source ' This shortens the distance between the emitted wavefronts, so that Source = ' d source = ' source v T = ' source v sound v = T Recall that: sound v source v v = ' 1 sound 31
The Doppler effect source v v = ' 1 sound This is the wavelength that would be measured by a stationary observer d The observer would perceive a frequency given by source ' = ' ' sound v f sound v Observer Source = ' f ' 1 v v sound v = ' f 1 source sound f = ' f source v v 1 sound 32
The Doppler effect This is valid when the source moves TOWARDS the observer: sound v v f = ' f source v v d sound 1 source sound ' sound v Observer Source = ' f f sound v source v ' f f Notice: 33
The Doppler effect If the source moves AWAY from the observer, the same argument goes through but with a sign change (go back and check!!): d source sound v + = ' ' f f sound v source v Observer Source ' f f Notice: 34
The Doppler effect We can combine these results: d source ' sound v = ' f f sound v source v Observer Source Source moves toward observer: upper sign Source moves away from observer: lower sign 35
The Doppler effect What if the source is stationary, but the observer moves? Here, the observer moves towards the source. From the observer s perspective, the sound waves move at speed observer v sound v = + ' v sound v observer v Observer Source + ' sound v observer v f v = = ' f Thus the observer detects a frequency / sound v + sound v observer v sound v f = ' f f = = v f sound v 36
The Doppler effect What if the source is stationary, but the observer moves? Here, the observer moves TOWARDS the source. observer v + sound v observer v sound v = ' f f sound v Observer Source 37
The Doppler effect What if the source is stationary, but the observer moves? Here, the observer moves AWAY from the source. observer v sound v observer v sound v = ' f f sound v Observer Source 38
The Doppler effect All these results can be combined into this equation: sound v v observer v v = ' f f sound source The upper signs apply if the source and observer move CLOSER TOGETHER The lower signs apply if the source and observer MOVE APART 39