Understanding Standing Waves in Physics
Standing waves in physics are periodic waves that result from the interference of reflected and inverted waves, creating nodes and antinodes along a medium. These standing wave patterns can be observed in vibrating strings, such as guitar strings, where specific frequencies produce distinct harmonic frequencies. The concept of nodes, antinodes, and harmonic frequencies are essential in understanding the behavior of standing waves in various mediums.
Uploaded on Sep 26, 2024 | 0 Views
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
+ Standing Waves AP Physics 1
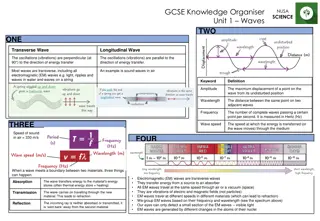
+Standing Waves Standing waves are periodic waves that are reflected and inverted so that they interfere with one another. The result of the interference is that specific points along the medium appear to be standing still while other points vibrated back and forth. NODES: locations of total destructive interference ANTINODES: locations of constructive interference .
+Pitch Pitch is our brain s interpretation of frequency. 440 Hz is typically concert pitch and is the A above middle C.
+Harmonics Such patterns are only created within the medium at specific frequencies of vibration. These frequencies are known as harmonic frequencies or merely harmonics. At any frequency other than a harmonic frequency, the interference of reflected and incident waves results in a disturbance of the medium that is irregular and non-repeating n is called the harmonic number n = 1 is the fundamental frequency n= 2 is the 2ndharmonic n = 3 is the 3rdharmonic, etc.
+Standing Waves for Vibrating Strings This is just one possible example. There are a variety of patterns by which the guitar string could naturally vibrate.
+Standing Waves for a Vibrating String Each pattern is associated with one of the natural frequencies of the guitar strings.. Each standing wave pattern is referred to as a harmonic of the instrument (in this case, the guitar string). The three diagrams at the right represent the standing wave patterns for the first, second, and third harmonics of a guitar string.
+ For guitar strings, each pattern is characterized by some basic traits: There is an alternating pattern of nodes and antinodes. There are either a half-number or a whole number of waves within the pattern established on the string. Nodal positions (points of no displacement) are established at the ends of the string where the string is clamped down in a fixed position. One pattern is related to the next pattern by the addition (or subtraction) of one or more nodes (and antinodes).
+Nodes at each end of string First, consider a guitar string vibrating at its natural frequency or harmonic frequency. Because the ends of the string are attached and fixed in place to the guitar's structure (the bridge at one end and the frets at the other), the ends of the string are unable to move. Subsequently, these ends become nodes - points of no displacement. In between these two nodes at the end of the string, there must be at least one antinode.
+Vibrating String: Fundamental Frequency The most fundamental harmonic for a guitar string is the harmonic associated with a standing wave having only one antinode positioned between the two nodes on the end of the string. This would be the harmonic with the longest wavelength and the lowest frequency. The lowest frequency produced by any particular instrument is known as the fundamental frequency. The fundamental frequency is also called the first harmonic of the instrument.
+Vibrating String: 2ndHarmonic The second harmonic of a guitar string is produced by adding one more node between the ends of the guitar string. And of course, if a node is added to the pattern, then an antinode must be added as well in order to maintain an alternating pattern of nodes and antinodes. In order to create a regular and repeating pattern, that node must be located midway between the ends of the guitar string . This additional node gives the second harmonic a total of three nodes and two antinodes. The standing wave pattern for the second harmonic is shown at the right. A careful investigation of the pattern reveals that there is exactly one full wave within the length of the guitar string. For this reason, the length of the string is equal to the length of the wave.
+Vibrating String: 3rdHarmonic The third harmonic of a guitar string is produced by adding two nodes between the ends of the guitar string. And of course, if two nodes are added to the pattern, then two antinodes must be added as well in order to maintain an alternating pattern of nodes and antinodes. In order to create a regular and repeating pattern for this harmonic, the two additional nodes must be evenly spaced between the ends of the guitar string. This places them at the one-third mark and the two-thirds mark along the string. These additional nodes give the third harmonic a total of four nodes and three antinodes. The standing wave pattern for the third harmonic is shown at the right. A careful investigation of the pattern reveals that there is more than one full wave within the length of the guitar string. In fact, there are three-halves of a wave within the length of the guitar string. For this reason, the length of the string is equal to three-halves the length of the wave.
+Vibrating Strings: Pattern Harmonic # # Waves in String # Nodes # Antinodes Wavelength- Length Relationship 1 2 3 4 5
+Vibrating String Example Problem Consider an 80-cm long guitar string that has a fundamental frequency (1st harmonic) of 400 Hz. What is the wavelength of the wave pattern produced? What is the speed of this standing wave? Find the wavelength, speed and frequency for the 2ndand 3rd harmonics.
+Vibrating String: Frequencies the individual frequencies in the set of natural frequencies produced by a guitar string are related to each other by whole number ratios. The frequency of the second harmonic is two times the frequency of the first harmonic. The frequency of the third harmonic is three times the frequency of the first harmonic. The frequency of the nth harmonic (where n represents the harmonic # of any of the harmonics) is n times the frequency of the first harmonic. In equation form, this can be written as fn= n f1
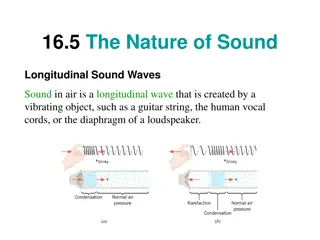
+Open-End Air Columns Many musical instruments consist of an air column enclosed inside of a hollow metal tube. Though the metal tube may be more than a meter in length, it is often curved upon itself one or more times in order to conserve space. If the end of the tube is uncovered such that the air at the end of the tube can freely vibrate when the sound wave reaches it, then the end is referred to as an open end. If both ends of the tube are uncovered or open, the musical instrument is said to contain an open-end air column. A variety of instruments operate on the basis of open-end air columns; examples include the flute and the recorder. Even some organ pipes serve as open-end air columns.
+Standing Wave Patterns in Air Columns In the case of stringed instruments (discussed earlier), standing wave patterns were drawn to depict the amount of movement of the string at various locations along its length. Such patterns show nodes - points of no displacement or movement - at the two fixed ends of the string. In the case of air columns, a closed end in a column of air is analogous to the fixed end on a vibrating string. That is, at the closed end of an air column, air is not free to undergo movement and thus is forced into assuming the nodal positions of the standing wave pattern. Conversely, air is free to undergo its back-and-forth longitudinal motion at the open end of an air column; and as such, the standing wave patterns will depict antinodes at the open ends of air columns. So the basis for drawing the standing wave patterns for air columns is that vibrational antinodes will be present at any open end and vibrational nodes will be present at any closed end.
+Open-End Air Column: 1stharmonic the pattern for the fundamental frequency (the lowest frequency and longest wavelength pattern) will have antinodes at the two open ends and a single node in between. The distance between antinodes on a standing wave pattern is equivalent to one-half of a wavelength. A careful analysis of the diagram above shows that adjacent antinodes are positioned at the two ends of the air column. Thus, the length of the air column is equal to one- half of the wavelength for the first harmonic.
+Open-End Air Column: 2ndharmonic total of three antinodes and two nodes. there is one full wave in the length of the air column. One full wave is twice the number of waves that were present in the first harmonic. For this reason, the frequency of the second harmonic is two times the frequency of the first harmonic.
+Open-End Air Column: 3rd harmonic a total of four antinodes and three nodes. there are one and one-half waves present in the length of the air column. One and one- half waves is three times the number of waves that were present in the first harmonic. For this reason, the frequency of the third harmonic is three times the frequency of the first harmonic.
+Open-End Air Columns: Pattern Harmonic # # Waves in String # Nodes # Antinodes Wavelength- Length Relationship 1 2 3 4 5
+Closed-End Air Columns An instrument consisting of a closed-end column typically contains a metal tube in which one of the ends is covered and not open to the surrounding air. Some pipe organs and the air column within the bottle of a soda-bottle orchestra are examples of closed-end instruments. Some instruments that operate as open-end air columns can be transformed into closed-end air columns by covering the end opposite the mouthpiece with a mute. As we will see the presence of the closed end on such an air column will affect the actual frequencies that the instrument can produce.
+Standing Wave Patterns in Air Columns (again ) In the case of stringed instruments (discussed earlier), standing wave patterns were drawn to depict the amount of movement of the string at various locations along its length. Such patterns show nodes - points of no displacement or movement - at the two fixed ends of the string. In the case of air columns, a closed end in a column of air is analogous to the fixed end on a vibrating string. That is, at the closed end of an air column, air is not free to undergo movement and thus is forced into assuming the nodal positions of the standing wave pattern. Conversely, air is free to undergo its back-and-forth longitudinal motion at the open end of an air column; and as such, the standing wave patterns will depict antinodes at the open ends of air columns. So the basis for drawing the standing wave patterns for air columns is that vibrational antinodes will be present at any open end and vibrational nodes will be present at any closed end.
+Closed-End Air Column: 1stharmonic the pattern for the fundamental frequency (the lowest frequency and longest wavelength pattern) will have a node at the closed end and an antinode at the open end. The distance between an antinode and a node must be equivalent to one-fourth of a wavelength. A careful analysis of the diagram above shows that a node and an adjacent antinode are positioned at the two ends of the air column. Thus, the length of the air column is equal to one- fourth of the wavelength for the first harmonic.
+Closed-End Air Column: 3rd harmonic . Just as for all the instruments, the next harmonic for a closed-end air column is the harmonic that has one more node. And just as for all the instruments, the addition of an extra node also means that an extra antinode must also be added to the pattern. This would result in a total of two vibrational antinodes and one vibrational node Observe in the pattern that there is three-fourths of a full wave in the length of the air column. That is three times the number of waves in the first harmonic. Since, the frequency of this harmonic is three times the frequency of the first harmonic, this is called the third harmonic.
+What happened to the 2nd harmonic? what happened to the second harmonic? Unlike the other instrument types, there is no second harmonic for a closed-end air column. The next frequency above the fundamental frequency is the third harmonic (three times the frequency of the fundamental). In fact, a closed-end instrument does not possess any even-numbered harmonics. Only odd-numbered harmonics are produced, where the frequency of each harmonic is some odd-numbered multiple of the frequency of the first harmonic.
+Closed-End Air Column: 5thharmonic the standing wave pattern for the fifth harmonic of a closed- end air column is produced by adding another node to the pattern. This would result in a total of three anti-nodes and three nodes. Observe in the pattern that there are one and one-fourth waves present in the length of the air column. That is five times the number of waves in the first harmonic. For this reason, the frequency of the fifth harmonic is five times the frequency of the first harmonic.
+Closed-End Air Columns: Pattern Harmonic # # Waves in String # Nodes # Antinodes Wavelength- Length Relationship 1 2 3 4 5