Efficient Solver Techniques in CFD Simulations
This resource provides insights into the segregated solver approach in computational fluid dynamics (CFD) simulations, specifically focusing on the sweeping direction and its impact on computational efficiency and convergence rates. It discusses the benefits of employing the XY plane for 2D cases to reduce CPU time and accelerate convergence. The importance of aligning the Z direction with the main flow direction in 3D simulations is also highlighted. Additionally, it emphasizes the significance of selecting appropriate boundary conditions and initial data for achieving a converged numerical solution in CFD simulations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
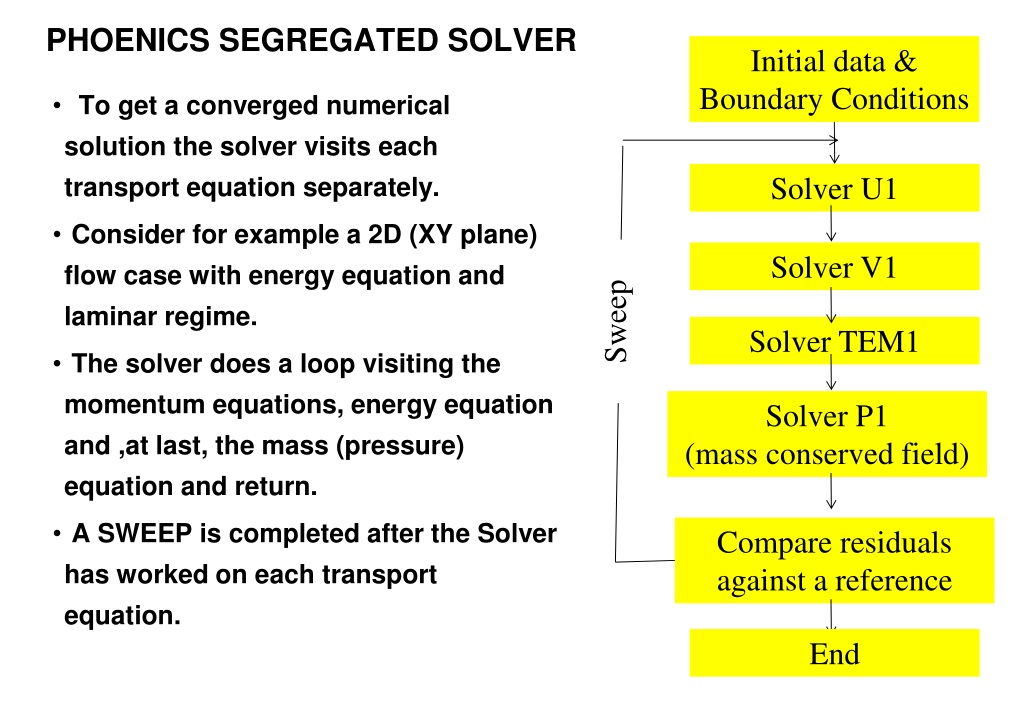
PHOENICS SEGREGATED SOLVER Initial data & Boundary Conditions To get a converged numerical solution the solver visits each transport equation separately. Solver U1 Consider for example a 2D (XY plane) flow case with energy equation and laminar regime. Solver V1 Sweep Solver TEM1 The solver does a loop visiting the momentum equations, energy equation and ,at last, the mass (pressure) equation and return. Solver P1 (mass conserved field) A SWEEP is completed after the Solver has worked on each transport equation. Compare residuals against a reference End
Solver Sweeping Direction(1) Each transport equation is visited by the solver individually; The computational domain is not tackled at once by the solver. It slices the domain in slabs (XY plane) along the Z direction. The sweep starts from low Z to high Z, or IZ = 1 to IZ = last. The solver sweeping direction has a direct influence on the computer time and some times on the convergency rate. For 3D simulation align the Z direction along the main flow direction. This practice propagates faster the upstream information to the downstream direction
Solver sweeping direction: two dimensional cases (2) For 2D cases employ the XY plane; the solution is faster because the solver has only one slab to sweep. Furthermore, it solves at once the whole slab . Y Z 4 sweeps Z X X Y Workshop #1: compare the CPU time for the cylinder in cross flow using the XY and YZ planes. One can download the q1XY and q1YZ.
Both simulations have the same inlet values, fluid properties, grid size and reference residuals. COMENTS Case 2D The XY plane requires 5200 sweeps to fall below the threshold level and stop simulation. The YZ plane doesn t reach threshold even after the 8000 sweeps XY CPU time = 22sec (5200 sweeps) YZ CPU time = 222s (8000 sweeps); it is a 10 times faster if one uses the XY plane. One concludes that using XY plane reduces the CPU time and also speeds convergence! Cilindrical-Polar, 3D The Z direction is the Phoenics natural choice to be the axis parallel to the coordinate system axial direction. Cases and BFC For 3D it is highly recommended to choose the main flow direction coincident with the Z axis. For 3D BFC it is mandatory that the main flow direction be coincident with the Z axis. BFC two dimensional cases one must choose the XY plane only.
Initial data & Boundary Conditions The next sections introduces Phoenics tools to access and control convergence. Solver U1 Solver V1 Sweep Solver TEM1 Solver P1 The type and the use of these new tools are closely related to the solver s segregated structure. (mass conserved field) Compare residuals against a reference End
Getting a Numerical Solution is a Difficult Task 1. Grid independent - if you increase the number of nodes the solution does not change significantly. Convergence the solution achieves a constant value, it does not oscillates neither changes with further interactions; Negligible Residuals if the mass, momentum, energy (and other variables) residuals are negligible one can say the numerical solution satisfies GLOBALLY the conservation equations. 2. 3. Usually if you get convergence but not get negligible residuals your solution is converged to a non-physical (wrong) solution! A number of devices are provided in PHOENICS to monitor and control the convergence of the solution. They are fully described at Convergence Monitoring link and are briefly presented now.
THE RESIDUALS & CONVERGENCE MONITORING The residuals are the quantities used in PHOENICS to monitor the convergence procedure. These are the imbalances in the FVE, defined as: During the computation, the residuals are printed by Earth to the VDU, or are displayed graphically. The frequency of display update is controlled by the PIL variable TSTSWP, which is set in the menu from the Monitoring controls/Residuals display frequency panel. The default value of 1 prints to the screen, which is suitable for batch operation. A setting TSTSWP = -1 activates the graphical display.
THE SPOT VALUE (GROUP 22) In addition to the display of residuals to the screen, the values of chosen variables for a single cell can also be displayed. A monitoring location (or cell) is selected in the Q1 file, or from the menu by setting the variables IXMON, IYMON, IZMON to the values of IX, IY and IZ of the cell to be monitored. The monotoring spot can be set on VR/Output box.
MONITORING SPOT VALUES AND RESIDUALS ON SCREEN SPOT VALUES RESIDUALS
NORMALIZING THE RESIDUALS The quantities printed out are, in fact: where the sum is extended to the current slab (in PARABolic cases) or to the whole field (in elliptic cases). When the sum of errors divided by RESREF falls below 1.0, solution for that variable stops. When this happens for all variables, sweeping stops. EARTH can calculate values for RESREF, based on the net sum of fluxes for a variable, if the PIL variable SELREF=T. The supplementary variable RESFAC acts as a tolerance - a setting of 0.01 means that sweeping stops when the errors are 1% of the reference fluxes.
RESREF , RESFAC & SELREF (GROUP 15) RESREF, the reference-residual for a solved-for variable It is evaluated by RESREF = RESFAC*(Typical flow rate of the variable) The "typical flow rate" is the sum of the absolute values, for all cell volumes and cell faces, of the convection fluxes, diffusion fluxes, sources and transient terms. If SELREF = T Earth evaluates internally RESREF If SELREF = F RESREF is user set. Users should be aware that the employment of SELREF=T, with a value of RESFAC which is the same for all variables, is a convenient but crude method of controlling the cut-off point of the solution procedure. To set SELREF = F, and set the individual RESREFs for themselves may be safer, when obtaining a well-converged solution is especially important.
VR SETTINGS: SWEEPS RESFAC SELREF
1.1 WORKSHOP#2: ANALYSING RESIDUALS
WORKSHOP NOTES CONVERGENCE AND CONTROL #2 Load core library case 240. This case deals with the entry flow in a 2-D parallel walls channel. Now make the changes: y size from 1 m to 0.5 m; NY = 10 and NZ = 15; set the domain to material 67 (water); LSWEEP = 200 ; Turn off the Energy Equation and finally make WIN = 0.01 m/s instead of 5 m/s
WORKSHOP NOTES CONVERGENCE AND CONTROL #2 Run EARTH. Inspect the RESULT file to check the assigned RESREF values. variable resref (res sum)/resref (res sum) P1 5.018E-04 4.528E-04 2.272E-07 V1 1.213E-08 8.297E+03 1.006E-04 W1 4.693E-06 7.178E+01 3.369E-04 Can you give a physical meaning to them? DOWNLOAD WKSH Q1
WORKSHOP #2 NOTE (1) Whole-field residuals before solution with RESREF values determined by EARTH & RESFAC = 1.00E-03 & TIME/(VARIABLES*CELLS*TSTEPS*SWEEPS*ITS = 9E-05 sec. variable resref (res sum)/resref (res sum) P1 5.018E-04 4.528E-04 2.272E-07 V1 1.213E-08 8.297E+03 1.006E-04 W1 4.693E-06 7.178E+01 3.369E-04 1- the 4thcolumn means that the sum of residuals of pressure, for example, is nearly 2.3E-7 (kg/s). Similarly to the other variables. 2- The meaning of the 2ndcolumn is a reference flux. Thus for pressure (mass conservation) it is 5.0E-04 kg/s, and for V1 and W1 it is the mass flux times a reference velocity, 1.0E-08 kgm/s2(N) and 4.7E-06 kgm/s2(N). 3- How big or small these fluxes are? One have to compare against some characteristic value of the problem. 4- Inlet mass flux = RHO1*WIN*H = 5 kg/s; W1 momentum flux = 5E-02 N, V1 momentum flux (very small, boundary layer) 5- The mass imbalance (sum of residuals) is 2.3E-07 kg/s or 5-10% of the mass inlet! If the run had stopped at (res sum)/resref = 1, then the global mass imbalance would correspond to 0.01% of the mass inlet. The same reasoning applied to W1 and V1 one sees that the residuals are far from satisfy the convergence criterion.
WORKSHOP NOTES CONVERGENCE AND CONTROL #2 Open q1 file and edit the following lines: SELREF=F RESREF(V1) = 5.0E-06 kg.m/s2 [N], RESREF(W1) = 5.0E-06 kg.m/s2[N] and RESREF(P1) = 5.0E-04 kg/s. These changes can not be made using VR, you have to edit q1 file directly. (there is a hint on editing in note 2). Compare with the actual run performance with the one from last case. variable resref (res sum)/resref (res sum) P1 5.018E-04 4.528E-04 2.272E-07 V1 1.213E-08 8.297E+03 1.006E-04 W1 4.693E-06 7.178E+01 3.369E-04
WORKSHOP #2 NOTE (2) Edit GROUP 15 in q1 file using the notepad: ************************************************************ Group 15. Terminate Sweeps LSWEEP = 200 RESREF(P1 ) = 5.000000E-04 ;RESREF(V1 ) = 5.000000E-06 RESREF(W1 ) = 5.000000E-06; SELREF = F Save and close notepad DO NOT FORGET: RELOAD WORKING FILE Whole-field residuals with resref values set by the user variable resref (res sum)/resref (res sum) P1 5.000E-04 5.016E-04 2.508E-07 V1 5.000E-06 3.409E+01 1.704E-04 W1 5.000E-06 1.758E+02 8.788E-04 The criteria to stop V1 was eased. As a consequence the solution for W1 got worse probably because the V1 residuals were too coarse. One may use the SELREF =T or decide by himself the reference residuals, this is the most important convergence criterion.
2. PROMOTING & ACHIEVING CONVERGENCE
What if your numerical solution blows up? What if the residuals of your numerical solution does not fall bellow a specified threshold value ? Phoenics has several commands to control the numerical convergency rate which are represented by : 1. Control of the number of iteration per variable and the termination criteria; 2. The prescription for a variable of the range of values it can take; 3. The use of relaxation;
ASSESING CONVERGENCE There are several guidelines to follow and observe when trying to assess whether a run has converged or not. These are: Have the values at the monitor point stopped changing? Have the residuals reached the cut-off point, or reduced by several orders of magnitude in any case? Do the sums of sources printed in the RESULT file balance? Are plots taken from PHI files dumped, say 200, sweeps apart essentially identical? If the answers the first three questions are all yes, then the run has almost definitely converged. The fourth test can be used just to make sure, if you are not convinced. Intermediate PHI files can be dumped from the EARTH interrupt, or by appropriate settings in the Q1.
2.1 - MATRIX SOLVER CONTROLER: NUMBER OF ITERATIONS PER VARIABLE AND TERMINATION CRITERIA
MATRIX SOLVER CONTROLER: NUMBER OF ITERATIONS PER VARIABLE AND TERMINATION CRITERIA Each variable is visited by the solver LITER times before the solver moves to the next one. LITER(phi)....maximum number of iterations which are to be performed by the linear-equation solver for the variable phi, when such a solver is being employed for it. Initial data & Boundary Conditions Solver U1 LITER ENDIT Solver V1 Sweep Solver TEM1 ENDIT----- Real array; default= 1.E-3; Satellite Help - When greater than zero, ENDIT influences the termination of iterations in the built-in linear- equation solver by requiring that, before termination can occur, the average change of value is less than ENDIT times the average change at the first iteration (unless LITER iterations have been performed). Solver P1 (mass conserved field) Compare residuals against a reference End
MATRIX SOLVER CONTROLER: NUMBER OF ITERATIONS PER VARIABLE AND TERMINATION CRITERIA The convergence process is interactive. The solver visits one variable at a time. Therefore is not necessary to get a error free solution at the beginning of the process since the other variables are not fully converged. This means: LITER large will demand large machine time to get a solution; LITER small probably will not guarantee a converged solution since the intermediate solutions are not well resolved; ENDIT small will use all the sweeps specified in the LITER; ENDIT big will cause the solver leave the variable without a reasonable solution;
2.2 - MATRIX SOLVER CONTROLER: LIMITING THE RANGE OF VALUES
VARIABLE CONTROL LIMITING THE RANGE OF VALUES (GROUP 18) A variable can be prevented from overshooting, during the iteration procedure, the range of physically-realistic values by using the PIL commands VARMIN (variable) and VARMAX(variable) to prescribe that range. Then, PHOENICS will use those values as lower and upper bounds for the field of the variable. It is usefull for solved variables such as Turbulent Kinetic Energy and Dissipation which have always positive values! The use of VARMIN and VARMAX is not limited to solved for variables; it can also be used with any STOREd one. For example, after STOREing the density or the turbulent viscosity, VARMIN can be used to avoid negative values during the iteration process. Note, however, that if any values are left at VARMIN or VARMAX in the converged flow-field, the flow is NOT converged. The limits must be eased, and the run continued.
2.3 - MATRIX SOLVER CONTROLER: RELAXATION (very important)
Relaxation is a commonly-used device that promotes convergence by "slowing down" ("relaxing") the (sometimes excessive) changes made to the values of the variable during the solution procedure. RELAXATION Initial data & Boundary Conditions Relaxation involves, therefore, changing the values obtained from the solution algorithm, so that they are closer to the pre-existing ones. Solver U1 Solver V1 Sweep How the values are changed gives rise to two kinds of relaxation: Solver TEM1 1.Linear relaxation Solver P1 2.False time-step (or inertial) relaxation (mass conserved field) relax Both options are available in PHOENICS (PIL group 17 or the menu), and their activation is discussed next. Compare residuals against a reference However, before proceeding with the discussion, it must be stressed that relaxation does NOT change the converged solution, but only the RATE at which the solution is achieved. End
1. Linear Relaxation When linear relaxation is applied to a variable f, the new value new for the variable at each cell is taken as: new = (1 - ) old + * where: old is the current in-store value, resulting from the previous iteration; and * is the value which results from the current iteration; and is the relaxation factor. Obviously: if = 0, then new = old (i.e., no change at all) if = 1, then new = * (i.e., no relaxation at all) The PHOENICS command to activate linear relaxation for a variable is: RELAX( , LINRLX , )
2. False-Time-Step Relaxation False-time-step relaxation results from adding to the RHS of the FVE an extra term: where: P is the cell-value of to be computed, is the cell-value of resulting from the previous iteration, V is the cell volume and dtf is a user-set false-time-step Large values of dtf, the added extra term is negligible, and the solution of the equation is the same as the unrelaxed one. Small values of dtf, the solution is change at all). (i.e., no The name false-time-step arouse because the extra added term has the same form as the one resulting from the transient term even if the problem is steady state.
False-Time-Step Relaxation - cont dtf can be set finding a characteristic time scale of the phenomena: Convective time scale: dtf ~ L/U Difusive time scale: dtf ~ L2 / The PHOENICS command to activate linear relaxation for a variable is: RELAX ( f , FALSDT , time-step ) where time-step = dtf.
Expert Systems to Achieve Fast Convergency EXPERT: A set of 'auto-pilot' devices have been introduced which make 'in- flight' adjustments to the numerical parameters (such as relaxation factors) in order to speed up the convergence of the solution procedure. Look after the Encyclopedia to activate Expert. SARAH (Self-Adjusting Relaxation AlgoritHm): Much in the same way that EARTH can calculate normalising factors for residuals when SELREF=T based on sums of fluxes, it can also calculate average time- scales for each variable. Look after the Encyclopedia to activate Expert. CONWIZ (Convergency Wizard): is a feature of PHOENICS 3.6 which is designed to ensure that PHOENICS solutions will converge, whenever the input data are sufficient and self-consistent. See entry at Encyclopedia
WORKSHOP #3 CONVERGENCE AND CONTROL Reload 2D rectangular channel flow . Set the Auto Converg Control to OFF Set FALSDT to W1 and V1 to 1 Set SWEEPS to 600 -------------------------------------------- Comments: The residuals are lower than previous case. Return to the Auto-Convergence mode. Set the reference velocity and scale to: 0.01m/s & 0.5m and run again the case. DOWNLOAD WKSH Q1
WORKSHOP #4 CONVERGENCE AND CONTROL Load core library case 252. This case deals with natural convection in an annular cavity. At the OUTPUT box activate the graphics monitor convergence; TSTSWP = -1 At the NUMERICS box change the sweeps from 150 to 600; LSWEEP = 600 After you completed these changes run EARTH. The solution must converge within the 300 sweeps.
WORKSHOP NOTES CONVERGENCE AND CONTROL #1 THE DANGER OF OVER-RELAXATION Now change the relaxation settings of U1, V1 and H1 to FALSDT = 1.0E+04 and watch the monitor plots (see NOTE 2 for help if you need). In many cases even moderate amounts of relaxation can speed up convergence dramatically. In other cases, it is the only difference between convergence and divergence!
WORKSHOP NOTES CONVERGENCE AND CONTROL THE DANGERS OF UNDER RELAXATION Run the case again. This time put in extremely heavy relaxation (FALSDT = 1.0E-8) and see how the solution behaves. Can you explain this behavior? See note 3 if you need help. Answer: you have introduced so much relaxation that the momentum equations can no longer change themselves. Pressure correction is still active, and will change the velocities so as to satisfy continuity. The P1 residual will therefore be very low, but the velocity residuals will be high and stuck. Setting FALSDT to 1.0E-8 is an extremely heavy under relaxation which will probably freeze the variables.
ADDTIONAL REMARKS When divergence occurs it is necessary to establish the cause. It may be found in the strength of the linkages between two or more sets of equations, which are being solved. in turn rather than simultaneously. For example in Free Convection heat transfer is a strongly coupled with the energy and the velocity field. They influence each other and may be a common source of divergence. Whether it is or not THE source in a particular case can be established by freezing the temperature field before the divergence has progressed too far and seeing if the divergence persists. If it DOES NOT, the velocity-temperature link can be regarded as the source of divergence; otherwise the cause must be sought in some other linkage.
PLAYING WITH RELAXATION Explore how different choices of relaxation factors affect the required number of SWEEPS to get convergence. Fill in the Table below P1 -1 V1 1 U1 1 AUTO 2 200 0.1 H1 1 SWEEPS AUTO -1 -1 -1 AUTO 2 200 0.1 AUTO 10 100 0.1
CHANGING THE RESFAC Objective: evaluate the number of sweeps necessary to get CONVERGENCY by changing the RESFAC Fill in the Table below 400 RESFAC 1% 0.1% 0.01% 0.001% N. SWEEPS 300 SWEEPS 200 100 0 0.001 0.01 RESFAC (%) 0.1 1
PLAYING WITH LITER Explore how different choices of LITER affect the required number of SWEEPS and the CPU time to get convergence. Use RESFAC = 0.1% and ENDIT = 1E-3 Fill in the Table below P1 20 30 10 2 V1 10 20 5 1 U1 10 20 5 1 H1 20 30 10 2 SWEEPS CPU Time/Var
LAST REMARK ON CONVERGENCE AND NEGLIGIBLE RESIDUALS After applying the available tools to access convergence and negligible residuals with no success consider REVIEW YOUR GRID. Try to work with coarse grids at start and then progressively refine them. Be alert to flow regions with steep gradients, typical of Boundary Layer. Try to refine the grid on these regions to capture the steep gradients. Avoid working with grids exhibiting large aspect ratios, i.e. larger than 20:1
PLAYING WITH RELAXATION Explore how different choices of relaxation factors affect the required number of SWEEPS to get convergence. Fill in the Table below P1 -1 V1 1 U1 1 AUTO 2 200 0.1 H1 1 SWEEPS 240 569 54 no conv too slow AUTO -1 -1 -1 AUTO 2 200 0.1 AUTO 10 100 0.1
CHANGING THE RESFAC Objective: evaluate the number of sweeps necessary to get CONVERGENCY by changing the RESFAC Fill in the Table below 400 RESFAC 1% 0.1% 0.01% 0.001% N. SWEEPS 300 SWEEPS 200 100 0 0.001 0.01 RESFAC (%) 0.1 1
PLAYING WITH LITER Explore how different choices of LITER affect the required number of SWEEPS and the CPU time to get convergence. Use RESFAC = 0.1% and ENDIT = 1E-3 Fill in the Table below P1 20 30 10 2 V1 10 20 5 1 U1 10 20 5 1 H1 20 30 10 2 SWEEPS 240 238 245 260 CPU 2 2 2 5 Time/Var 2.08x10-5 2.10x10-5 2.04x10-5 4.80x10-5