Understanding Maxwell Equations in Thermodynamics
In thermodynamics, Maxwell equations are derived using Euler's reciprocity relation. They involve characteristic functions such as internal energy, free energy, enthalpy, and Gibbs free energy, along with parameters like temperature, entropy, pressure, and volume. These equations form the foundation of classical electromagnetism, optics, and electric circuits. Maxwell's equations describe how electric charges and currents create electric and magnetic fields, showing the interplay between them. The elegance and mathematical sophistication of Maxwell's equations make them essential in understanding electricity and magnetism.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
MEDICAL ENGINEERING DEPT SECOND YEAR THERMODYNAMICS INTRODUCTION PART ONE
Maxwell Equations (Thermodynamics) In thermodynamics, the Maxwell equations are a set of equations derived by application of Euler's reciprocity relation to the thermodynamic characteristic functions. The Maxwell relations, first derived by James Clerk Maxwell, are the following expressions between partial differential quotients: 2
Maxwell Equations (Continue) The characteristic functions are: U (internal energy), A (Helmholtz free energy), H (enthalpy), and G (Gibbs free energy). The thermodynamic parameters are: T (temperature), S (entropy), P (pressure), and V (volume) As an example of a derivation, consider Euler's reciprocity relation reads: 3
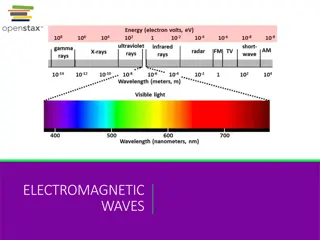
Maxwell Equations (Continue) Maxwell's differential equations that, together with the Lorentz force law, form the foundation of classical electromagnetism, classical optics, and electric circuits. ... Maxwell first used the equations to propose that light is an electromagnetic phenomenon. equations are a set of coupled partial They describe how electric charges and electric currents create electric and magnetic fields. They describe how an electric field can generate a magnetic field, and vice versa. ... The second allows one to calculate the magnetic field. 5
Maxwell Equations (Continue) According electromagnetic field is generated by a change in magnetic flux, the polarity of the induced electromagnetic field produces an induced current whose magnetic field opposes the initial changing magnetic field which produced it. to law, when an Lenz's 6
Maxwell's Equations Maxwell's equations represent one of the most elegant and concise ways to state the fundamentals of electricity and magnetism. From them one can develop most of the working relationships in the field. Because of their concise statement, they embody a high level of mathematical sophistication and are therefore not generally introduced in an introductory treatment of the subject, except perhaps as summary relationships. These basic equations of electricity and magnetism can be used as a starting point for advanced courses, but are usually first encountered as unifying equations after the study of electrical and magnetic phenomena 7
Maxwell Equations (Continue) Symbols Used E = Electric field = charge density i = electric current B = Magnetic field 0= permittivity J = current density D = Electric displacement 0= permeability c = speed of light H = Magnetic field strength M = Magnetization P = Polarization 8
Maxwell's Equations (Continue..) Integral form in the absence of magnetic or polarizable media: I. Gauss' law for electricity II. Gauss' law for magnetism 9
Maxwell's Equations (Continue..) III. Faraday's law of induction IV.Ampere's law 10
Maxwell's Equations (Continue..) I. Gauss' law for electricity II. Gauss' law for magnetism III. Faraday's law of induction 11
Maxwell's Equations (Continue..) IV.Ampere's law here represent the vector operations divergence and curl, respectively 12
Maxwell's Equations (Continue..) Differential form with magnetic and/or polarizable media I. Gauss' law for electricity II. Gauss' law for magnetism 13
Maxwell's Equations (Continue..) III. Faraday's law of induction IV.Ampere's law 14

 undefined
undefined