Exploring Multiplication Concepts in Key Stage 1
Explore various aspects of teaching multiplication in Key Stage 1, including multiple representations, developing fluency, conceptual understanding, integrating fluency with understanding, and practical applications like grid multiplication and arrays. See how educators support children in mastering multiplication through a comprehensive approach.
- Multiplication Concepts
- Key Stage 1
- Teaching Strategies
- Educational Resources
- Mathematics Instruction
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Areas addressed Multiple Representations Representing multiplication in Key Stage 1 The commutative law for multiplication Grid multiplication as an interim step Moving from grid to a column method 2
Multiple Representations Representing multiplication in Key Stage 1
Developing fluency The children have been counting in steps of 2, 5 and 10 and practising multiplication facts. How is this supporting children s fluency in multiplication? 4
Conceptual understanding The teacher stops and shows different representations of multiplication facts on the whiteboard and the children are required to match symbols to pictures. How might this support children s conceptual understanding of multiplication? 5
What do you notice? Sam says: What we are trying to focus on is not children just learning table facts by heart or by rote and not understanding what it means . How does Sam attempt to integrate fluency with understanding? 6
Integrating fluency with conceptual understanding Children are developing fluency through the practice of multiplication facts. This is being underpinned by conceptual understanding through reference to pictures which illustrate the concept of multiplication. 7
The commutative law for multiplication
Representing 5 x 4 How do the children represent this? Why might it be represented in this way? 9
Representing multiplication in an array Notice how Sam represents the array where the size of the number being multiplied appears in the rows. Is it necessary to be consistent in how the array is orientated? 10
Commutativity Sam says: I want them to understand the commutative law of multiplication that 4 x 3 is the same as 3 x 4 with the same total of 12 . How does the structure of the array support this? 11
The position of the equals sign Notice how the children are confident in using the equals sign at the start of the number sentence and are developing fluency and flexibility. 10 = 5 x 2 10 = 2 x 5 20 = 5 x 4 20 = 4 x 5 12
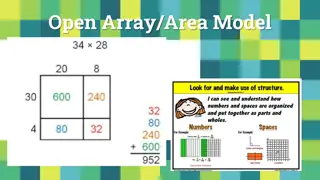
Use of place value counters Notice how the place value counters: Enable the children to represent 34; Support construction of the array; Support understanding the grid method. 14
Moving from grid to a column method
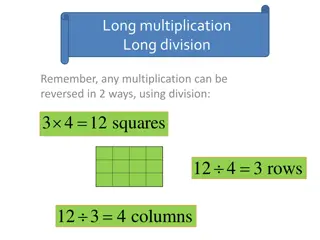
Linking the grid method and formal algorithm The grid method The formal algorithm 246 x 200 40 6 x 37 30 6000 1200 180 6000+1200+180 = 7380 7380 7 1400 280 42 1400+280+42 = 1722 1722 Answer 246x37 = 9102 9102 Source : Good practice in primary mathematics: evidence from 20 successful schools Nov 2011 Ofsted Notice how the order of the numbers in the grid reflects the order of the numbers on the formal algorithm. Consider how the teacher in the video supports children in transferring conceptual understanding from the grid to the formal algorithm. How does this support the development of fluency? 16
Whats the same? What s different ? How does asking the question What s the same, what s different? support children in moving from the grid to the column method? Notice also the choice of numbers: there is no repetition in the digits in order that children can match the same numbers in the grid method and formal algorithm. 17