Understanding Forces Applied at an Angle on Inclined Planes

Slide Note

Exploring the concept of forces applied at angles other than 90 degrees on inclined planes, the process involves resolving forces into component vectors, finding net forces in each direction, writing force equations (Fnet = ma), and solving for normal force and acceleration in practical scenarios like Luke Skywalker pulling a sled. The steps include drawing a free-body diagram, resolving forces into components, and moving on to the next calculations.

talitha Follow

Uploaded on Aug 21, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

E N D

Presentation Transcript

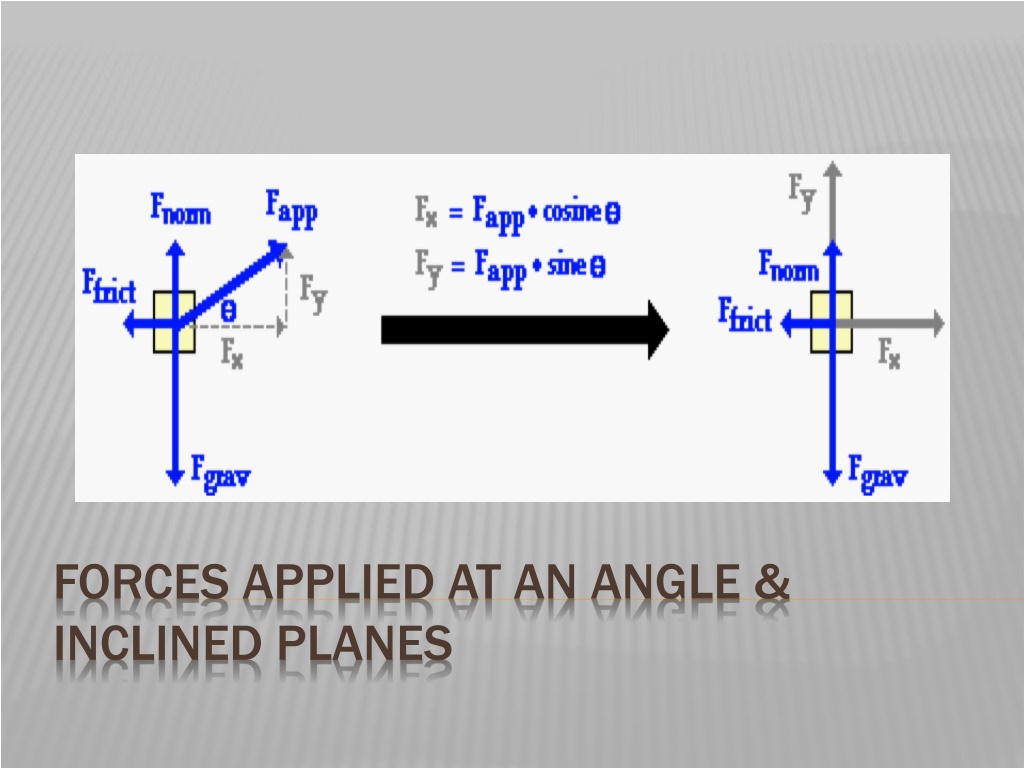
FORCES APPLIED AT AN ANGLE & INCLINED PLANES

FORCES APPLIED AT AN ANGLE When forces are applied at angles other than 90o,we need to resolve the force into its component vectors. Then, we find the net force in each direction, write our force equations (Fnet= ma), and solve.

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. What do we do first? What do we do first?

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. What do we do first? What do we do first? Draw a free Draw a free- -body diagram. body diagram.

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. Now what? Now what?

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. Now what? Now what? Resolve F into components Resolve F into components

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. What next? What next?

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. Add the forces in each direction the horizontal? In the vertical? each direction. What should the forces equal in

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. Add the forces in each direction the horizontal? Unbalanced Fnet = ma In the vertical? Fnet = 0. each direction. What should the forces equal in

FORCES AT AN ANGLE WE DO Luke Skywalker starts to pull a sled with Princess Leia across a large ice pond with the force of 100 N at an angle of 30.0 with the horizontal. Find normal force and initial acceleration if the weight of sled and Princess Leia is 800 N and the friction force is 40 N. mg = 800 N m = 80 kg F = 100 N Ffr = 40 N Horizontal direction: F cos Ffr= ma 86.6 40 = 80 a a = 0.58 m/s2 vertical direction : F sin + Fn- mg = 0 50 + Fn= 800 Fn= 750 N

FORCES AT AN ANGLE YOU DO 1. A box of books weighing 325 N moves with a constant velocity across the floor when it is pushed with a force of 425 N exerted downward at an angle of 35.2 degrees below the horizontal. Find the coefficient of friction between the box and the floor. 2. Two forces act on a 4.5-kg block resting on a frictionless surface as shown. What is the magnitude of the horizontal acceleration of the block?

FORCES AT AN ANGLE YOU DO 1. A box of books weighing 325 N moves with a constant velocity across the floor when it is pushed with a force of 425 N exerted downward at an angle of 35.2 degrees below the horizontal. Find the coefficient of friction between the box and the floor. Constant velocity means no acceleration, which means that the forces in ALL directions are balanced. Ff = 425 cos (35.2) = 361.7 N Ff = sFn Fn = mg + 425 sin (35.2) = 325 N + 425 sin(35.2) Fn = 548.2 N s = 0.66

FORCES AT AN ANGLE YOU DO 2. Two forces act on a 4.5-kg block resting on a frictionless surface as shown. What is the magnitude of the horizontal acceleration of the block? Resolve into components, Add the forces, then find Fnet = ma. 3.7 N + 5.9 N cos 43 = Fnet = 8.3 N a = Fnet / m = 8 .3 N / 4.5 kg = 1.8 m/s2

Draw a free-body diagram for a block accelerating down a ramp.

FORCES ON AN INCLINED PLANE Fn Ffr Oh no! This will be ugly! a We will have to resolve Fn, Ffr, Fnet, and a into components!!! mg Or will we?

FORCES ON AN INCLINED PLANE Fn y Ffr Solution: Choose a more convenient coordinate system! x a Make x be parallel to incline and y be perpendicular. mg Now, only mg has to be resolved into components. Motion and all the other forces will be in the x or y direction.

FORCES ON AN INCLINED PLANE The only force that we have to resolve into components is weight Fn Ffr a y mg x

FORCES ON AN INCLINED PLANE The only force that we have to resolve into components is weight Notice that the angle for resolving mg is the same as the angle of the incline Fn Ffr a y mg x

Resolve vector mg into two components. Now instead of three forces, we have four forces Fn Ffr direction perpendicular to the incline: Fnet= ma = 0 Fn= mg cos

Resolve vector mg into two components. Now instead of three forces, we have four forces Fn Write the Fnetequations direction perpendicular to the incline: Ffr Fnet= ma = 0 Fn= mg cos force pressing the object into the surface is not full weight mg, but only part of it, So the normal force acting on the object is only part of full weight mg: Fn= mg cos

Resolve vector mg into two components. Now instead of three forces, we have four forces Fn Ffr direction parallel to the incline: Fnet= ma Fnet= Ff mg sin = ma The force that causes acceleration downward is only part of the full force of gravity. Greater acceleration the steeper the slope. If the incline = 0, then there is no horizontal movement due to gravity.

INCLINED PLANE WE DO A cute bear, m = 60 kg, is sliding down an iced incline 300. The ice can support up to 550 N. Will bear fall through the ice? If the coefficient of the friction is 0.115, what is the acceleration of the bear? What s my strategy??

INCLINED PLANE WE DO A cute bear, m = 60 kg, is sliding down an iced incline 300. The ice can support up to 550 N. Will bear fall through the ice? If the coefficient of the friction is 0.115, what is the acceleration of the bear? What s my strategy?? 1) Draw the free-body diagram 2) Choose a coordinate system with x parallel to incline 3) Resolve mg into components 4) Add vectors perpendicular to plane and set Fnet = ma = 0. 5) Add vectors parallel to plane and set Fnet = ma.

INCLINED PLANE WE DO A cute bear, m = 60 kg, is sliding down an iced incline 300. The ice can support up to 550 N. Will bear fall through the ice? If the coefficient of the friction is 0.115, what is the acceleration of the bear? m = 60 kg = 300 = 0.115 g = 10 m/s2 Perpendicular direction: Fnet= ma a = 0 Fn- mg cos = 0 Fn= 520 N < 550 N ice can support him, but he should not eat too much Parallel direction: Fnet= ma mg sin Ffr= ma Ffr= Fn = 60 N 300 60 = 60 a a = 4 m/s2 cute bear is speeding up!!!!

INCLINED PLANE YOU DO 3. A block weighing 15.0 newtons is on a ramp inclined at 40.0 to the horizontal. A 3.0 Newton force of friction, Ff , acts on the block as it is pulled up the ramp at constant velocity with force F, which is parallel to the ramp. Find F. 4. A 75 kg box slides down a ramp inclined at 25O with an acceleration of 3.60 m/s2. a) Find the coefficient of friction. b) What acceleration would a 175 kg box have on this ramp?

INCLINED PLANE YOU DO 3. A block weighing 15.0 newtons is on a ramp inclined at 40.0 to the horizontal. A 3.0 Newton force of friction, Ff , acts on the block as it is pulled up the ramp at constant velocity with force F, which is parallel to the ramp. Find F. Constant velocity = no acceleration. This means that forces in parallel to the inclined plane are also balanced. Ff = F F = 12.6 N

INCLINED PLANE YOU DO 4. A 75 kg box slides down a ramp inclined at 25O with an acceleration of 3.60 m/s2. a) Find the coefficient of friction. b) What acceleration would a 175 kg box have on this ramp? Fnet = mg sin 25 Ff = ma Ff = mg sin 25 ma = 40.6 N Ff = s Fn s = Ff / Fn = 40.6 / mgcos25 = 0.06 a = (mg sin 25 Ff ) / m =