Whole Numbers and Basic Properties
Whole numbers are a collection that includes natural numbers and zero. They are denoted by the letter W and start from 0, 1, 2, 3, 4, 5, 6, and so on. The successor of a whole number is obtained by adding 1, and the predecessor is obtained by subtracting 1 (except for 0). The number line begins at 0, with larger numbers towards the right. Various properties such as closure, commutative, associative, distributive, and identity hold true for addition and multiplication on whole numbers.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
THE NATURAL NUMBERS ALONG WITH ZERO FORM THE COLLECTION OF WHOLE NUMBERS IT IS DENOTED BY W IT STARTS FROM 0,1,2,3,4,5,6 .
IF WE ADD 1 TO WHOLE NUMBER THEN WE GET SUCCESSOR SUCCESSOR 2 IS 2+1=3 3 IS SUCCESSOR OF 2 IF WE SUBTRACT 1 WHOLE NUMBER EXCEPT 0 WE GET PREDESSOR PREDESSOR OF 4 IS 4-1=3 3 IS PREDESSOR OF 4
RIGHT THE VALUE LARGER LEFT TO MOVE FROM
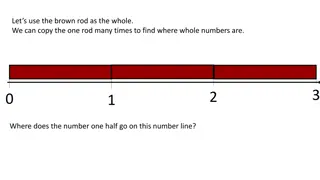
THE NUMBER LINE STARTS FROM 0 LARGER NUMBER WILL BE RIGHT SIDE OF SMALLER NUMBER THERE WILL BE NO PREDESSOR OF 0
1. CLOSUR PROPERTY 2. COMMUTATIVE PROPERTY 3. ASSOCIATIVE PROTERTY 4. DISTRIBUTIVE PROPERTY 5. IDENTITY PROPERTY THE ABOVE PROPERTIES ARE TRUE ONLY FOR ADDITION AND MULTIPLICATION ON WHOLE NUMBERS