Understanding Vertical Motion and Gravity in Kinematics
Explore the principles of vertical motion and gravity in kinematics through scenarios involving throwing objects, free-fall motion, and calculating heights. Learn how to model vertical motion with acceleration due to gravity, find maximum heights of thrown objects, solve extended problems, and understand the changes in velocity during motion. Dive into concepts such as acceleration due to gravity, velocity-time graphs, and displacement-time graphs to deepen your understanding of kinematics.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Kinematics Vertical motion
KINEMATICS 2 KUS objectives BAT Set up a model of vertical motion with acceleration due to gravity BAT Find the high point of a thrown object or distance travelled BAT Solve extended problems Starter: Find each missing variable s = ? u = ? v = 12 ms-1 a = -9.8 ms-2 t = 6 seconds s = 20 m u = 5 ms-1 v = ? a = 5 ms-1 t = ?
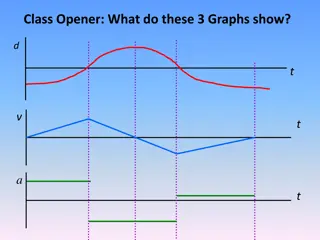
Leroy throws a ball vertically upwards and catches it when it returns Describe how the velocity of the ball changes during its motion. What is the velocity of the ball when it is at its maximum height How does the velocity of the ball when Leroy catches it relates to when he threw it? Sketch a velocity-time graph for the motion of the ball Sketch a displacement-time graph for the motion of the ball, where the displacement is measured upwards from Leroy s hand
Vertical motion under gravity The acceleration of a falling object is caused by gravity This acceleration is known as the acceleration due to gravity, g, and is approximately 9.8ms-2. The motion of the object is in a vertical straight line with constant acceleration, 9.8ms-2, so the constant acceleration equations can be applied. This assumes that the object is falling freely and air resistance can be ignored.
WB9 A stone is dropped off the edge of a cliff. It hits the water after 4 seconds. Calculate the height of the cliff above the water. ? = ? + ?? ? + ? ? = s ? = 0 ? = ? = 9.8 ? = 4 ? = ? 2 ? = ?? +1 ?2= ?2+ 2?? ? = ?? 1 2??2 ? = ?? +1 2??2 2??2 ? = (0) +1 2(9.8)(4)2 ? = 78.4 ? How would apply this to find the height of a well?
? = ? + ?? ? + ? WB10 A marble falls off a shelf which is 1.6 m above the floor. Find: a) the time it takes to reach the floor b) The speed with which it will reach the floor ? = ? 2 ? = ?? +1 ?2= ?2+ 2?? ? = ?? 1 2??2 2??2 ? = 1.6 ? = 0 ? = ? ? = 9.8 ? = ? = = = + 1 2 s ut 0 16 1at 2 8 . 9 . 0 = + 2 6 . 1 t t = = + 2 2 2 v v v as 8 . 9 36 . 31 6 . 5 = u 0 2 2 327 + 6 . 1 2 2 49 2= v 4 = = . 0 571 t 7
? = ? + ?? ? + ? WB11 A marble is catapulted vertically upwards with a velocity of 24.5 ms-1. Modelling the marble as a particle moving under gravity alone, find for how long its height exceeds 29.4 m ? = ? 2 ? = ?? +1 ?2= ?2+ 2?? ? = ?? 1 2??2 2??2 ? = 29.4 ? = 24.5 ? = ? = 9.8 ? = ? = + 2 s 4 . ut = 1at 5 . 24 5 + t Why is acceleration negative? 2 + ) 8 . 9 2 29 ( t t 1 2 Can you simplify? + = = 2 9 . 4 24 5 . 29 0 4 . 0 t t 2 6 t = = 2 3 t or t So the marble is above 29.4m for 1 second
WB12a A particle P is projected upwards from a point O with a speed of 28 ms-1. Find: a) The greatest height above O reached by P b) The total time before P returns to O c) The total distance travelled by the particle on return to O Why is velocity zero at the greatest height ? ? s = + 2 2 2 v u as 28 u What assumptions are made in this model? 0 v = + 2 0 28 2 ( ) 8 . 9 s 8 . 9 a t = 40 s
= + s v u at u = + 2 s ut at 1 2 WB12bc A particle P is projected upwards from a point O with a speed of 28 ms-1. Find: a) The greatest height above O reached by P b) The total time before P returns to O c) The total distance travelled by the particle on return to O v + u v = s t a 2 = + t 2 2 2 v u as = + v 28 u at + s Why is v = -28 ? 28 u = = t ) 8 . 9 28 ( 28 v The motion is symmetrical 8 . 9 . 5 74 a t ? t c) Distance is twice the distance to the greatest height = 80 m
ACTIVITY 7 Throw a ball vertically Max height, velocity = ? Aim: Find a model for the projectile motion of a ball vertically st a rt Ball metre rule / measure tape stopwatches Equipment: 5 m Throw a ball in the air and time how long it takes to return to the same height What is the velocity at the greatest height reached by the ball? What is the time taken to reach the greatest height? What assumptions can you make in this model? What are the displacement (s), acceleration (a) and time (t) for the vertical motion of the ball? Calculate the height the ball reaches and its final velocity (use the constant acceleration equations) Repeat and collect some results What problems are there with this model?
BATSet up a model of vertical motion with acceleration due to gravity BAT find the high point of a thrown object or distance travelled BATSolve extended problems One thing I will do For the next lesson . One thing I need to remember for next lesson . One thing I understood well is . Plenary pyramid