Understanding Topological Complexity Estimations and Regularity of Spaces

Slide Note

Discussion on the varying estimates of topological complexity for wedges, closed manifolds, and other spaces, along with the analysis of TC-regularity. This includes contrasting estimates, proofs, and examples of TC regularity in different spaces like spheres and Lie groups.

ervi_on Follow

Uploaded on Nov 19, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

E N D

Presentation Transcript

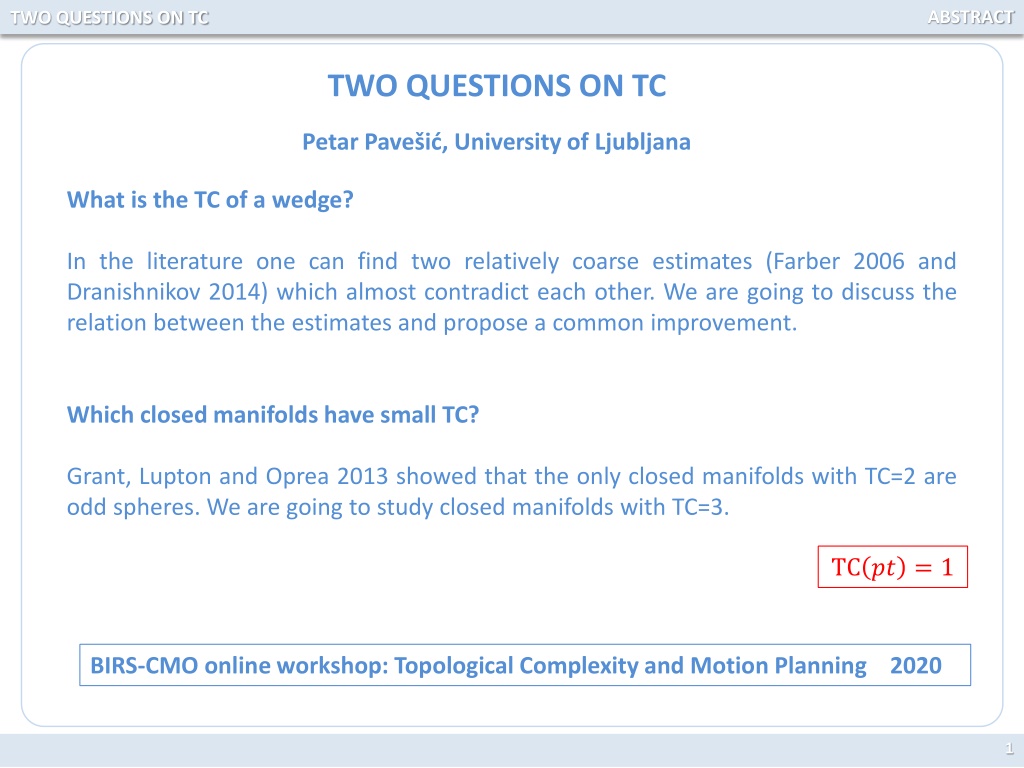
ABSTRACT TWO QUESTIONS ON TC TWO QUESTIONS ON TC Petar Pave i , University of Ljubljana What is the TC of a wedge? In the literature one can find two relatively coarse estimates (Farber 2006 and Dranishnikov 2014) which almost contradict each other. We are going to discuss the relation between the estimates and propose a common improvement. Which closed manifolds have small TC? Grant, Lupton and Oprea 2013 showed that the only closed manifolds with TC=2 are odd spheres. We are going to study closed manifolds with TC=3. TC ?? = 1 BIRS-CMO online workshop: Topological Complexity and Motion Planning 2020 1

?? ? ? TWO QUESTIONS ON TC Estimates of TC ? ? : max {TC ? ,TC(?)} TC(? ?) max{TC ? ,TC ? ,cat ? + cat ? 1} (Farber, Topology of robot motion planning, 2006) max {TC ? ,TC ? ,cat(? ?)} TC(? ?) TC ? + TC ? + 1 (Dranishnikov, Topological complexity of wedges and covering maps, 2014) 8 15 TC ??7 ??7: 15 17 12 13 TC F(?2,7) F(?2,7) : 13 25 ?,? Lie groups cat ? ? TC ? ? cat ? + cat ? 1 2

?? ? ? TWO QUESTIONS ON TC Dranishnikov s proof of TC ? ? TC ? + TC ? + 1: Represent ? ? ? ? as Find pointed (monoidal) motion plans for ?,? with at most TC ? + 1,TC ? + 1 charts. ? ? ? ? If necessary, adjust motion plans so that they are stationary during first or second half time on ? ? and ? ? . ? ?0 ?0 ?0 ? ? Split ? ? and ? ? according to intersections with slices and define motion plans on each part by the rule first half time first component, second half time second component . ? ? ? ? So defined motion plans coincide on intersections along slices in ? ? ? ? determined by the basepoint (?0,?0) so we may collect them as in the diagram. In the worst case, we need TC ? + TC ? + 1 charts. 3

?? ? ? TWO QUESTIONS ON TC In the best case ?,? admit pointed motion plans with TC ? ,TC ? rules, and the corresponding domains have at most cat(?) non-empty intersections with ? ?0, ?0 ? and at most cat(?) non-empty intersections with ? ?0, ?0 ?. Then we may repeat the previous argument, but the collection diagram has less domains. ? ? ? ? By suitably grouping together we obtain a motion plan with max {TC ? ,TC ? ,cat ? + cat ? 1} domains. ? ? ? ? A motion plan for ? is TC-regular, if it is pointed (i.e., monoidal), and if the domains have cat(?) non-empty intersections with slices ? ?0, ?0 ?. A space ? is TC-regular if it is homotopy equivalent to a space that admits a TC-regular motion plan. If ?,? are TC-regular spaces, then max {TC ? ,TC ? ,cat(? ?)} TC(? ?) max {TC ? ,TC ? ,cat ? + cat ? 1} 4

?? ? ? TWO QUESTIONS ON TC Spheres are TC-regular. (by direct inspection) Lie groups are TC-regular. (Dranishnikov 2014) TC ? = 2 cat ? 1 >dim X +1 conn(?) ? is TC-regular. (apply Dranishnikov 2014) (includes surfaces, complex/quaternionic projective spaces) ?(??,?) are TC-regular. (apply Mas-Ku, Torres-Giese 2015) ?,? TC-regular, TC ? ? = TC ? + TC ? 1 ? ? is TC-regular. Are all spaces TC-regular? 5

MANIFOLDS WITH SMALL TC TWO QUESTIONS ON TC Manifolds with small TC Topological complexity is studied for arbitrary topological spaces but the most important cases are still manifolds and in particular closed manifolds. Examples show that TC is, in a sense, a more restrictive invariant than cat: cat ? = 1 TC ? = 1 ? ??. cat ? = 2 ? is a co-H-space (equivalently: a retract of a suspension) TC ? = 2 ? ?2? 1 (Grant, Lupton, Oprea 2013) cat ? = 2, (? closed manifold) ? is a sphere TC ? = 2, (? closed manifold) ? is an odd-dimensional sphere cat ? = 3, (? closed manifold) ?1(?) is free (Dranishnikov, Katz, Rudyak 2008) not much is known in general, e.g. all 1-connected 4-manifolds have cat=3 We will study closed manifolds with TC=3. 6

MANIFOLDS WITH SMALL TC TWO QUESTIONS ON TC Examples with TC ? = 3: even-dimensional spheres, products of two odd-dimensional spheres (because TC ? ? TC ? + TC ? 1). The only surfaces with TC=3 are the 2-sphere and the torus. standing assumption: ? is a closed orientable ?-dimensional manifold, ? 3 TC ? = 3 cat ? 3 ?1(?) is free (Dranishnikov, Katz, Rudyak) rank ?1? = 0 Cases: rank ?1? = 1 rank ?1? 2 7

MANIFOLDS WITH SMALL TC TWO QUESTIONS ON TC rank ?1? 2 Consider non-singular pairing ?1? ?? 1? ??? and find elements ?,? ?1? , ? ,? ?? 1? s.t. ?? = ?? = ?, ?? = ?? = 0 Then ? 1 1 ? ? 1 1 ? therefore TC ? > 4. ? 1 1 ? ? 1 1 ? = 2? ? 0, rank ?1? = 1 As before, find elements ? ?1? , ? ?? 1? s.t. ?? = ?. If (? 1) even, then ? 1 1 ? ? 1 1 ?2= 2 ? ? ? ? 0, therefore TC ? > 3. If (? 1) odd and there is a non-trivial ? ??? ,2 < ? < ? 1, then ? 1 1 ? ? 1 1 ? ? 1 1 ? = ? ? ? ? ?? ? ? ?? 0 Conclusion: ?1? = and TC ? = 3 implies ? ? ?1,??,? odd. 8

MANIFOLDS WITH SMALL TC TWO QUESTIONS ON TC denote ? ?;? ? 0,???(?;?) ? simply connected Similar as above, ?1? trivial and TC ? = 3 implies ? ? ??,??, 1 < ? ? < ? 1, ?,? odd ? ?; 0 ? ?; = 0, ? ?; ? 0, ? odd ? > 1 minimal s.t. ??(?; ) has ?-torsion; then by UCT and Poincare duality ???; ? 0 for ? = ?,? + 1,? ?,? ? 1. Thus ???; ? 0 in at least three dimensions, and then TC ? > 3, unless ? = 2? + 1, and then one is even-dimensional, so again TC ? > 3. ? ?; = 0, ? ?; ? = 0, ? odd, ? ?; 2 0 Similar as above, except that ? = 2? + 1 does not imply TC ? > 3. Then TC ? = 3 implies ? ?; 2 ??,??+1 2. Then TC ? = 3 implies ? ? ??,? even ? ?;? = 0 for all ? 9

MANIFOLDS WITH SMALL TC TWO QUESTIONS ON TC ? is a closed orientable ?-dimensional manifold with TC ? 3. Then ?1? is free and one of the following alternatives hold: - ? ? ?? - ? ? ??,??, 1 ? ?, ?,? odd - ??? = 2, ??? = 0,? 0,?,?, ? ?; 2 ??,??+1 2 Manifolds with TC 3 ? ? ?? ? is a sphere ? ? ?1,?? 1 ? ?1 ?? 1 ? ?1 ?? 1 (Kreck-L ck 2009) ? ? ??,??, 1 < ? ?, ?,? odd examples: ?? ??, ?? 3 ?3,?5 , ?? 2 ?3,?7 examples? homogeneous spaces ?? ? + 2 /?? ? , ??-bundles over ??, unions of two ?? ?? ? along ?? ?? ? 1, Wu-manifold ?? 3 /?? 3 ( ?2,?3 2 ) Problem: find methods to determine TC of examples? 10