Understanding the Metric System in Measurements
The metric system uses prefixes to represent larger or smaller units, such as kilo, hecto, deka, deci, centi, and milli. It includes common mass (gram, kilogram, milligram) and volume units (liter, milliliter) with examples and operations to find volumes and add measurements.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
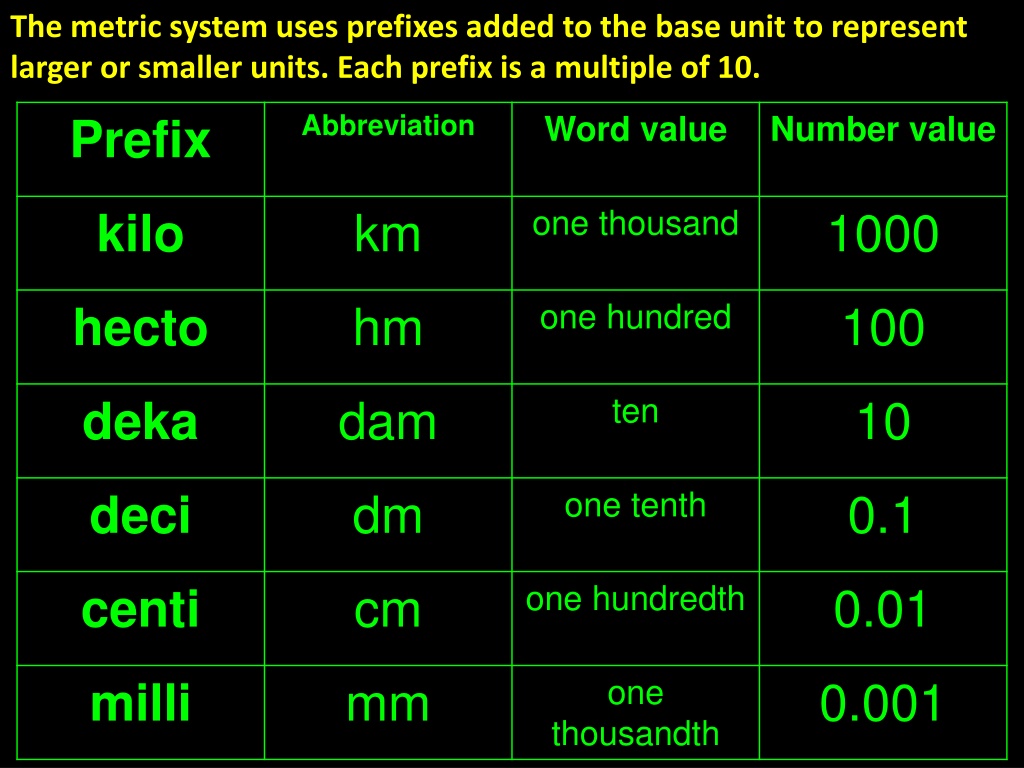
The metric system uses prefixes added to the base unit to represent larger or smaller units. Each prefix is a multiple of 10. Abbreviation Word value Number value Prefix one thousand km 1000 kilo one hundred hm 100 hecto ten dam 10 deka one tenth dm 0.1 deci one hundredth cm 0.01 centi one mm 0.001 milli thousandth
Most Common Mass Units in Metric System Length Units in Metric System kilometer hectometer dekameter meter decimeter centimeter millimeter kilogram gram milligram Most Common Volume Units in Metric System liter milliliter
0 cm 7.55 cm
.5ml 1ml 5ml 10ml 2ml
A. 48 ml B. 45 ml C. 38 ml D. 27 ml E. 18 ml F. 7 ml
38 ml - 32 ml 6 ml The volume of the fish is 6 ml.
260 ml - 200 ml 60 ml The volume of the pebble is 60 ml.
Finding volume using the mathematical formula: Volume = length X width X height Volume = l X w X h height length
5 cm 4 cm 9 cm Volume = ll X X w w X X h h Volume = Volume = Volume = 9cm 9cm X X 4cm 4cm X X 5cm 5cm Volume = Volume = 180 cm 180 cm3 3
60 g 100 g 5.3 g Add the numbers from all three beams. Answer is 165.3 g
10 g 200 g 6.5 g Answer is 216.5 g
70 g 300 g 3.35 g Answer is 373.35 g