Understanding Quantitative and Qualitative Assessment using ROC Curve Analysis
This work delves into the importance of Receiver Operating Characteristic (ROC) curves in assessing and comparing predictive models. The content covers the graphical representation of sensitivity, specificity, and false positive rates, aiding in model evaluation. Examples and visual aids provide insights into susceptibility mapping and dataset selection for ROC analysis.
- ROC Curve Analysis
- Quantitative Assessment
- Qualitative Assessment
- Model Evaluation
- Data Visualization
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
QUANTITATIVE & QUALITATIVE ASSESSMENT ROC Curve Analysis, and Visual Inspection This work is supported by the National Science Foundation s Directorate for Education and Human Resources (TUES-1245025, IUSE- 1612248, IUSE-1725347). Version: 05 25, 2018 Questions, contact education-AT-unavco.org
DISCLAIMER To simplify the process for us, we assume each landslide point translates to a single landslide pixel. This material can be a bit confusing! Ask questions, and take careful notes!
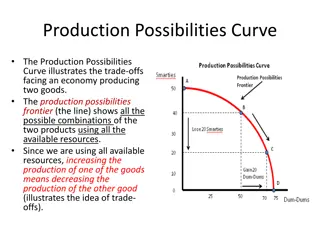
QUANTITATIVE ASSESSMENT Receiver Operating Characteristic (ROC) Curves Useful tool in evaluating and comparing predictive models. Graphical way to show sensitivity and 1-specificity for every possible cut-off for a test. Chart Title Sensitivity (True Positive Rate) probability of predicting that a real positive as a positive. y = 0.3382x4 + 0.1256x3 - 2.0268x2 + 2.5605x + 0.002 1.2 1 True Positive Rate 0.8 0.6 1-Specificity (False Positive Rate) Probability of predicting that a real negative will be a positive. 0.4 0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 What does this mean? False Positive Rate
EXAMPLE The image to the left is a final susceptibility map that was generated using the Arizona dataset for a subregion. The image was classified into 5 categories (see legend). The cutoffs were determined using natural jenks. LEGEND Red Very High Orange High Yellow Moderate Light Green Low Green Very Low
EXAMPLE We use the XXLandslides25 point shapefile to run an ROC analysis. Why do we use this dataset rather than XXLandslides75? LEGEND Red Very High Orange High Yellow Moderate Light Green Low Green Very Low There are 918 landslides points in the XXLandslides25 point shapefile for this example. Things we need to do an ROC analysis: A number of XXLandslides25 above a cutoff in the classified final map. A + B total number of landslides in XXLandslides25 C number of pixels in total area above a cutoff minus A in the final susceptibility map image C + D total number of pixels in image NOTE: The XX represents Az for Arizona, or PR for Puerto Rico.
Chart Title y = 0.3382x4 + 0.1256x3 - 2.0268x2 + 2.5605x + 0.002 1.2 1 0.8 True Positive Rate 0.6 0.4 0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 False Positive Rate
EXAMPLE STEP 1: LEGEND Red Very High Orange High Yellow Moderate Light Green Low Green Very Low We assume an unlisted cutoff below the most minimum pixel value (below Very Low). This forces an approximate one-one point. Results for STEP 1: A 918. There are 918 out of 918 landslides predicted as landslides according to this extremely low cutoff. A + B 918 C 132,614 (133,532-918). This is the number of pixels identified as a positive, when they are in fact negatives. C + D 133,532 total pixels in image TPR = A/(A+B) FPR = C/(C+D)
Chart Title y = 0.3382x4 + 0.1256x3 - 2.0268x2 + 2.5605x + 0.002 1.2 1 0.8 True Positive Rate 0.6 0.4 0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 False Positive Rate
EXAMPLE STEP 2: LEGEND Red Very High Orange High Yellow Moderate Light Green Low Green Very Low We move to the cutoff between Very Low/Low. Results for STEP 2: A 876. There are 876 out of 918 landslides predicted as landslides according to this extremely low cutoff. A + B 918 C 109,889. This is the number of pixels ABOVE the cutoff identified as a positive, when they are in fact negatives. We ignore all the pixels/landslides below this cutoff. C + D 133,532 total pixels in image. TPR = A/(A+B) FPR = C/(C+D)
EXAMPLE Continue repeating these steps for each individual cutoff. LEGEND Red Very High Orange High Yellow Moderate Light Green Low Green Very Low Now, where do we go from here? 1. Fit a trendline (polynomial) to your points. 2. Display the trendline equation. 3. Copy the equation into an integral calculator for the interval from 0-1. This results in the area under curve (AUC) value.
WHAT DOESTHE AUC MEAN? A value less than 0.5 should not be possible. Values from 0.5 0.6 mean the model is not a good predictor. Values from 0.6 0.7 mean the model is OK as a predictor, but not ideal. Values 0.7- 0.8 mean the model is a good predictor. Values in excess of 0.8 mean the model is a great predictor. A value of 1.0 means the model is an excellent predictor.
Chart Title y = 0.3382x4 + 0.1256x3 - 2.0268x2 + 2.5605x + 0.002 1.2 How good of a predictor is this model? Should this model be used as a predictor? 1 0.8 True Positive Rate 0.6 AUC = 0.706 0.4 0.2 0 0 0.2 0.4 0.6 0.8 1 1.2 False Positive Rate
QUALITATIVE ANALYSIS The AUC value may sometimes suggest a good predictor, but qualitative analysis may suggest otherwise. Based on the final susceptibility map to the right, would this qualitatively be a good, or bad model? Why or why not?