Understanding Metric Systems and Significant Figures
Scientists worldwide use the SI system to communicate clearly, based on units like meter, gram, and liter. Learn about base and derived units, SI base units like second and kilogram, and derived units like volume. Discover which unit (millimeter, centimeter, meter, or kilometer) to use for different measurements like paper thickness, pencil length, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Metric Systems and Significant Figures Mrs. Charniauskaya
Metric System Scientists all over the world use the same system of units so they can communicate information clearly This system is called Syst me Internationale d Unit s (SI) Metric measurement is based on the number of 10 and makes calculations easier.
Base Metric Units Measurement Unit of Measurement Length Meter (m) Mass Gram (g) Second (s) Time Volume Liter (L or l)
What unit (millimeter, centimeter, meter, or kilometer) would be most appropriate for describing the following: a. The thickness of a piece of paper b. The length of your pencil c. The distance from Chicago to L.A. d. The height of the classroom door ___________________ e. The width of a textbook ___________________ f. The height of the flagpole g. The thickness of a penny ________________ _______________________ ________________ ____________________ ____________________
Units According to Syst me Internationale d Unit s (SI) 1960 there are base and derived units. Base unit is based on a object or event in a physical world and is independent of other units. Examples: meter (length of an object); kilogram (mass of an object); second (time and event takes). Derived unit is developed from base units (made of two or more base units). Examples: ? ?, ????? ? ??????(speed); ???? ???, ????? ??????????(density); ???(volume)
Units SI Base Units Quantity Base Unit Time Second (s) Length Meter (m) Mass Kilogram (kg) Temperature Kelvin (K) Amount of substance Mole (mol) Electric Current Ampere (A) Luminous Intensity Candela (cd)
Units Derived Units A unit that is defined by a combination of base unit is called derived unit, Volume is the space occupied by an object. Si Unit m3 Other Unit Used cm3, mL, L Volume Cubic centimeter (cm3) Milliliter (mL or ml) Liter (L or l) 1 cm3= 1 ml
Units: Derived Units Density is how much mass an object has per unit of volume, the degree of compactness of a substance. https://phet.colorado.edu/en/simulation/legacy/density https://phet.colorado.edu/en/simulation/legacy/density Density of an object is equal to its mass divided by its volume. ? =? ? ? ??= ??? ? ? = Units of density are derived from base units of mass and length.
Metric Prefix Metric Prefixes make base unit smaller or larger. Kilo Hecto Deka Base Unit Deci Centi Milli k H Da d c m 1000 100 10 1 0.1 0.01 0.001 103 102 101 100 10-1 10-2 10-3 ???? ? ??? ? ??? ? ? ? ? ? ? ?? ??? ????
Metric Prefixes To explain the range of a measurement, scientists add prefixes to the base units. Prefix Symbol Numerical Value Power of 10 equivalent 103 100 10-1 10-2 10-3 10-6 Kilo k 1000 1 0.1 0.01 0.001 0.000001 Deci Centi Milli Micro d c m Nano n 0.000000001 10-9
Metric Prefixes Kilo- Hecto- Deka- Base Deci- Centi- Milli- Each unit is 10 times larger than the previous one. 1 cm = 10 mm Each unit is 10 times smaller than the previous one. 1 mm = 0.1 cm
Relationship between metric units 1 kg = 1000 g 1 km = 1000 m 1 kL = 1000 L 1g = 10 dg 1 m = 10 dm 1 L = 10 dL 1g = 100 cg 1 m = 100 cm 1 L = 100 cL 1 g = 1000 mg 1 m = 1000 mm 1 L = 1000 mL
What is the length of the blue object? Uncertainty in measurements 1.24 cm? 1.245 cm? 1.25 cm? Which digits are we certain about? Which digit we are uncertain about? A digit that must be estimated is called uncertain. A measurement always has some degree of uncertainty.
Uncertainty in measurements Measurements are performed with instruments. No instrument can read to an infinite number of decimal places.
Significant figures Scientists use significant figures to take into account uncertainty of measurement. In measurements, the significant figures are all the digits that are known, plus a digit that is estimated. 2 sig fig. 3 sig fig.
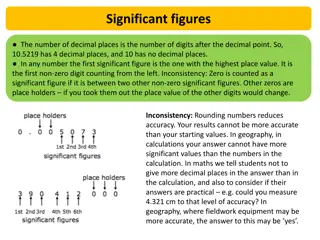
Rules for Counting Significant Figures Nonzero integers always count as significant figures. 3456 has 4 sig figs.
Zeros Leading zeros do not count as significant figures. 0.0486 has 3 sig figs. Leading zeros
Zeros Captive zeros always count as significant figures. 16.07 has 4 sig figs. Captive zero
Zeros Trailing zeros are significant only if the number contains a decimal point. 9.300 has 4 sig figs. Trailing zeros
Zeros Trailing zeros are not significant if the number does not contain a decimal point. 9300 has 2 sig figs. Trailing zeros
There are two situations in which a number has a unlimited number of significant figures: Counted numbers are exact. 27 people in your classroom. 275000 people in a city (all figures are significant) Exactly defined quantities. 1 inch = 2.54 cm 1 h = 60 min
When scientist report measurements values they must report correct number significant figures. The correct volume is 56.0 ml, or 55.9 ml, or 56.1 ml The values of 56 ml or 55.95 ml are incorrect, because of incorrect number of sig. figs.
Honors Chemistry, September 9, 2016 Bell Work: Learning Objective; Be able to perform calculations with the sig. figs. Present as a scientific notation 0.00003506 Present as a standard (expanded) notation Agenda: 7.59 ?? ? Bell Work HW check and review 58674 mL into L Quiz How many sig. figs.: Calculations with sig. figs. 0.000609 Practice 689000
When scientists do the calculations with the measured values they are coming up with the unreasonable number of significant figures. Mass of an object 6.52 g Object s volume is 1.3 cm3 ?=6.52 g 1.3 cm3= ?.??????????????? Does the value for density look reasonable? ? =? ? ??? What do we need to do?
Rounding To round a number, decide how many significant figures the answer should have. It depends On given measurement On type of calculation
Multiplication and Division: # sig figs in the result equals the lowest number of sig figs in the calculation. Mass of an object 6.52 g (3 sig. fig.) Object s volume is 1.3 cm3 (2 sig. fig.) The answer should have 2 sig. figs. ?=6.52 g 1.3 cm3= ?.??????????????? ? =? ? ? ???= 5.0 ???
Rounding Addition and Subtraction: The number of decimal places in the result equals the lowest number of decimal places in the calculation. Lowest number of decimal places 6.8 + 11.934 = 18.734 = 18.7 One decimal place One decimal place
Accuracy and Precision Accuracy refers to how close a measured value is to an accepted value. Precision refers to how close a series of measurements are to one another.
Percent Error Percent error is calculated to know how measured or calculated value is close to accepted (true) value. ????? %????? = ???????? ????? ???% |???????????? ????? ???????? ?????| ???????? ????? %????? = ???%
Percent Composition You have a 100 g mixture of sugar and water. What is percent composition of sugar if there are 20 g of sugar in the mixture? Percent composition % ????????? =???? ?? ? ????????? ???% ????? ????
Measurement is a quantitative observation Measurement always has a number and a unit of measurement 2 dollars 2 cents 2 g 2 kg