Understanding Means and Averages in Mathematics
Learn how to calculate means and averages using real-world examples: sharing counters equally among students, tracking daily vegetable portions, finding the mean of different sets of values, determining missing values in sets, and adjusting sums to meet new mean averages.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
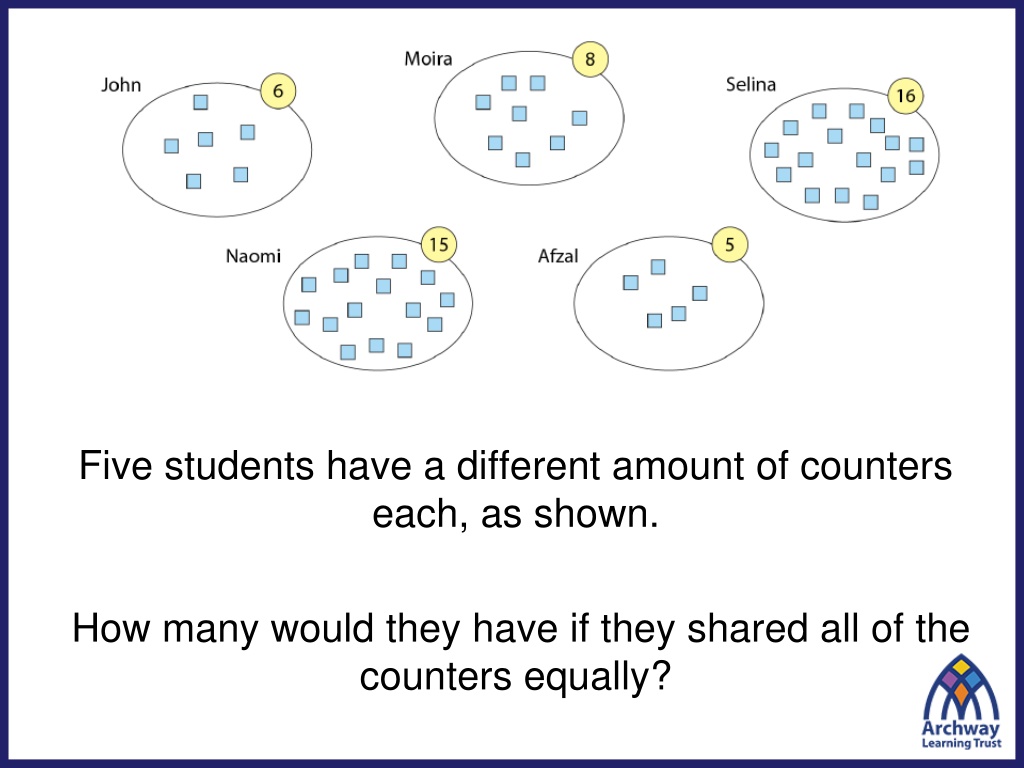
Five students have a different amount of counters each, as shown. How many would they have if they shared all of the counters equally?
An efficient way to solve this problem is to use that: there are 50 counters in total. there are 5 students. Therefore each student would have 10.
The mean average number of counters per student is 10. The calculation of the mean requires three operations: The sum of the data values (eg. 50 counters) The count of the number of data values (eg. 5 students) Then the division of the sum by the count. (eg. 50 5 = 10 counters)
On your whiteboard James wants to improve his diet. For a fortnight he records the number of portions of vegetables he eats each day. What is the mean daily number of portions of vegetables he eats? 0 He eats 42 portions of vegetables (the sum) Over 14 days (the count) The mean average is 42 14 = 3 portions of vegetables per day.
On your whiteboard Find the mean of the following sets of values. a) 6, 6, 6, 6 b) 6, 7, 5, 6 c) 12, 0, 0, 12 d) 4, 5, 7, 8 What is the same? What is different?
On your whiteboard The mean average of the following set of four values is 6. 6, 3, 5, ? What must the sum of the four values be?
On your whiteboard The mean average of the following set of five values is 6. 6, 3, 5, ? What is the missing value?
On your whiteboard The mean of five data values is 6. Another piece of data is included and the mean is now 7. What value of the sixth piece of data?
On your whiteboard The mean of five data values is 6 - five data values must sum to 30 Another piece of data is included and the mean is now 7 - six data values must now sum to 42 What value of the sixth piece of data?
Title: Mean Problems Worked Example The mean age of 4 students is 12 years old. Another student joins the group, aged 16. What is the mean age of the 5 students? Your turn The mean age of 3 students is 15 years old. Another student joins the group, aged 16. What is the mean age of the 4 students? Solution The sum of the ages of the 4 students is: 4 12 = 48 years The sum of the ages of the 5 students: 48 + 16 = 64 ????? The mean average of the 5 students is: 64 5 = 12.8 ????? Solution The sum of the ages of the 3 students is: 3 15 = 45 years The sum of the ages of the 4 students: 45 + 16 = 61 ????? The mean average of the 5 students is: 61 4 = 15.25 ?????
Independent Practise The mean age of 2 girls is 8 years old. Another girl joins, age 5. What is the mean age of the 3 girls? The mean number of goals scored by 3 players is 18. Another player joins, having scored 6 goals. What is the mean number of goals scored by the 4 players? The mean heights of 24 men is 1.64m. Another man has a height of 1.89m. What is the mean height of the 25 boys? The mean of 3 numbers is 15. Another number is added. The mean is now 12. What number was added? The mean of 9 numbers is 1.5. Another number is added. The mean is now 1.6. What number was added? The mean of 5 numbers is 8. Another number is added. The mean is now 6. What number was added? The mean of 5 numbers is 30. A number is taken away. The mean of the 4 remaining numbers is 25. What number was taken away? The mean age of a team of 25 players is 26. One of the players, age 20, is sold. What is now the mean age of the team? The mean age of 9 boys is 10. The mean age of 9 girls is 15. What is the mean age of all the boys and girls? 4 adults and 6 children have a mean age of 21.8 The adults have a mean age of 35. What is the mean age of the children? Two parents have 3 daughters and 2 sons. The mean age of the family is 18. The mean age of the daughters is 13. The mean age of the sons is 10. The mother is 3 years younger than the father. How old is the father? Team A consists of 13 players with a mean age of 26. Team B has 11 players with a mean of 28. A player leaves Team A to join Team B. The new mean of Team A is 26.5 What is the new mean of Team B?
Mark/Correct your work The mean age of 2 girls is 8. Another girl joins, age 5. What is the mean age of the 3 girls? 7 The mean number of goals scored by 3 players is 18. Another player joins, having scored 6 goals. What is the mean number of goals scored by the 4 players? 15 The mean heights of 24 men is 1.64m. Another man has a height of 1.89m. What is the mean height of the 25 boys? 1.65 The mean of 3 numbers is 15. Another number is added. The mean is now 12. What number was added? The mean of 9 numbers is 1.5. Another number is added. The mean is now 1.6. What number was added? 2.5 The mean of 5 numbers is 8. Another number is added. The mean is now 6. What number was added? -4 3 The mean of 5 numbers is 30. A number is taken away. The mean of the 4 remaining numbers is 25. What number was taken away? 50 The mean age of a team of 25 players is 26. One of the players, age 20, is sold. What is now the mean age of the team? 26.2 5 The mean age of 9 boys is 10. The mean age of 9 girls is 15. What is the mean age of all the boys and girls? 12.5 4 adults and 6 children have a mean age of 21.8 The adults have a mean age of 35. What is the mean age of the children? 13 Two parents have 3 daughters and 2 sons. The mean age of the family is 18. The mean age of the daughters is 13. The mean age of the sons is 10. The mother is 3 years younger than the father. How old is the father? 35 Team A consists of 13 players with a mean age of 26. Team B has 11 players with a mean of 28. A player leaves Team A to join Team B. The new mean of Team A is 26.5 What is the new mean of Team B? 27.3
Challenge Five circles have radii (in cm) as shown. Some of the circles have their radii changed. The new mean radius increases by 7 but the range and the median stay the same. What are the new radii?