Understanding Averages in Mathematics
Explore the concepts of mean, mode, and median, along with practical examples and puzzles involving these averages. Learn the importance of each average in different contexts and how to calculate them effectively. Dive into frequency tables and range calculations to deepen your understanding of statistical measures. Enhance your mathematical skills with engaging exercises and worksheets provided by Dr. J. Frost.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
KS3 Mean, Mode, Range Dr J Frost (jfrost@tiffin.kingston.sch.uk) Last modified: 12th October 2013
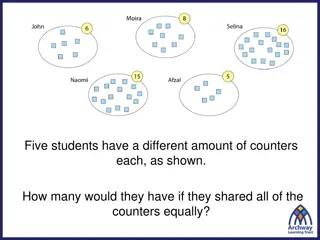
Averages There are different averages: some are more meaningful than others depending on the context. What is the average number of ears in the world human population? ? The mode represents the most common value. Modal number of ears: 2 ? The mode (the modal average ) ? The median represents the middle value. Median number of ears: 2 ? The median The mean takes into account all values. We add up the values and divide by the number of values. Mean number of ears: 1.99999 The mean ?
Averages There are different averages: some are more meaningful than others depending on the context. The mode tends to be a good average when we want to give an indication of the value that is most common. The mode (the modal average ) Median is often good because it makes it easier to tell whether a value is in the top 50% or the bottom 50%. It s also less sensitive to extreme values. The median The mean is the best average to use if we want to take all the values into account. The mean Salaries of people in the room: 13,000 18,000 24,000 25,500 26,000 32,000 45,000 1,200,000 What would the best average be here?
Averages Copy these numbers down, and work out the mean, mode and median. 10, 13, 15, 16, 17, 17, 20 The mode (the modal average ) 17? 16 ? The median 10 + 13 + 15 + 16 + 17 + 17 + 20 7 The mean ? = 15.43
Averages Round 2! Copy these numbers down, and work out the mean, mode and median. 13, 13, 17, 20 The mode (the modal average ) 13 ? When there s two items in the middle, we use the value in between: i.e. add them and divide by 2. 15 ? The median 15.75 ? The mean The range is the difference between the smallest and largest number. 7 ? The range
Puzzles involving the mean In pairs, see how many of these puzzles you can work out 1 The mean average of Dr Frost and Sebastian s age is 19.5. If Sebastian is 13, how old is Dr Frost? 2 If the range of two numbers is 6 and the their mean is 15, what are the two numbers? ? Answer: 12 and 18 Answer: 26 ? The mean of the four numbers is 8. What is the missing number? The mode of four numbers is 5. The median is 6.5 and the mean is 7. What is the range? 3 4 3 4 5 ? Answer: 7 (The numbers are 5, 5, 6, 12) ? Answer: 20 ?
Exercises Worksheet provided!
KS3 Mean of Frequency Tables Dr J Frost (jfrost@tiffin.kingston.sch.uk) Last modified: 22nd November 2013
Mean of Frequency Tables Age of Dog 10 11 12 13 14 Frequency 3 4 7 6 1 Bro Tip: Imagine if we actually listed out the values how would we find the mean? The frequency tells us how frequent the age of 10 is, i.e. how many times it appears. ???? = 10 3 + 11 4 + 12 7 + 13 6 + 14 1 21 = 11.9 ?
Your Go... Cost 1.50 1.65 1.70 1.80 2.00 Frequency 1 20 21 5 2 Mean cost of beefburger horseburger: = = 1.70 83.20 49 ? Weight 2kg 3kg 4kg 5kg 6kg Frequency 4 0 8 7 3 Mean weight of cats: = = 4.23kg 93 22 ?
Mean of Grouped Data A number of members of 8IW are running in a race. Their times were as follows Time (secs) Frequency 35 ? < 40 6 40 ? < 50 12 50 ? < 70 9 ??.? ? + ?? ?? + ?? ? ?? = ??.?? ?? ??? Estimate of mean: ? Because we don t know the exact times within each group. ? Why is it an estimate?
Test Your Understanding Weight of horse (kg) Frequency 80 w < 100 46 100 w < 150 80 150 ? < 200 103 Age of rock (years) Frequency ???????? ?? ???? =32165 = 140.5?? ? 0 a < 100 40 229 100 a < 400 24 400 a < 1000 5 ???????? ?? ???? =11500 = 166.7 ????? ? 69
Exercises (Provided on printed sheet) 4 Sam collects the weights of 15 squirrels and puts them into weight ranges. His data is presented below. Estimate the mean weight of a squirrel. At a party, thirty people have an age of 30, forty have an age of 40 and fifty an age of fifty. What is their average age? ??.? ? 1 Weight Frequency 10-16kg 7 16-20kg 3 20-30kg 4 30kg-32kg 1 ??.??? ? In a hardware shop, there are 30 spanners costing 6, 55 hacksaws costing 9 and 10 soldering irons costings 20. What is the average cost per item? ?.?? ? 2 Miss Clarke values a number of pieces of artwork in the Tiffin School Vault. The price ranges are summarised below. Estimate the average value of a piece of art in school. 5 Value Frequency 0- 1000 10 1 000-5 000 25 5 000- 20 000 6 20 000- 100 000 1 3 Using this frequency table, find the average height of a turnip. 5119.05 ? Height (nearest cm) Frequency 6cm 3 7cm 8 8cm 12 9cm 4 10cm 1 I record the times of 50 runners in a 10km race. Their times are summarised below. Determine their mean time in minutes. 6 ?.???? ? Time (minutes) Frequency 35-40 5 40-42 15 42-48 20 48-60 10 44.85 minutes ?
Exercises I visit the lost island of Laurie and collect the weights of Kenneybirds. There are 5 birds with a weight of 10?? to ? ?? and 5 birds with a weight between ? ?? and 20??. The estimate of the mean is 14??. Determine ?. 6 ?? + ? ? ? + ?? ? ? ? + ? = ?? ?? ? = ?? ?? I travel back in time and collect the heights of a number of Damonsaurus. There are ? dinosaurs with a height between 5- 7km and 4 dinosaurs with heights between 7-11km. The estimate of the mean height is 6.2??. How many Damonsaurus are there in total? 7 ?? + ?? ? + ? = ?.? ? ? = ?? ??