Understanding Interacting Fields and Feynman Diagrams in Quantum Field Theory
Delve into the fascinating world of quantum field theory with a focus on interacting fields and Feynman diagrams. Explore perturbation theory, correlation functions, Wick's theorem, and Feynman diagram rules to gain insights into preserving causality, calculating two-point correlation functions, and generalizing to multiple fields. Unravel the complexities of field interactions through detailed analyses and visual representations.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
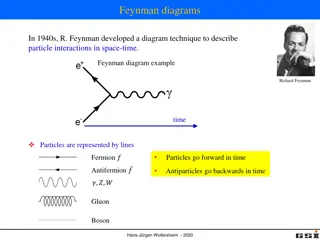
Review of Interacting Felds and Feynman Digrams Spesker: Lei-wang
Why do I want to show this to you?
Contents PART 01 Perturbation Theory PART 02 Correlation Functions PART 03 Wick's Theorem PART 04 Feynman Diagrams
Perturbation Theory to preserve causality: interactions:
Perturbation Theory phi-fourth throry QED yukawa theory g scalar field g i 5 pesudoscal ar field renormalizable 4 L =
Correlation Functions two-point correlation function Feynman propagator we would like to know how this expression changes in the interacting interacting theory?
Correlation Functions where
Correlation Functions properties
Correlation Functions where our final result:
Wick's Theorem where normal ordering symbol N relation between T and N
Wick's Theorem generalization to arbitrarily many fields example prove Wick's theorem
Feynman Diagrams with the exponential expanded the second term
Feynman Diagrams final result position-space Feynman rules
Feynman Diagrams momentum-space Feynman rules
Feynman Diagrams Consider T disconnected pieces
Feynman Diagrams sum of all diagrams for connected pieces then we get
Feynman Diagrams denominator finally generalization example