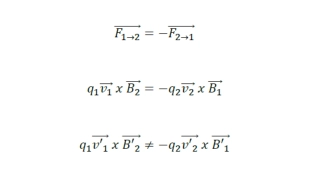Understanding Frames of Reference and Relativity

Slide Note

Explore the concept of frames of reference in physics, distinguishing between inertial and non-inertial frames. Learn about the laws of Newtonian mechanics, guidelines for inertial frames of reference, and delve into the intriguing realm of the Special Theory of Relativity with engaging visual aids and thought experiments.

seco_rie Follow

Uploaded on Sep 13, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

E N D

Presentation Transcript

11.1 Frames of Reference and Relativity

Inertial Frame of Reference (IFOR) a frame of reference in which the law of inertia holds The FOR must be at a constant velocity (not speed) or at rest In both, net force = 0N

a) Pick-up at const vel b) Earth is stationary

Non-Inertial Frame of Reference (NIFOR) a frame of reference that does not obey the law of inertia the reference involves acceleration. (A Nonzero Net Force)

From inside the accelerating car, the ball appears to move without a force acting on it (Breaks Newt s 2ndLaw)

Guidelines for IFORs 1. An inertial frame of reference is one which an object has no net force acting on it; and it is at rest or moving at a constant velocity.

Guidelines for IFORs 2. The laws of Newtonian mechanics are only valid in an inertial frame of reference.

Guidelines for IFORs 3. The laws of Newtonian mechanics apply equally in all inertial frames of reference.

In an IFOR, you cannot tell if you are moving or not Your FOR could be moving at a constant vel. and you would never know

Special Theory of Relativity What would happen if you are moving at the speed of light in a car and then you turn your headlights on? This is the type of thought experiment Einstein performed to conceptualize movement at very high speeds (closer to speed of light)

Special Theory of Relativity 1. The relativity principle: all the laws of physics are valid in all inertial frames of reference.

Special Theory of Relativity 2. The consistency of the speed of light: light travels through empty space with a speed of c = 3.00 X 108 m/s relative to all inertial frames of reference. Einstein defined light as the universal speed limit

Simultaneity The occurrence of two or more events at the same time is a relative concept Two events that are simultaneous in one FOR are in general not simultaneous in a second FOR moving with respect to the first Simultaneity is not an absolute concept

11.2 Relativity of Time, Length and Momentum

Time dilation: the effect of time occurring slower in one system compared to another system. Note: As objects move faster relative to the Earth, time slows down.

Note: Dilation means widening, thus time dilation means widening time. Proper time occurs when an observer remains in one system of time.

Einsteins Proof for Time Dilation The light clock

tm= ts/[1-(v2/c2)]0.5 where tm= time for moving observer ts= time for stationary observer v = speed of moving observer ( in m/s) c = speed of light ( 3.00 X 108m/s)

Note: Use the person in the ship as a reference. Example # 1: A person travels for 3.0 years at the speed 0.70c relative to a physics student on Earth. Calculate the time that has passed for the student.

Solution tm= ts/[(1-(v2/c2)]0.5 tm= (3.0 years)/[1- (0.70c)2/c2] 0.5 = 4.2 years The time for the moving observer is 4.2 years.

The Twin Paradox Einstein had a thought experiment involving two twins, in which one went to a star at a speed near the speed of light and then came back to Earth.

Which twin would be older?

The one on Earth?

Or the one on the spacecraft?

Proper Length: the length of an object at rest Length Contraction: the shortening of distances in a system as seen by an observer in motion relative to that system.

Length contraction only occurs in the direction of motion

Lm= Ls(1- v2/c2)0.5 Where Lm= length for moving observer Ls= length for stationary observer v = speed of moving observer ( in m/s) c = speed of light ( 3.00 X 108m/s)

Example # 2: Calculate the proper length of an object that has a Lm= 45 m when it is moving at 0.60c.

Solution Lm= Ls(1- v2/c2)0.5 Ls= Lm/(1- v2/c2)0.5 = (45 m) /[1- (0.60c)2/c2]0.5 = 56 m The proper length is 56 m.

Example # 3 If two spaceships, 40m long, are travelling towards each other at 0.20c and 0.30c, what will each pilot see as the length of the other ship?

Relativistic Momentum: the momentum of an object travelling at a speed at 0.10c or greater.

p = mv/(1- v2/c2)0.5 where p = magnitude of relativistic momentum (in kg m/s) m = rest mass (in kg) v = speed of an object (in m/s)

Example # 3: Calculate the magnitude of relativistic momentum of an object that has a mass of 600 kg at a speed of 0.80c.

Solution p = mv/(1- v2/c2)0.5 p = (600kg)(0.80)(3.00X108ms) [1-(0.80c)2/c2]0.5 p = 2.4 X 1011kg m/s The magnitude of relativistic momentum is 2.4 X 1011kg m/s.