Understanding Educational Statistics: Key Concepts and Calculations

Statistics is the science of collecting, describing, and interpreting data. It involves two main areas - Descriptive Statistics for organizing and presenting data and Inferential Statistics for drawing conclusions about populations. An example scenario demonstrates the terms like population, sample, variable, data, experiment, parameter, and statistic. The process of calculating mean and median with detailed illustrations is also covered in the content.

• Educational Statistics
• Data Collection
• Descriptive Statistics
• Inferential Statistics

honey Follow

Uploaded on Aug 03, 2024 | 1 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Educational statistics

2. 1.1: What is Statistics? Statistics: The science of collecting, describing, and interpreting data. Two areas of statistics: Descriptive Statistics: collection, presentation, and description of sample data. Inferential Statistics: making decisions and drawing conclusions about populations.

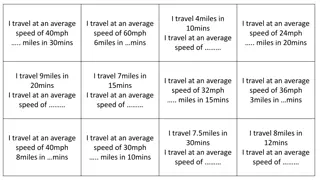
3. Example: A college principal is interested in learning about the average age of faculty. Identify the basic terms in this situation. The population is the age of all faculty members at the college. A sample is any subset of that population. For example, we might select 10 faculty members and determine their age. The variable is the age of each faculty member. One data would be the age of a specific faculty member. The data would be the set of values in the sample. The experiment would be the method used to select the ages forming the sample and determining the actual age of each faculty member in the sample. The parameter of interest is the average age of all faculty at the college. The statistic is the average age for all faculty in the sample.

4. Calculation of Mean (long method) Class Interval (CI) Mid-Point (X) Frequency (f) 2 3 2 6 8 8 7 5 9 N=50 Frequency x Midpoint (f x X) 45-49 40-44 35-39 30-34 25-29 20-24 15-19 10-14 5-9

5. Calculation of Mean (long method) Class Interval (CI) Mid-Point (X) 47 42 37 32 27 22 17 12 7 Frequency (f) 2 3 2 6 8 8 7 5 9 N=50 Frequency x Midpoint (f x X) 94 126 74 192 216 176 119 60 63 fX=1120 45-49 40-44 35-39 30-34 25-29 20-24 15-19 10-14 5-9

6. Substituting the values in the formula: Mean = fX N Or Mean = 1120 = 22.40 50

7. Calculation of Median Class Interval (CI) Exact-Limits Frequency (f) Cumulative Frequency (Cumf) MedianliesCI=N / 45-49 40-44 35-39 30-34 25-29 20-24 15-19 10-14 5-9 2 3 2 6 8 8 7 5 9 N=50

8. Calculation of Median Class Interval (CI) Exact-Limits Frequency (f) Cumulative Frequency (Cumf) 50 48 45 43 37 29 21 14 9 45-49 40-44 35-39 30-34 25-29 20-24 15-19 10-14 5-9 44.5-49.5 39.5-44.5 34.5-39.5 29.5-34.5 24.5-29.5 19.5-24.5 14.5-19.5 9.5-14.5 4.5-9.5 2 3 2 6 8 8 7 5 9 N=50

9. Substituting the values in the formula: Median = L + [N/2 Cumfb] x i L = exact lower limit of the C I in which the median lies (19.5) Cumfb= cumulative frequency below the C I containing Median (21) fw = frequency within the C I containing the Median (8) i = size of the C I (5) fw

10. Median = 19.5 + [ 50/2 21 ] x 5 = 19.5 + [ 25 21 ] x 5 = 19.5 + 4 x 5 8 = 19.5 + 2.5 = 22 8 8

11. Mode The Mode refers to the number that occurs the most frequently. It s easy to remember the first two numbers are the same! MOde and MOst Frequently!

12. Calculation of mode Mode = 3 Median - 2 Mean from the distribution given above : Median = 22 and Mean = 22.40 Substituting the values given above Mode = 3 x 22 2 x 22.40 = 21.2

13. Calculation of Mode Class Interval (CI) Exact limits Frequency (f) 2 3 2 6 8 8 7 5 9 N=50 45-49 40-44 35-39 30-34 25-29 20-24 15-19 10-14 5-9 44.5-49.5 39.5-44.5 34.5-39.9 29.5-34.5 24.5-29.5 19.5-24.5 14.5-19.5 9.5-14.5 4.5-9.5

14. Mode = L + (f-fb) + (f-fa) L= exact lower limit of modal class interval f= frequency of the modal class interval fb= frequency below the modal class interval fa= frequency above the modal class interval i= size of the class interval L = 25, f = 8, fb= 8, i = 5, fa = 6 Mode = 24.5 + 8 8 x 5 (8-8) + (8-6) = 21.5 f fb x i

15. Measures of variability Average deviation Standard deviation Quartile deviation

16. Average deviation The average deviation is the average distance between the mean and scores in the distributions

17. Calculate average deviation from grouped data Class interval Mid-Point X Frequency f fX X-M |X-M| f|X-M| 50-59 2 40-49 4 30-39 12 20-29 15 10-19 10 0-9 7 N=50

18. Calculate average deviation from grouped data Class interval Mid-Point X Frequency f fX X-M |X- M| f|X-M| 50-59 54.5 2 109 +29.6 29.6 59.2 40-49 44.5 4 178 +19.6 19,6 78.4 30-39 34.5 12 414 +9.6 9.6 115.2 20-29 24.5 15 367.5 0.4 0.4 6.0 10-19 14.5 10 145 -10.4 10.4 104.0 0-9 4.5 7 31.5 -20.4 20.4 142.8 fX=1245 f|X- M|=505.6 N=50

19. Mean = fX N Mean = 1245 Average Deviation= f|X-M| = 505.6 =10.11 = 24.9 50 N 50

20. Standard Deviation Standard Deviation shows the variation in data. If the data is close together, the standard deviation will be small. If the data is spread out, the standard deviation will be large. Standard Deviation is often denoted by the lowercase Greek letter sigma, .

21. Calculation of Standard Deviation (real mean method) Class Interval (CI) Mid- Point (X) Frequency (f) Frequency x Midpoint (f x X) Deviation of X from mean X-M f(X-M) f(X-M) 45-49 2 40-44 3 35-39 2 30-34 6 25-29 8 20-24 8 15-19 7 10-14 5 5-9 9 N=50

22. Calculation of Standard Deviation (real mean method) Class Interval (CI) Mid- Point (X) Frequency (f) Frequency x Midpoint (f x X) Deviation of X from mean X-M 24.6 f(X-M) f(X-M) 45-49 47 2 94 49.2 1210.32 40-44 42 3 126 19.6 58.8 1152.48 35-39 37 2 74 14.6 29.2 426.23 30-34 32 6 192 9.6 57.6 552.96 25-29 27 8 216 4.6 36.8 169.28 20-24 22 8 176 -0.4 -3.2 1.28 15-19 17 7 119 -5.4 -37.8 204.12 10-14 12 5 60 -10.4 -52.0 540.8 5-9 7 9 63 -15.4 -138.6 2134.4 fX=1120 f(X-M) =6392 N=50

23. Using the formula Mean = fX = 1120 N 50 Standard deviation( ) = f(X-M) N = 6392 50 = 127.84 = 11.31 = 22.40

24. Quartile deviation The semi-inter quartile range which is also known as quartile deviation can be defined as a half of the difference between the 75th percentile and the 25th percentile Q = Q - Q OR P - P 2 2

25. Calculation of Quartile Deviation Class Interval (CI) Limits Exact- Frequency (f) Cumulative Frequency (Cumf) 45-49 2 40-44 3 35-39 2 30-34 6 25-29 8 20-24 8 15-19 7 10-14 5 5-9 9 N=50

26. Calculation of Quartile Deviation 50 x 75 = 37.5 100 Class Interval (CI) Exact- Limits Frequency (f) Cumulative Frequency (Cumf) Q lies in this C I 45-49 44.5-49.5 2 50 40-44 39.5-44.5 3 48 35-39 34.5-39.5 2 45 30-34 29.5-34.5 6 43 Q lies in this C I 25-29 24.5-29.5 8 37 20-24 19.5-24.5 8 29 15-19 14.5-19.5 7 21 10-14 9.5-14.5 5 14 50 x 25 =12.5 100 5-9 4.5-9.5 9 9 N=50

27. Substituting the values in the formula Q = L + (N/4 Cumfb) x i fq Q = L + (3N/4 Cumfb) x i fq L= the exact lower limit of the interval in which the quartile falls i = size of the class interval Cumfb = cumulative frequency below the C I which contains the quartile Fq = the frequency in the C I containing quartile

28. Calculation of Q Q = L + (N/4 Cumfb) x i fq L = 9.5, Cumfb=9, fq=5, i=5, N=50 Q = 9.5 + (50/4 9) x 5 5 Q = 9.5 + 3.5 = 13.0

29. Calculation of Q Q = L + (3N/4 Cumfb) x i fq L = 29.5, Cumfb=37, fq=6, i=5, N=50 Q = 29.5 + (3x50/4 37) x 5 6 Q = 29.5 + 0.42 = 29.92

30. Calculation of Q Q = Q - Q 2 Q = 29.92 13.00 = 16.92 = 8.46 2 2

31. Coefficient of correlation A Coefficient of correlation is a single number that tells us to what extent two variables or things are related and to what extent variations in one variable go with variations in the other

32. Karl Pearsons Product Moment Correlation (r) Deviation score method X-M x (X-M ) x (X-M )x(X- My) xy 20 X Y X-My y (X-My) y 10 11 4 5 16 25 8 7 2 1 4 1 2 6 2 0 -4 0 16 0 4 6 -2 0 4 0 0 2 4 -4 -2 16 4 8 =30 =30 x =40 y =46 xy=30 Mean X = 30/5 = 6 Mean Y = 30/5 = 6

33. Formula: Coefficient of correlation (r) r = xy x y r = 30 (40)(46) r = 30 42.9 6.54 = 30 = 0.7

34. Rank Difference Coefficient of correlation Students Score on test 1 (X) Score on test 2 (Y) rank on test 1 (R ) Rank on test 2 (R ) Difference between ranks (D) 1.0 -2.5 3.5 0 -1.0 -0.5 -1.0 -1.0 1.0 0.5 Difference squared (D ) 1.00 6.25 12.25 0 1.00 0.25 1.00 1.00 1.00 0.25 D =24.00 A B C D E F G H I J 10 15 11 14 16 20 10 8 7 9 16 16 24 18 22 24 14 10 12 14 6.5 3 5 4 2 1 6.5 9 10 8 5.5 5.5 1.5 4 3 1.5 7.5 10 9 7.5 N=10

35. Formula: rho = 1 - 6 D N(N - 1) rho = 1 - 6 x 24 10(10 - 1) rho = 1 - 10 x 99 rho = 1 - 144 990 rho = 1 - 990 144 990 144 = 0.855