Understanding B+ Tree Data Structure
Explore the B+ tree data structure, its rules, insertion and deletion operations, node structure, and variations like the B-tree. Learn about maintaining balance, node sizes, and pointers in this efficient data structure designed for disk-based storage systems.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
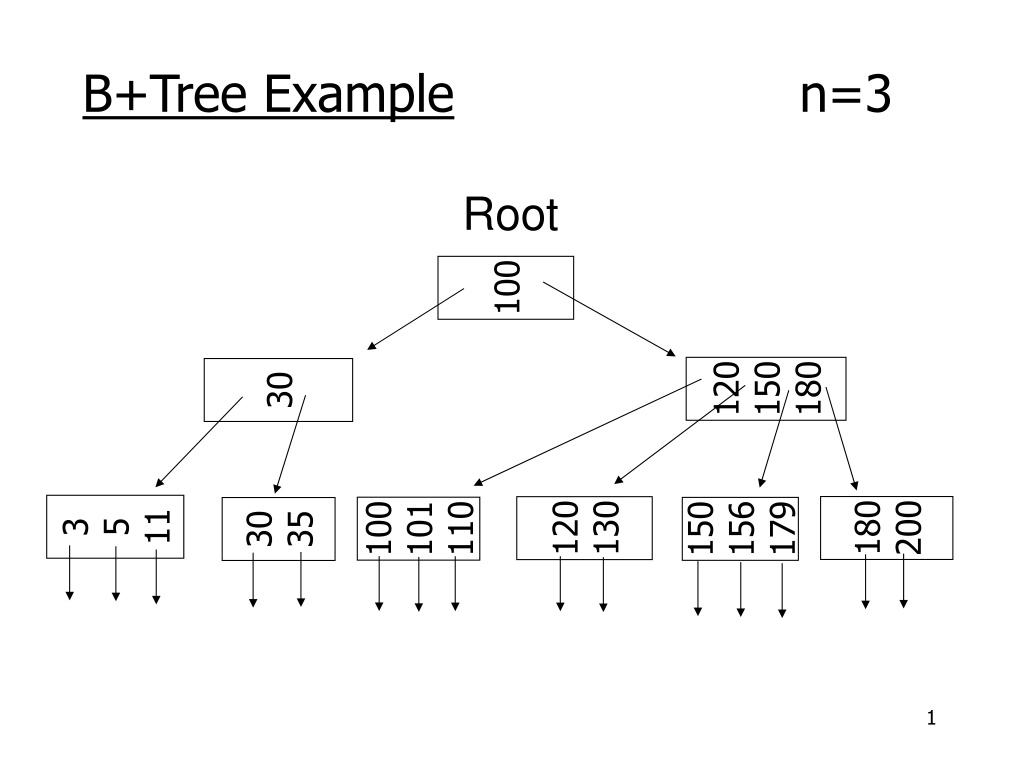
B+Tree Example n=3 Root 100 120 150 180 30 180 200 120 130 100 101 110 156 150 179 11 35 30 3 5 1
B+ tree in textbooks notation n=3 Leaf: 30 35 30 35 Non-leaf: 30 30 2
Size of nodes: n+1 pointers n keys (fixed) 3
Dont want nodes to be too empty Use at least (n+1)/2 pointers Non-leaf: (n+1)/2 pointers to data Leaf: 4
B+tree rules tree of order n (1) All leaves at same lowest level (balanced tree) (2) Pointers in leaves point to records except for sequence pointer (to next leaf) 5
(3) Number of pointers/keys for B+tree Max Max Min Min ptrs keys ptrs data keys Non-leaf (non-root) Leaf (non-root) Root (n+1)/2 (n+1)/2 - 1 n+1 n (n+1)/2 (n+1)/2 n+1 n n+1 n 1 1 6
Insert into B+tree (a) simple case (insert 32) space available in leaf (b) leaf overflow (insert 7) (c) non-leaf overflow (insert 160) (d) new root (insert 45) 7
Deletion from B+tree (a) Simple case - no example (b) Coalesce with neighbor (delete 50) (c) Re-distribute keys (delete 50) (d) Cases (b) or (c) at non-leaf (delete 37) 8
B+tree deletions in practice Often, coalescing is not implemented Too hard and not worth it! 9
Variation on B+tree: B-tree (no +) Idea: Avoid duplicate keys (leaf and non-leaf) Have record pointers in non-leaf nodes 10
K1 P1 K2 P2 K3 P3 to record with K1 to record with K2 to record with K3 to keys < K1 to keys K1<x<K2 to keys K2<x<k3 to keys >k3 11
B-tree example n=2 125 65 105 145 165 25 45 85 110 160 100 120 130 140 150 170 180 20 10 30 40 50 60 70 80 90 12
B-tree example sequence pointers not useful now! (but keep space for simplicity) n=2 125 65 105 145 165 25 45 85 110 160 100 120 130 140 150 170 180 20 10 30 40 50 60 70 80 90 13
Note on inserts Say we insert record with key = 25 n=3 leaf 30 10 20 14
Note on inserts Say we insert record with key = 25 n=3 leaf 30 10 20 Afterwards: 20 10 25 30 15