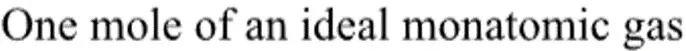Thermodynamic Processes

The concepts of internal energy, enthalpy, and entropy through a breakdown of a thermodynamic problem involving different paths and states. Gain insights into reversible and irreversible processes, state functions, and path independence. Discover the calculations and relationships between temperature, pressure, volume, and work in various thermodynamic scenarios.

• Thermodynamics
• Processes
• Internal Energy
• Enthalpy
• Entropy

cabsh Follow

Uploaded on Mar 06, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Calculation Session 6: Exercise 6 Kaleigh Soucy ( 23) Donovan Cho ( 25) Vivian Liu ( 26) Professor Molenium @ STP Professor Molenium @ 0.5 atm

2. Fun Fact: You can purchase a Professor Molenium keychain from the American Chemical Society website.

3. Problem Breakdown! Initial Ti = 298 K Pi = 10 atm Final Tf = 253.2 K Pf = 2 atm Pext = 2 atm

4. Given i U? H? S? f Are U, H, and S path functions or state functions? State Functions! Path Independent Does the path matter? Reversible for S

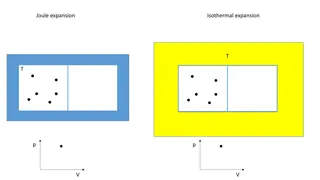
5. Path Options Lecture T4 Isobaric, P = 0 Not always reversible! state 1 state 4 P1 Isothermal, = 0 1 = ( ) P nRT for an ideal gas: V Adiabatic (q = 0) Isochoric V = 0 state 2 P2 state 3 0 0 V1 V2

6. U? Initial 1: Isotherm Path 1: Isothermal Isothermal paths are convenient! ? = ???? ?1 2 = 0 Path 2: Isochoric Makes sense for Cv ? = ???? ?2 3 = 3 0 Final 2: IsoP OR 2: IsoV 2??(?3 ?2)

7. U? 1: IsoT 2: IsoV ?2 3 = 3 2??(?3 ?2) ?2 3 = 3 Utotal = ?1 2+ ?2 3 = 0 559 J = -559 J 2(1.0 mol)(8.314 J/mol K)(253.2 298 K) = -559 J

8. H? Initial 1: Isotherm Path 1: Isothermal Isothermal paths are convenient! ? = ???? ?1 4 = 0 Path 2: Isobaric Makes sense for Cp ? = ???? ?4 3 = 5 Final 0 2: IsoP OR 2: IsoV 2??(?3 ?4)

9. H? Initial 1: Isotherm ?4 3 = 5 2??(?3 ?2) Final 2: IsoP ?4 3 = 5 Htotal = ?1 4+ ?4 3 = 0 931 J = -931 J 2(1.0 mol)(8.314 J/mol K)(253.2 298 K) = -931 J ? = ? + ?? also works!

10. S? Initial 1: Isotherm 1: dS = ???? ? Final U =q + w = 0 q = -w = PdV P = ??? ?? ??? ? dS = S14 = -(1.0 mol)(8.314 J/mol K) ln(2 ??? = 13.38 J/mol 10 ???) ?? ??) = -nR ln( ?? ??) S = nR ln(

11. S? Initial 1: Isotherm 2: At constant pressure, H = q S = ?? ??) = 5 S43 = 5 ???? ? Final 2: IsoP ?? ??) S = Cp ln( 2 nR ln( 2(1.0 mol)(8.314 J/mol K) ln(253.2 ? 298 ?) = -3.39 J/mol Stotal = S14+ S43 = 9.99 J/mol

12. Key Takeaways! U, H, S are state functions! There are no wrong paths only inefficient ones Understand reversible vs. irreversible processes U = H = 0 for isothermal processes (ideal gas) H = q at constant pressure For an ideal monatomic gas: Cv = 3 Cp = 5 2nR 2nR