Solving Simultaneous Equations Using Bar Method
Simultaneous Equations
LO: to be able to represent and solve
simultaneous equations using the Bar
Method.
Using the bar method, solve
4x + y = 17
2x + y = 11
Draw a bar for each
equation
Compare the bars to try and
eliminate either x or y
Using the bar method, solve
4x + y = 17
2x + y = 11
The second bar matches
part of the first bar
11
Using the bar method, solve
4x + y = 17
2x + y = 11
Subtract it to find
the value of x
6
11
2x = 6
So x = 3
17 –
11
= 6
4x + y -
(2x + y)
= 2x
x = 3
Using the bar method, solve
4x + y = 17
2x + y = 11
Substitute the value
of x into one of the
original bars to find y
Subtract to find y
3
+ 3
= 6
6
y = 11 – 6
y = 5
x = 3
y = 5
Now try these. Using the bar method, solve:
1) 5x + 2y = 13
x + 2y = 9
2)
x + 3y = 9
x + y = 6
Challenge:
3) 2x + 3y = 19
6x + 2y = 22
Answers
1)
x = 1
y = 4
2)
x = 4.5
y = 1.5
3)
x = 2
y = 5
Using the bar method, solve
2x + y = 7
5x - y = 14
The y is subtracted from the
second bar to get 14
14
x
x
x
Combine the bars by
adding to eliminate y
Using the bar method, solve
2x + y = 7
5x - y = 14
The y is subtracted from the
second bar to get 14
14
x
x
x
Combine the bars by
adding to eliminate y
Using the bar method, solve
2x + y = 7
5x - y = 14
The y is subtracted from the
second bar to get 14
x
x
x
7 + 14 = 21
Combine the bars by
adding to eliminate y
2x + 5x + y
- y
= 7x
7x = 21
So
x = 3
x = 3
Using the bar method, solve
2x + y = 7
5x - y = 14
Substitute the value of x into
one of the original bars to
find y
x
x
x
7 + 14 = 21
Combine the bars by
adding to eliminate y
3 3
1
x = 3
3 + 3 = 6
7 – 6 = 1
So y = 1
y = 1
Learn how to represent and solve simultaneous equations using the Bar Method. Step-by-step illustrations show how to eliminate variables and find solutions. Practice with provided examples and a challenge problem to enhance your understanding.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Simultaneous Equations LO: to be able to represent and solve simultaneous equations using the Bar Method.
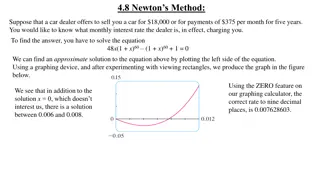
Using the bar method, solve 4x + y = 17 2x + y = 11 Draw a bar for each equation 17 y x x x x Compare the bars to try and eliminate either x or y 11 x x y
Using the bar method, solve 4x + y = 17 2x + y = 11 The second bar matches part of the first bar 17 y x x x x 11 11 x x x x y y
Using the bar method, solve 4x + y = 17 2x + y = 11 x = 3 Subtract it to find the value of x 17 y x x x x x x 4x + y - (2x + y) = 2x 17 11 = 6 x x y 11 6 2x = 6 So x = 3
Using the bar method, solve 4x + y = 17 2x + y = 11 x = 3 Substitute the value of x into one of the original bars to find y y = 5 17 y x x x x Subtract to find y 6 11 x x 3 = 6 y y = 11 6 y = 5 + 3
Now try these. Using the bar method, solve: 1) 5x + 2y = 13 x + 2y = 9 Answers 1) x = 1 y = 4 2) x + 3y = 9 x + y = 6 Challenge: 3) 2x + 3y = 19 6x + 2y = 22 2) x = 4.5 y = 1.5 3) x = 2 y = 5
Using the bar method, solve 2x + y = 7 5x - y = 14 The y is subtracted from the second bar to get 14 7 x x y x x x x x y 14 Combine the bars by adding to eliminate y
Using the bar method, solve 2x + y = 7 5x - y = 14 The y is subtracted from the second bar to get 14 11 x x x x y y x x x x x y 14 Combine the bars by adding to eliminate y
Using the bar method, solve 2x + y = 7 5x - y = 14 x = 3 The y is subtracted from the second bar to get 14 7 x x y 2x + 5x + y - y = 7x x x x x x x x y y 7 + 14 = 21 7x = 21 So x = 3 Combine the bars by adding to eliminate y
Using the bar method, solve 2x + y = 7 5x - y = 14 x = 3 y = 1 Substitute the value of x into one of the original bars to find y 3 + 3 = 6 7 6 = 1 So y = 1 3 3 1 7 x x y x x x x x x x y y 7 + 14 = 21 Combine the bars by adding to eliminate y
