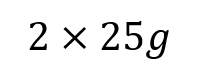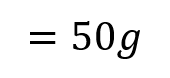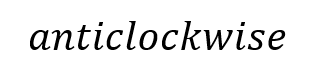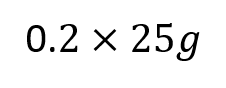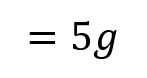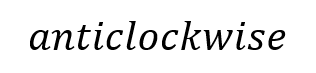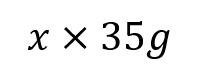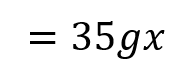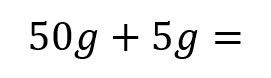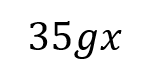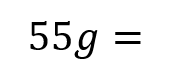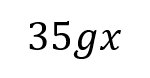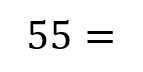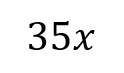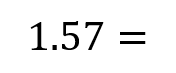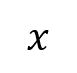Solving Problems with Centre of Mass
You can solve problems about non-uniform
bodies by finding or using the centre of
mass
The mass of a non-uniform body can be
modelled as acting at its centre of mass
This means the weight of the rod may
not necessarily be in the centre as it has
been so far
Sam and Tamsin are sitting on a non-uniform
plank AB of mass 25kg and length 4m.
The plank is pivoted at M, the midpoint of
AB, and the centre of mass is at C where AC
= 1.8m.
Tamsin has mass 25kg and sits at A. Sam
has mass 35kg. How far should Sam sit from
A to balance the plank?
A
B
25g
25g
35g
C
M
R
M
Let Sam sit ‘x’ m from the midpoint
Take moments about M (this way we don’t need to know R
M
)
1.8m
0.2m
x
(1)
(2)
(3)
(1)
(2)
(3)
The rod is in equilibrium so anticlockwise = clockwise
Group terms
Divide by g
Divide by 35
Sam should sit 3.57m from A (or 0.43m from B)
Make sure you always read where the distance should be measured from!
Moments
4D
You can solve problems about non-
uniform bodies by finding or using the
centre of mass
A rod AB is 3m long and has weight 20N.
It is in a horizontal position resting on
supports at points C and D, where AC =
1m and AD = 2.5m.
The magnitude of the reaction at C is
three times the magnitude of the
reaction at D.
Find the distance of the centre of mass
of the rod from A.
C
D
1m
1.5m
0.5m
R
C
R
D
A
B
20N
R
C
= 3R
D
Estimate where the centre of mass is on your diagram
We can replace RC with 3R
D
Now find the normal reactions
3R
D
5N
15N
Divide by 4
Moments
4D
Calculate
You can solve problems about non-
uniform bodies by finding or using the
centre of mass
A rod AB is 3m long and has weight 20N.
It is in a horizontal position resting on
supports at points C and D, where AC =
1m and AD = 2.5m.
The magnitude of the reaction at C is
three times the magnitude of the
reaction at D.
Find the distance of the centre of mass
of the rod from A.
C
D
1m
1.5m
0.5m
B
20N
5N
15N
Now take moments about A, calling the required distance ‘x’
(You’ll find it is usually easiest to do this from the end of the rod!)
(1)
(3)
(2)
x
(1)
(2)
(3)
Equilibrium so anticlockwise = clockwise
Group terms
Calculate
The centre of mass is 1.38m from A
A
Moments
4D
Learn how to apply the concept of centre of mass to solve problems involving non-uniform bodies in equilibrium. Discover methods to find the centre of mass and calculate distances for achieving balance in various scenarios.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Teachings for Exercise 4D
Moments RM You can solve problems about non-uniform bodies by finding or using the centre of mass 1.8m 0.2m x A B C M The mass of a non-uniform body can be modelled as acting at its centre of mass (1) (2) (3) 25g 25g 35g Let Sam sit x m from the midpoint Take moments about M (this way we don t need to know RM) (1) 2 25? = 50? ????????????? This means the weight of the rod may not necessarily be in the centre as it has been so far (2) Sam and Tamsin are sitting on a non-uniform plank AB of mass 25kg and length 4m. 0.2 25? = 5? ????????????? (3) ? 35? = 35?? ????????? The plank is pivoted at M, the midpoint of AB, and the centre of mass is at C where AC = 1.8m. The rod is in equilibrium so anticlockwise = clockwise 50? + 5? = 35?? Group terms Divide by g Divide by 35 55? = 35?? Tamsin has mass 25kg and sits at A. Sam has mass 35kg. How far should Sam sit from A to balance the plank? 55 = 35? 1.57 = ? Sam should sit 3.57m from A (or 0.43m from B) Make sure you always read where the distance should be measured from! 4D
Moments RC = 3RD 15N 3RD RC RD 5N You can solve problems about non- uniform bodies by finding or using the centre of mass 1m 1.5m 0.5m A B C D A rod AB is 3m long and has weight 20N. It is in a horizontal position resting on supports at points C and D, where AC = 1m and AD = 2.5m. 20N Estimate where the centre of mass is on your diagram We can replace RC with 3RD Now find the normal reactions The magnitude of the reaction at C is three times the magnitude of the reaction at D. 4??= 20 Divide by 4 ??= 5 Calculate ??= 15 Find the distance of the centre of mass of the rod from A. 4D
Moments (1) (3) 15N 5N You can solve problems about non- uniform bodies by finding or using the centre of mass 1m 1.5m 0.5mB A x C D A rod AB is 3m long and has weight 20N. It is in a horizontal position resting on supports at points C and D, where AC = 1m and AD = 2.5m. (2) 20N Now take moments about A, calling the required distance x (You ll find it is usually easiest to do this from the end of the rod!) (1) (2) (3) 2.5 5 = 12.5 ?? ????????????? 1 15 = 15 ?? ????????????? The magnitude of the reaction at C is three times the magnitude of the reaction at D. ? 20 = 20? ?? ????????? Equilibrium so anticlockwise = clockwise Find the distance of the centre of mass of the rod from A. 15 + 12.5 = 20? Group terms 27.5 = 20? Calculate 1.38 = ? The centre of mass is 1.38m from A 4D
