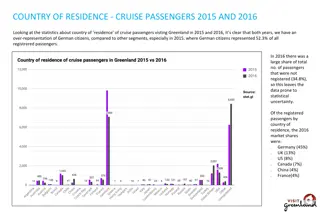
Regression Model for Predicting Crew Size of Cruise Ships

A regression model was built to predict the number of crew members on cruise ships using potential predictor variables such as Age, Tonnage, Passenger Density, Cabins, and Length. The model showed high correlations among predictors, with Passengers and Cabins being particularly problematic. The full model with 5 predictors and 6 parameters yielded an R-Square of 0.9195. Backward elimination based on AIC was also conducted to refine the model.

• Regression model
• Cruise ships
• Predictor variables
• Correlation plot
• Backward elimination

legionle Follow

Uploaded on Sep 17, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

Presentation Transcript

1. Regression Model Building Predicting Number of Crew Members of Cruise Ships

2. Data Description n=158 Cruise Ships Dependent Variable Crew Size (100s) Potential Predictor Variables Age (2013 Year Built) Tonnage (1000s of Tons) Passengers (100s) Length (100s of feet) Cabins (100s) Passenger Density (Passengers/Space)

3. Correlation Plot / Matrix High correlations among the predictors. (Passengers and Cabins is very problematic) Passengers/Cabins: r=.976 Tonnage / Cabins: r=.949 Tonnage / Passengers: r=.945 Consider model with Predictors: Age, Tonnage, Passdens, Cabins, Length

4. Data First 20 Cases Ship Journey Quest Celebration Conquest Destiny Ecstasy Elation Fantasy Fascination Freedom Glory Holiday Imagination Inspiration Legend Liberty* Miracle Paradise Pride Sensation Cruise Line Azamara Azamara Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Carnival Age Tonnage Length 30.277 30.277 47.262 110 101.353 70.367 70.367 70.367 70.367 110.239 110 46.052 70.367 70.367 86 110 88.5 70.367 88.5 70.367 Cabins PassDens Crew 42.64 42.64 31.8 36.99 38.36 34.29 34.29 34.23 34.29 29.79 36.99 31.72 34.29 34.29 40.49 36.99 41.67 34.29 41.67 34.29 6 6 5.94 5.94 7.22 9.53 8.92 8.55 8.55 8.55 8.55 9.51 9.51 7.27 8.55 8.55 9.63 9.51 9.63 8.55 9.63 8.55 3.55 3.55 7.43 14.88 13.21 10.2 10.2 10.22 10.2 14.87 14.87 7.26 10.2 10.2 10.62 14.87 10.62 10.2 11.62 10.2 3.55 3.55 6.7 19.1 10 9.2 9.2 9.2 9.2 11.5 11.6 6.6 9.2 9.2 9.3 11.6 10.3 9.2 9.3 9.2 26 11 17 22 15 23 19 6 10 28 18 17 11 8 9 15 12 20

5. Full Model (5 Predictors, 6 Parameters, n=158) Regression Statistics Multiple R R Square Adjusted R Square Standard Error Observations 0.9589 0.9195 0.9169 1.0102 158 ANOVA df SS 1772.0 155.1 1927.1 MS 354.4 F 347.3 Significance F 0.0000 Regression Residual Total 5 152 157 1.0 Coefficients -1.9683 -0.0055 -0.0061 0.4191 0.6526 0.0279 Standard Errort Stat 0.9793 0.0144 0.0105 0.1176 0.0778 0.0133 P-value Lower 95%Upper 95% 0.0462 -3.9031 0.7056 -0.0340 0.5605 -0.0268 0.0005 0.1867 0.0000 0.4989 0.0378 0.0016 Intercept Age Tonnage Length Cabins Passdens -2.0099 -0.3785 -0.5833 3.5626 8.3882 2.0953 -0.0335 0.0230 0.0146 0.6516 0.8063 0.0542

6. Backward Elimination Model Based AIC (minimize) ( ) Model n SSE ( ) ( ) = + 2 parms(Model) Model ln AIC n 155.12 158 = + = Full Model (6 Parms, constant=0) 158 ln 2(6) 9.09 AIC + 155.26 158 155.54 158 = + = = = Round 2: 158 ln 2(5) 7.24 Round 3: 158 ln 2(4) 5.52 AIC AIC Full Model -age -tonnage <none> -passdens -length -cabins DF SS RSS AIC Round2 -tonnage <none> -passdens -length -cabins DF SS RSS AIC 1 1 0.146 0.347 155.26 155.47 155.12 159.6 168.07 226.93 7.241 7.446 9.092 11.591 19.764 67.2 1 0.276 155.54 155.26 160.66 168.13 227.07 5.521 7.241 10.64 17.817 65.299 1 1 1 5.397 12.864 71.803 1 1 1 4.48 12.953 71.806 Round3 <none> -passdens -length -cabins DF SS RSS AIC 155.54 161.91 169.92 369.72 5.521 9.866 17.495 140.323 1 1 1 6.373 14.383 214.177

7. Forward Selection (AIC Based) 1927.08 158 ( ) = = + = TOTAL SS 1927.08 Null Model 158 ln 2(1) 397.18 AIC Null Model +cabins +tonnage +length +age +passdens <none> DF SS RSS AIC Round2 +length + passdens + tonnage + age <none> DF SS RSS AIC 1 1 1 1 1 1742.21 1658.03 1546.6 542.66 46.6 184.88 269.05 380.49 1384.42 1880.48 1927.08 28.82 88.1 142.86 346.93 395.32 397.18 1 1 1 1 22.9636 14.9541 12.5135 5.4442 161.91 169.92 172.36 179.43 184.88 9.8661 17.4948 19.748 26.0989 28.8215 Round3 + passdens <none> + age + tonnage DF SS RSS AIC Round4 <none> + tonnage + age DF SS RSS AIC 1 6.3732 155.54 161.91 159.94 160.66 5.5212 9.8661 9.9317 10.6402 155.54 155.26 155.47 5.5212 7.241 7.4455 1 0.275559 1 0.074462 1 1 1.9702 1.2514

8. Stepwise Regression (AIC Based) Null Model +cabins +tonnage +length +age +passdens <none> DF SS RSS AIC Round2 + length + passdens + tonnage + age <none> - cabins DF SS RSS AIC 1 1 1 1 1 1742.21 1658.03 1546.6 542.66 46.6 184.88 269.05 380.49 1384.42 1880.48 1927.08 28.82 88.1 142.86 346.93 395.32 397.18 1 1 1 1 22.96 14.95 12.51 5.44 161.91 169.92 172.36 179.43 184.88 1927.08 9.87 17.49 19.75 26.1 28.82 397.18 1 1742.21 Round3 + passdens <none> + age + tonnage - length - cabins DF SS RSS AIC Round4 <none> + tonnage + age - passdens - length - cabins DF SS RSS AIC 1 6.373 155.54 161.91 159.94 160.66 184.88 380.49 5.521 9.866 9.932 10.64 28.821 142.859 155.54 155.26 155.47 161.91 169.92 369.72 5.521 7.241 7.446 9.866 17.495 140.323 1 1 1 1 1 0.276 0.074 6.373 14.383 214.177 1 1 1 1 1.97 1.251 22.964 218.571

9. Summary of Automated Models Backward Elimination Drop Age (AIC drops from 9.09 to 7.24) Drop Tonnage (AIC drops from 7.24 to 5.52) Stop: Keep Passdens, Length, Cabins Forward Selection Add Cabins (AIC drops from 397.18 to 28.82) Add Length (AIC drops from 28.82 to 9.87) Add Passdens (AIC drops from 9.87 to 5.52) Stop: Keep Passdens, Length, Cabins Stepwise Same as Forward Selection

10. All Possible (Subset) Regressions ' Number of parameters (including intercept) in Model p ( ) ( ) Regression(Model) Total SS Residual(Model) Total SS SS SS ( ) = = 2 Model 1 Goal:Maximize within reason R ( ) ( ) ( ) Residual(Model) Total SS SS 1 p n ( ) = 2 Adj- Model 1 Goal:Maximize R ( ) ' n ( ) Residual(Model) s SS ( ) ( ) = + = 2 Model 2 ' p Goal: ' where Residual(Full Model) C n C p s MS p p 2 ( ) Residual(Model) n SS ( ) ( ) = + + Model ln ln( ) ' constant Goal:Minimize BIC n n p

11. All Possible (Subset) Regressions (Best 4 per Grp) (Intercept)age tonnage length cabins passdens rsq adjr2 cp bic aic 1 1 1 1 2 2 2 2 3 3 3 3 4 4 4 4 5 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 0 0 0 1 0 1 0 0 0 1 1 1 1 0 1 0 0 0 0 1 0 0 0 1 1 1 0 1 1 1 0 0 1 0 1 0 0 0 1 1 1 0 1 1 1 0 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 0 0 1 0 0 1 0 0 1 1 1 0 1 1 0.904 0.86 0.803 0.282 0.916 0.912 0.911 0.907 0.919 0.917 0.917 0.913 0.919 0.919 0.917 0.913 0.92 0.903 0.859 0.801 0.277 0.915 0.911 0.909 0.906 0.918 0.915 0.915 0.911 0.917 0.917 0.915 0.911 0.917 27.16 109.64 218.84 1202.59 6.66 14.51 16.9 23.83 2.41 6.73 7.43 14.75 4.14 4.34 8.39 16.69 -360.2 -301.0 -246.2 -42.1 -376.1 -368.5 -366.2 -359.9 -377.4 -373.0 -372.3 -365.1 -372.6 -372.4 -368.3 -360.1 -367.7 -366.4 -307.1 -252.3 -48.3 -385.3 -377.7 -375.4 -369.1 -389.7 -385.3 -384.5 -377.4 -387.9 -387.7 -383.6 -375.4 -386.1 6

12. Cross-Validation Hold-out Sample (Training Sample = 100, Validation = 58) Fit Model on Training Sample, and obtain Regression Estimates Apply Regression Estimates from Training Sample to Validation Sample X levels for Predicted MSEP = sum(obs-pred)2/n Fit Model on Validation Sample and Compare regression coefficients with model for Training Sample PRESS Statistic (Delete observations 1-at-a-time) Fit model with each observation deleted 1-at-a-time Obtain Residual for each observation when it was deleted PRESS = sum(obs-pred(deleted))2 K-fold Cross-validation Extension of PRESS to where K groups of cases are deleted Useful for computationally intensive models

13. Hold-Out Sample nin = 100 nout = 58 Training Sample (Intercept) length cabins passdens Estimate Std. Error t value -1.9329 0.8315 0.3957 0.1409 0.6169 0.0557 0.0265 0.0135 Pr(>|t|) 0.0222 0.0060 -2.3250 2.8090 11.0740 < 2e-16 1.9600 Very similar coefficients for the 2 data sets 0.0529 Validation Sample Estimate Std. Error t value (Intercept) -1.6749 length 0.3746 cabins 0.6239 passdens 0.0232 Pr(>|t|) 0.0445 0.0161 0.0000 0.1245 0.8141 0.1507 0.0687 0.0149 -2.0570 2.4850 9.0870 1.5600 2 V n ( ) ' 1 n ^ y 2 = = = = = 2 0.6788 0.0002541524 MSEP y Bias ( ) iV iV T n = 1 i V 0.0002541524 0.6788 ( ) = = 2 Percent Bias of MSEP = 100 / 100 0.03744 (%) Bias MSEP

14. Testing Bias = 0 from Training data to Validation = = 0.01594216 0.830928 s 0.830928 58 s = = = 0.1091062 s n V 0.01594216 0.1091062 = = = 0.1461 t No evidence of systematic bias for samples s

15. PRESS Statistic ^ ^ ^ ^ = + + where regression was fit without case Y X X i pred 0( ) 1( ) ( ) i i p i 1 i ip ( } i i 2 n ^ = PRESS Y Y pred i ( } i i = 1 i PRESS n ( ) Compare with Residual for the full model MS ^ Y Y p ^ ( ) -1 i = th P = X X'X X' Note: where diagonal element of i Y Y ii p i pred i ( } i i 1 ii ( ) = = / 0.9801 Residual 0.96 PRESS n MS Model appears to be valid, very little difference between PRESS/n and MS(Resid)

16. K-fold Cross-Validation (k=10) Full Model Fold1 ObsNum Predicted CV_pred Crew 33 0.178 39 10.992 51 8.520 54 9.210 80 4.511 84 8.660 87 7.290 98 10.989 107 3.733 116 4.940 117 3.579 126 8.750 127 14.770 151 3.330 158 2.756 Fold10 ObsNum Predicted CV_pred Crew 16 12.038 29 8.350 38 6.912 44 11.910 45 8.329 46 6.219 56 5.358 64 6.781 65 6.750 68 13.394 92 9.009 110 11.200 145 1.704 147 3.403 155 8.570 CV_Res CV_Res -0.446 0.740 -0.556 -1.020 -0.674 0.153 -0.072 -0.665 -1.440 -0.253 -0.308 Total 1.200 -0.131 Model2 -0.462 Model3 3.430 Model4 18.689 15 1.246 Fold n(Fold) SSE(Fold) MSE(Fold) 29.70 61.80 8.80 3.97 10.30 7.51 11.90 8.92 2.13 18.70 163.73 -0.070 11.013 8.575 9.200 4.455 8.670 7.230 11.035 3.705 5.130 3.738 8.760 14.850 3.160 2.776 0.600 10.680 9.450 8.000 4.380 13.000 6.140 11.000 3.730 4.450 3.240 7.600 13.600 4.700 1.800 0.670 -0.333 0.875 -1.200 -0.075 4.330 -1.090 -0.035 0.025 -0.680 -0.498 -1.160 -1.250 1.540 -0.976 29.652 12.046 8.350 6.916 11.920 8.334 6.207 5.372 6.785 6.750 13.383 8.998 11.200 1.731 3.412 8.570 11.600 9.090 6.360 10.900 7.660 6.360 5.300 6.120 5.310 13.130 8.690 12.400 1.600 2.950 12.000 1 2 3 4 5 6 7 8 9 15 16 16 16 16 16 16 16 16 15 158 1.98 3.86 0.55 0.25 0.65 0.47 0.74 0.56 0.13 1.25 1.036 10 158 158 158 163.26 160.75 160.38 1.033 1.017 1.015 SSE # Obs MSE(CV) SSE # Obs MSE(CV) 15 1.977 E Y E Y = = + + + + + + + + + = = + + + + + + + Model 1: Model 2: E Y A T L C P E Y T L C P 0 0 A T L C P T L C P Model 3: Model 4: A L C P L C P 0 0 A L C P L C P