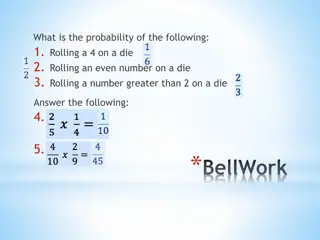Probability Rules and Practice Problems
Explore the fundamental rules of probability, including addition and multiplication rules, through practice problems and scenarios. Topics covered include rolling dice, drawing cards, and calculating probabilities of specific outcomes. Includes warm-up exercises and homework assignments.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Homework (AP) Pg.309 #43, 47, 49 Agenda Warm Up Yesterday s worksheet Checkup Check, copies The Five Rules of Probability Worksheet time Sally Clark & crib deaths Copies Independent vs. disjoint Start conditional probability? Exit Pass 10 min 10 min 10 min Homework (reg) Pg.430 #6.45, 6.47, 6.51 15 min 15 min 10 min 10 min 15 min 5 min
Warm Up 1. P(rolling more than a 3 on a standard die). 2. P(rolling at least a 3 on a standard die). 3. What does your answer to #2 mean? 4. Challenge. In a game of Yahtzee, you roll five standard dice. What is the probability of getting a Yahtzee! , which is 5 identical numbers?
4 of 7 #4: The Addition Rule The probability of Event A or Event B is the sum of their probabilities, minus their overlap . P(A or B) = P(A) + P(B) P(A and B). Can be simplified to P(A) + P(B) if disjoint (meaning no overlap) Written as P(A B), the union of A and B Example: What is the probability of drawing a Jack or a diamond from a standard deck? Door/Window. If you roll a standard die . 1. Door: P(even number or 5) on standard die 2. Window: P(even number or 4) on standard die 3. Door: P(2 or 3) on standard die 4. Window: P(2 on standard die or Heads on coin)
5 of 7 #5: The Multiplication Rule Probability of Event A and Event B is product of the probability of A and the probability of B given that A has happened. Written as P(A B) = P(A) P(B|A), intersection of A and B If A and B are independent, the rule is P(A B) = P(A) P(B) Example: What is the probability of getting an Ace and then a Jack? What is the probability of getting an Ace and a Jack? Door/Window. What s the probability? 1. Door: rolling two dice and getting two 6 s 2. Window: flipping three Heads 3. Door: drawing two cards, getting a Queen and a King 4. Window: drawing two cards, getting the Ace of spades and then the two of hearts 5. Challenge . Drawing two cards, getting a Queen and a heart.
0652 . 0 #5 : Queen and Heart You could get a Queen of Hearts on the first draw. OR You could get a non-Queen Heart, and then a Queen. OR You could get a non-Heart Queen, and then a Heart. OR You could get a bad card, and then a Queen of Hearts. 1 + 51 52 12 4 3 13 35 1 + + 52 52 51 52 51
Worksheet time Groups of 4. Do #7-12 on the back of your cheat-sheet. When you re done, check answers with me. If you are correct, try #13-18(conditional probability) Use pencil.
Liar, liar, pants on fire You need a calculator with Math:PRB:RandInt I am your manager, you are my employees. The accounting department reports that about 10% of my employees are stealing! I want to fire the thieves, obviously. I buy a lie detector machine, 80% accuracy. If you are a thief, you will fail with probability 0.8 If you aren t a thief, you ll pass with probability 0.8
Liar, liar, pants on fire Are you a thief? (10% chance) Use your calculator to roll a 1-10 die 1 Thief! 2-10 Not a thief Do not reveal what you really are. What does the lie detector say? (80% accurate) Use your calculator to roll again 1,2 Lie detector FAILS. 3-10 Lie detector succeeds. You are fired if either of these happens: If you are a thief, and the lie detector succeeds, it says THIEF! If you are honest, but the lie detector fails, it still says THIEF! When I say, you will stand up if you are fired. Do not reveal what you really are.
Liar, liar, pants on fire What percent (%) of the fired students do you think are really thieves? 10% of employees are stealing. Lie detector, 80% accuracy. Says: Honest 0.8 Honest 0.9 Says: Thief! 0.2 Says: Thief! 0.8 Thief 0.1 Says: Honest 0.2
Liar, liar, pants on fire What percent (%) of the fired students do you think are really thieves? 10% of employees are stealing. Lie detector, 80% accuracy. . 0 72 Says: Honest 0.8 Honest . 0 . 0 18 08 0.9 Says: Thief! 0.2 Says: Thief! 0.8 Thief 0.1 . 0 02 Says: Honest 0.2
Conditional Probability # possible successes # possible outcomes Example (from previous activity) Given that the lie detector has gone off , what are the chances it s right, and you ve caught a thief? Another example: A survey of college students found that 40% like country music, 30% like rock music, and 10% like both. 1. What is the probability that a student likes rock music, given that we know they like country music? 2. What is the probability that a student likes rock music, given that they don t like country music.
Another example Department and gender at RCHS. M=Male, F=Female, X=Math, E=English Math (X) 7 7 14 English (E) 5 13 18 TOTAL 12 20 32 Male (M) Female (F) TOTAL 1. P(F E) = 2. P(M X) = 3. P(E M) = 4. P(M F) =
Finish worksheet #13-18
Crib death, and Sally Clark. Why it s important to check for Independence.
6 of 7 Independent vs. Disjoint, 1 of 2 Two events are independentif whether one occurs does not change the probability that the other occurs. P(A) = P(A|B) Yes: drawing a Jack, replacing, shuffling, drawing again No: drawing a Jack, then drawing again Doesn t mean they can t affect each other just end up unchanged. Weird Yes: You flip 3 coins. Let A = {Obtain 2+ H's} = {HHT, HTH, THH, HHH}, and C = {All flips identical} = {HHH, TTT}. P(A) = ____ P(A|C) = _____ Door/Window. 1. Two events that are probably independent. 2. Two events that are probably not independent
7 of 7 Independent vs. Disjoint, 2 of 2 Two events are disjoint ( mutually exclusive ) if they have no outcomes in common. Yes: drawing a Jack or a Queen No: drawing a Jack or a heart Door/Window. 1. An example of two events that are disjoint 2. An example of two events that are not disjoint
Homework (AP) Pg.309 #43, 47, 49 Exit Pass 1. P(rolling a 3 or a 4 on one die) 2. P(rolling a sum of 11 on two dice) 3. P(rolling an even & odd number on two dice) 4. P(flipping Heads and rolling a 4) 5. P(flipping Heads or rolling a 4) 6. If I pick a card, what is the probability that it is a Jack? 7. Let s say I get a Jack and set it aside. If I pick another card, what is the probability that it s a Queen? 8. Let s say I shuffle the cards back in and pick another card. What is the probability that it s a King?
