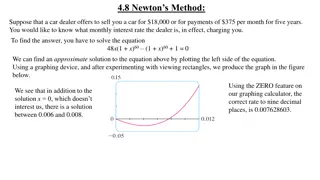
Practice Trial and Improvement Method in Equations

Enhance your skills in finding approximate solutions to equations through trial and improvement methods. Understand the concept of number lines, inequalities, and how to refine answers gradually. Practice solving equations by testing different values and determining the most accurate solutions. Explore examples and methods to identify solutions within specific ranges.

• Equations
• Trial and Improvement
• Number Lines
• Inequalities
• Approximate Solutions

malonna Follow

Uploaded on Oct 09, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. Dr Frost Year 8 Trial and Improvement Objectives: Be able to find approximate solutions to more difficult equations by gradually refining our answer.

2. Ranges on Number Lines We can use number lines to express a range of values that are possible. Means the value is included. Means the value is NOT included. A weight ? being 6kg correct to the nearest 2kg As an inequality: On number line: ? 5 ? < 7 ? 2 4 6 8 9 A length ? being 4.1 correct to 1dp On number line: As an inequality: ? 4.05 ? < 4.15 ? 3.9 4.0 4.1 4.2 4.3

3. Starter You want to solve the equation: ? ? 2 = 61 Use trial and error to find the most accurate value of ? that you can. ? = 8.874007874011... ?

4. Trial and Improvement How did you know when to try bigger or smaller values of x on the next step? Solve ?(? ?) = ?? x = 5 x = 10 x = 8 x = 8.5 x = 8.8 x = 8.9 x = 8.87 x = 8.88 : 5(5-2) = 15 : 10(10-2) = 80 : 8(8-2) = 48 : 8.5(8.5-2) = 55.25 : 8.8(8.8-2) = 59.84 : 8.9(8.9-2) = 61.41 : 8.87(8.87-2) = 60.94 : 8.88(8.88-2) = 61.09 Too small Too large Too small Too small Too small Too large Too small Too large ? ? ? ? ? ? ? ?

5. Showing theres a solution Show that ?3+ 2? = 7 has a solution between 1 and 2. When ? = 1, ?3+ 2? = 3. Since 3 < 7, this is too small. When ? = 2, ?3+ 2? = 12. Since 12 > 7 this is too big. Thus solution must lie between 1 and 2. ? Show that ?2 2? = 0 has a solution between 1 and 3. When ? = 1, ?2 2? = 1. Too small. When ? = 3, ?2 2? = 5. Too big. Thus solution must lie between 1 and 3. ?

6. When to stop? Solve x(x-2) = 61 x = 8.87 x = 8.88 : 8.87(8.87-2) = 60.94 : 8.88(8.88-2) = 61.09 Too small Too large Suppose the we wanted the answer correct to 2dp. Could we stop at this point? What value would we choose for x? x = 8.875 : 8.875(8.875-2) = 61.02 Too large ? We know therefore that the value of x lies between: 8.87 and 8.875. To 2dp the solution must be 8.87. ? ?

7. Another Example A container in the shape of a cuboid with a square base is to be constructed. The height of the cuboid is to be 2 metres less than the length of a side of its base and the container is to have a volume of 45 cubic metres. a) Taking ? metres as the length of a side of the base, show that ? satisfies the equation ?3 2?2 45 = 0 b) Use a trial and improvement method to find the solution of the equation ?3 2?2 45 = 0 that lies between 4 and 5. Give your answer correct to two decimal places. c) Find the height of the container correct to the nearest cm. : 4.363 2 4.362 45 = 0.137 Too small : 4.373 2 4.372 45 = 0.260 Too big : 4.3653 2 4.3652 45 = 0.061 Too big ? ? = 4.36 ? = 4.37 ? = 4.365 So ? = 4.36 ?

8. Exercises Edexcel GCSE Mathematics Page 25B Page 419 Q1a, 2a, c, 4, 6, 8, 10

9. What have we learnt? We can find solutions to equations by gradually improving our estimate. Solve 2x = 14 to 2dp ... x = 3.80 x = 3.81 x = 3.805 : 23.80 = 13.93 : 3.32 + 3.3 = 14.03 : 3.252 + 3.25 = 13.98 Too small ? Too small Too large So x = 3.81 to 2dp ? ? Solve x2 = 4 + x to 1dp Solve x2 x = 4 ... x = 2.5 : 2.52 2.5 = 3.75 x = 2.6 : 2.62 2.6 = 4.16 x = 2.55 : 2.552 2.55 = 3.95 Too small Too large Too small ? So x = 2.6 to 1dp ?

10. Puzzle A square of side length 2 is cut out of a circle of radius x. The resulting area is x. Form an equation involving the area, and hence use trial and improvement to determine x correct to 1dp. Equation for area: x2 4 = x x2 x = 4 ? x 2 x = 1.2 : 3.324 x = 1.3 : 4.009 x = 1.25 : 3.659 Too small Too large Too small ? 2 So x = 1.3 to 1dp ? Area = x Work in 3s/4s (but you need to each individually show your working in your book)