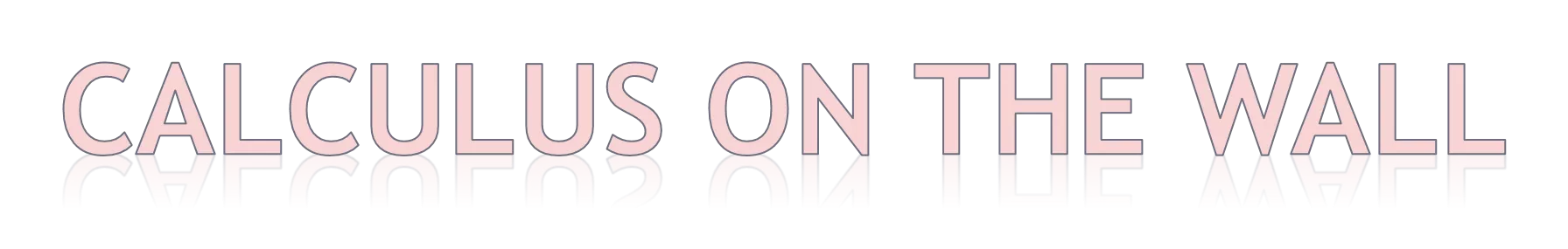Parametric and Polar Equations in Calculus

Dive into the world of parametric and polar equations with insights on graphing, tangents, conversions between polar and rectangular coordinates, and finding the area enclosed by polar curves. Discover the power of these mathematical representations in understanding complex curves and functions.

• Calculus
• Parametric Equations
• Polar Equations
• Graphing
• Tangents

fitzpatr Follow

Uploaded on Oct 07, 2024 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. mastermathmentor.com presents CALCULUS ON THE WALL Helping students learn and teachers teach 18. Parametric and Polar Equations Created by: Stu Schwartz Sample Version Un-narrated Graphics: Apple Grapher: Version 2.3 Math Type: Version 6.7 Intaglio: 2.9.5a Fathom: Version 2.11

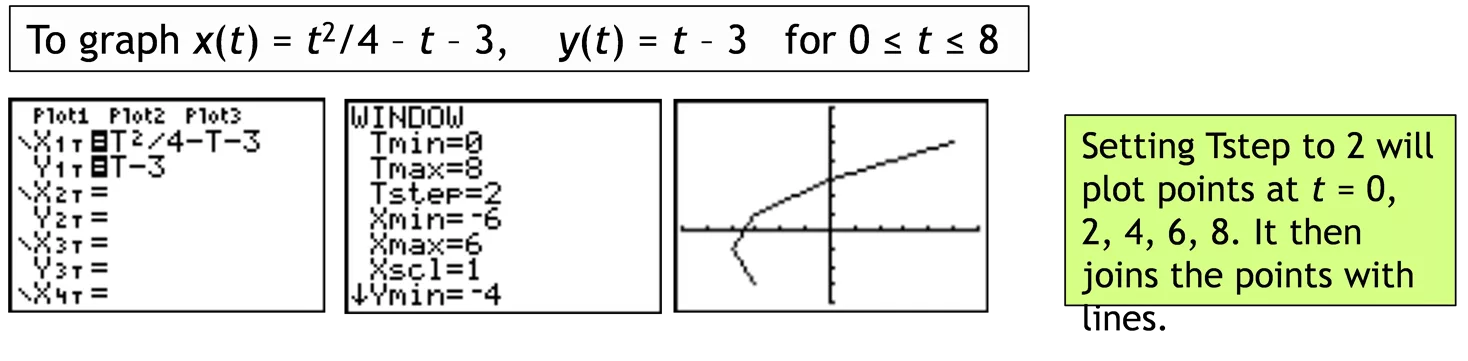
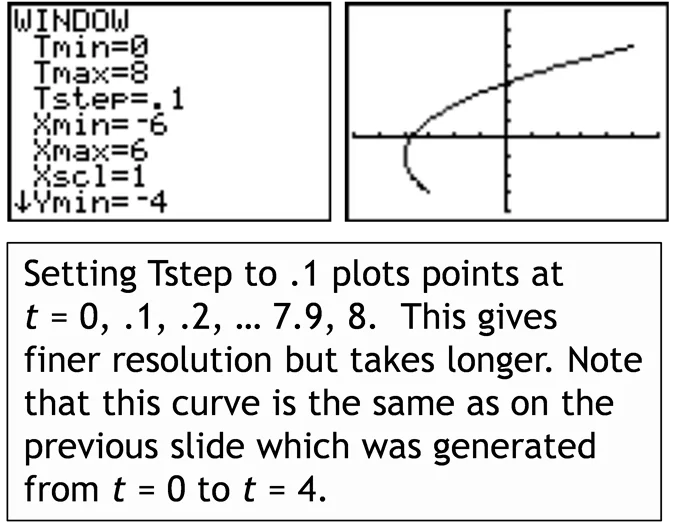
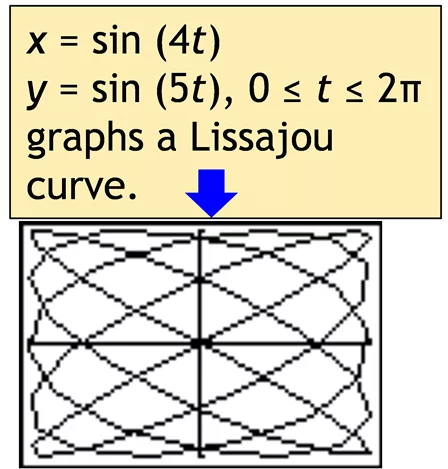
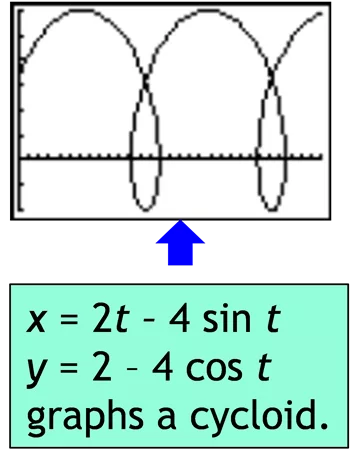
2. Using the Calculator The TI-84 calculator can graph parametric equations. Pressing M allows you change to parametric form. To graph x(t) = t2/4 t 3, y(t) = t 3 for 0 t 8 Setting Tstep to 2 will plot points at t = 0, 2, 4, 6, 8. It then joins the points with lines. x = sin (4t) y = sin(5t), 0 t 2 graphs a Lissajou curve. Setting Tstep to .1 plots points at t= 0, .1, .2, 7.9, 8. This gives finer resolution but takes longer. Note that this curve is the same as on the previous slide which was generated from t = 0 to t = 4. x = 2t 4 sin t y = 2 4 cos t graphs a cycloid. www.mastermathmentor.com

3. Horizontal and Vertical Tangents A parametric equation will have horizontal tangents at values of t where dy/dt = 0. It will have vertical tangents at values of t where dx/dt = 0. At values of t where both dy/dt = 0 and dx/dt = 0, no conclusion can be made. x = t2-t -2 and y = 2t3-6t +1 dx dt= 2t -1, dy Vertical: 2t -1= 0 t =1 x = t 2 -2cost and y = 2-2cost dx dt= Vertical: sint =- 2 2 Horizontal: 2sint = 0 t = 0,p,2p,3p,... 2 +2sint, dy dt= 6t2-6 dt= 2sint t =5p -9 4,-7 4,7p 4,13p ,15p 4 Pt: ... 2 4 ( 4 ), 0,5 ( ) Horizontal: 6t2-6 = 0 t = 1 Pts: -2,-3 t = (6.44,4) t = 3 (15.33,4) t = 1 (0,5) t = 5 /4 (6.97,3.41) t = 13 /4 (15.85,3.41) t = 7 /4 (15.25,0.59) t = 7 /4 (6.36,0.59) t = 1/2 ( 9/4, 7.4) (-9/4,-7/4) t = 0 (-2,0) t = 2 (6.89,0) t = 4 (15.77,0) t = 1 ( 2, 3) www.mastermathmentor.com

4. Polar Rectangular Equation Conversions Rectangular coordinates are superior for showing linear functions while the strength of polar equations is to show curves and non-functions. But in many cases, one form can be changed to the other. 4 3x- 4y = 8 3rcosq - 4rsinq = 8 y = x2 rsinq = r2cos2q r =sinq cos2q r = 4cos2q +sin2q 4 4cos2q +sin2q 4r2cos2q +r2sin2q = 4 4x2+ y2= 4 r2= 8 r = 3cosq - 4sinq www.mastermathmentor.com

5. Area Enclosed by Polar Curves Find the area between the inner and outer loops of r= 2 sin + 2 We first view how this graph is produced. (Click on graph to animate.) At = 0, the graph is at the point ( 2, 0) and travels counter-clockwise around the outer loop. It reaches the pole (origin) at the point (5 /4, 0). It then travels the inner loop from 5 /4 to 7 /4, and then continues the outer loop back to the point ( 2, 0) at = 2 . 5p 4 7p 4 ( ) ( ) Half Outer Loop: A =1 Inner Loop: A =1 2dq 2dq 2sinq + 2 2sinq + 2 Area between loops: 12.425-0.142 =12.283 2 2 p 2 ( 5p 4 ( 5p 4 3p 2 ) ) 2dq 2dq Full Outer Loop: A = 2sinq + 2 =12.425 Inner Loop: A = 2sinq + 2 = 0.142 p 2 5p 4 www.mastermathmentor.com

6. Purchase the full version - 19 slides Content: Parametric & Polar Equations www.mastermathmentor.com Powerpoint slides to help teach in the classroom Only $10.95 for the full presentation of 19 content slides. (download version) You receive: A narrated version (78 megs) An un-narrated version (5 megs) A PDF of the narration used if you want to provide the commentary Note: Downloading the full presentation may require high-speed internet. Or purchase the entire set of MasterMathMentor.com BC Calculus On the Wall Powerpoint presentations - Only $69.95 - sent to you on a 2-gig flash drive. Topics cover: L Hospital s Rule Integration Techniques Euler s Method & Logistic Growth Parametric and Polar Equations Vector-Valued Functions Taylor Polynomials Infinite Series Power Series www.mastermathmentor.com