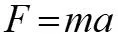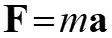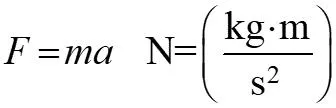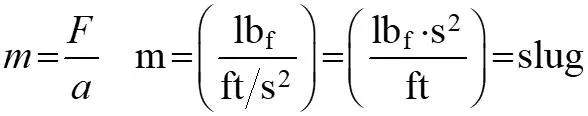Newton's Second Law of Motion
Exploring Newton's Second Law of Motion which states that an unbalanced force acting on a particle causes acceleration proportional to the force. The law is expressed as F=ma, highlighting the relationship between force, mass, and acceleration. Additionally, the concept of gravitational attraction and the equation of motion are discussed in relation to forces, mass, and acceleration.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Newtons Second Law of Motion So far we have done a bunch of particle motion. You can do things like: 1D motion s(t) 2D and 3D motion in rectangular coordinates x(t), y(t), and z(t) 2D and 3D chain rule y(x), x(t) 2D and 3D motion in normal and tangential coordinates n(t), t(t) 2D and 3D motion in polar and cylindrical coordinates r(t), (t), z(t) Within particle motion we have considered position, velocity, and acceleration. But we haven t yet talked about forces. If we prescribe a path of motion, what forces are necessary to make that happen? If we put external forces on a particle, what is the resulting motion?
13.1 Newton s Second Law of Motion When an unbalanced force acts on a particle, the particle will accelerate in the direction of the force with a magnitude that is proportional to the force. Newton s Second Law: F ma = This is Newton s Equation of Motion Mass is a quantitative measure of the resistance of the particle to a change in velocity. = F a m acceleration is in the same direction as force. kg m s Units of force in the SI (System International) system are derived from Newton s E.O.M. F ma = N= 2 lb ft s lb s F a 2 Units of mass in FPS (Foot Pound Second) system are derived from Newton s E.O.M. f f ft = = = = m slug m 2
13.1 Newton s Second Law of Motion Newton s Law of Gravitational Attraction: when an unbalanced force acts on a particle, the particle will accelerate in the direction of the force with a magnitude that is proportional to the force. m m mass of particle 1 mass of particle 2 distance between particle centers 1 r 2 F G = ( EQ 13-1) 2 Typically only consider gravitational force between earth and particles because: Universal Gravitational Constant G = 66.73(10 )m (kg s ) 12 3 2 ?earth ?particle Mass A relative quantity, manifests as weight Weight Combination of mass and a gravitational field Mass and Weight = = = m mass of particle mass of earth m m m =acceleration due to gravity @ sea level & latitude = 45 2 2 1 = g Gr Let: Define: 2 So now a particle in Earth s gravitational field: weight is the force caused by Earth s gravity acting on the particle m m Gm r 1 r 2 2 F G = = = = or: (E Q 13-2) m mg W mg 2 2
13.1 The Equation of Motion Mass, Acceleration, and Force Units: Systeme International (SI) Units Foot-Pound-Second (FPS) Units lb s W g 2 f ft = = slug slug m mass kg ( E Q 13-3) kg m s = force N lb f 2 ( ) acceleration 9.81 m s 32.2 ft s g 2 2 A body of 1 kg of mass has a we i g ht of 9 .81 N A body of 32.2 lb of weight has a mass of 1 slug ( f ( ) = m w a = W ma ) Mass is fundamental Force is derived Force is fundamental Mass is derived
13.2 The Equation of Motion For the general case with multiple forces, we can write: The Equation of Motion sum of all forces R= F F resultant force F = a EQ 13-4) ( m And the equation of motion can be written: A free-body diagram graphically accounts for the magnitude and direction of each force acting on the particle. A kinetic diagram graphically accounts for the magnitude and direction of the vector ma
13.2 The Equation of Motion Inertial Reference Frame (or Newtonian Reference Frame) When applying the equation of motion, the acceleration of a particle must be measured with respect to a reference frame that is fixed or translates with a constant velocity. Measurement of a particle acceleration will be the same from any inertial reference frame. Dynamics problems concerned with motions on or near the surface of the earth may be solved by using an inertial frame which is assumed fixed to the earth. The accelerations created by the rotations of the earth (about own axis, sun, galaxy, etc) are relatively small and can be neglected for most applications.
The Equation of Motion Dr. Dan .I don t believe you. Prove it! - Imaginary Student Challenge accepted! What is the normal and tangential acceleration of a particle on the surface of the Earth (relative to the center of the Earth)? = + a u u (EQ 12-18) a a t t n n = v (EQ 12-19) a v ??= 0 constant velocity at surface t 2 = (EQ 12- 20) a ? = ? ? n ?????? ? = 3960 ????? 1 ?? ?????? 2? ??? ? ?????? 3960 ????? 5280 ???? 1 ????? ? = = 1520 ???? 3600 24 2 ?? 1520 20,908,800 ??= 0.11 ??? ?? ??= ???2 pretty small compared to gravitational constant
13.3 Equation of Motion for a System of Particles Equation of Motion for a System of i Particles Including internal and external forces: + = F f i i a m i i = The summation of all internal forces will be zero, thus: F i i a m i Now define a position vector to the center of mass of the particles: = = r i i r where m m m m G i = Differentiating twice with respect to time gives: a i i a m m G F Combining this result with the previous equation of motion: = a m G (EQ 13-6)
In-Class Practice Problem 1 Statics problem? No numbers? Key words? What does equilibrium equation look like for Mass B? What does equation of motion look like for Mass B?
In-Class Practice Problem 1 External Forces Motion
In-Class Practice Problem 2 Did you learn about coefficient of friction already? (Statics, Physics) Which block moves more? What does equation of motion for each block look like?
In-Class Practice Problem 2 For Block A Note Direction!
In-Class Practice Problem 2 For Block B Note Direction!
Next Homework Apply Equations of Motion Could be given a(t), then need to use particle motion equations to find position and/or velocity at a specific time Could be given mass, friction, initial velocity Find R, time, etc. Along with answers I ve also given some intermediate answers so you can check along the way.