Minimum spanning tree
In the realm of graph theory, the quest for the minimum spanning tree in weighted undirected connected graphs is a crucial pursuit. This involves finding a connected acyclic subgraph with the least total weight, paving the way for efficient network optimization and resource allocation.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
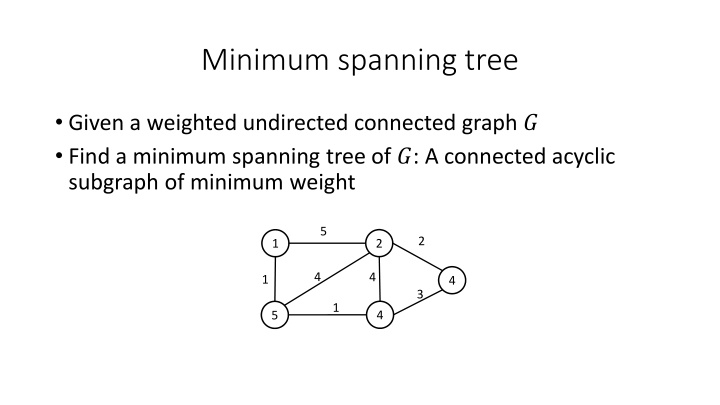
Minimum spanning tree Given a weighted undirected connected graph ? Find a minimum spanning tree of ?: A connected acyclic subgraph of minimum weight 5 2 2 1 4 4 1 4 3 1 4 5
Minimum spanning tree Given a weighted undirected connected graph ? Find a minimum spanning tree of ?: A connected acyclic subgraph of minimum weight 5 2 2 1 4 4 1 4 3 1 4 5
Safe edges Let ? be a set of edges contained in an MST ? ?,? is safe for ? if ? ?,? is also contained in an MST
Cuts A partition of ?, (?,? ?)
Cuts A partition of ?, (?,? ?)
Respects A cut (?,? ?)respects? ? if no edges ?,? ? is such that ? ? and ? ? ?
Recognizing safe edges Thm 1: Let ? be a set which is contained in an MST. The lightest edge that crosses a cut (?,? ?) that respects? is safe for ? Proof:
Generic MST Cor 1: The lightest edge incident to any connected component of A is a safe edge
Generic MST Maintains a forest, induced by ? Executed ? 1 time Each iteration reduces the number of connected components
Generic MST Cor 1: The lightest edge incident to any connected component of A is a safe edge
The algorithms of Kruskal and Prim Kruskal maintains a forest and adds the lightest edge that reduces the number of connected components Prim maintains a single tree and adds the lightest edge incident to this tree
Correctness of Kruskals algorithm 1) Each edge added by the algorithm is safe with respect to the (current) A 2) When the algorithm stops A is an MST (no safe edge remaining) (1) Follows since when we add an edge e=(u,v) it is the lightest in a cut between the component of the forest induced by A containing u and its complement (using cor1) (2) Follows since otherwise A is a forest least two disconnected trees, that are connected in G and should have been combined by the algorithm when an edge between these components has been considered.
Running time of Kruskals algorithm ?(? log?) The cost of sorting dominates
Prims algorithm decrease-key(Q,v,w(u,v))
Correctness of Prims algorithm Vertices in ? are still isolated, Vertices in ? ? are in the tree whose edges are A = { ?.?,? ? ? ?} ?.??? for ? ? is the weight of the lightest edge that connects it to the current tree
Analysis of Prims algorithm We make ?(?) insertions and extract-min operations on the heap Then for each edge we may do a decrease-key Running time is dominated by the operations on the heap ?(? log?) with binary heaps ?(? + ?log?) with Fibonacci heaps decrease-key(Q,v,w(u,v))