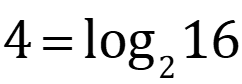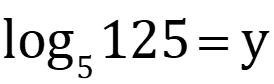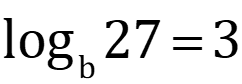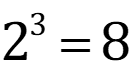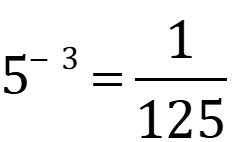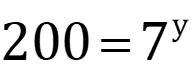Logarithmic Properties and Rules
Check up
Change to Exponential Form
1)
2)
3)
Check up 2
Change to equivalent logarithmic form:
3)
4)
5)
Check up 3
Evaluate without a calculator
5)
6)
Check up 4
What base does the logarithm have?
9) ln 5
10) Log 16
Check up 5
Find the domain
11) f(x) = log (2 – x)
Chapter 9 Section 4
Properties of Logarithms
Page 704
The Product Rule
Expanding a Logarithmic Expression
Write a logarithm with more than one logarithm
Example:
Expanded:
Expand the following
a)
b) log(100x)
Condensing Logarithmic Expressions
Write the logarithm as a single logarithmic expression
Example:
Condense the following:
•
Solution:
• Use the product rule
Condense
a)
log
7
19 + log
7
5
b)
ln 7 + ln x
Quotient Rule
•
Same Base:
Let b, M, and N be positive real numbers with b ≠ 1
The logarithm of a quotient is the difference of the logarithms.
Example
•
Expand the logarithm
Solution:
Simplify
5 – ln 11
Expand the following
a)
b)
Condense the following:
a)
log
7
19 – log
7
x
b)
ln e
3
– ln 7
The Power Rule
Exponential Expression is raised to a power, multiply the exponents.
The Power Rule
Let b, M, and N be positive real numbers with b ≠ 1 and p any real
number
Example
a)
Expand the logarithm
Solution:
power becomes the coefficient.
b) Expand:
Solution:
5 log(4x)
Review
Expand the following:
a)
b)
c)
Condensing Logarithmic Expressions
Write the logarithm as a single logarithmic expression
Example:
Condense the following:
•
Solution:
• Use the product rule
Write as a single logarithm - Condense
a)
log 25 + log 4
b)
c) 2 log (x – 3) – log x
The Change-of Base Property
Calculators give values of both common logarithms and natural
logarithms. To find the value of any other base, this property is used.
For any logarithmic bases ‘a’ and ‘b’, and any positive numbers M,
Example
Evaluate:
Solution: Since the calculator can only evaluate logarithms with base 10
and base ‘e’, pick the base
Base 10
Base e
Use the calculator and evaluate the quotient.
Try
Evaluate. Give the answer to 3 decimal places.
a)
b) log
63
17
Natural logarithms
•
The rules hold for the natural logarithm.
Summary
Logarithmic properties, rules, and examples such as converting to exponential form, evaluating without a calculator, finding domains, and using product and quotient rules. Learn about expanding and condensing logarithmic expressions.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Check up Change to Exponential Form 4=log216 1) log5125= y 2) 3) logb27=3
Check up 2 Change to equivalent logarithmic form: 23=8 3) 1 5-? 3= 4) 125 200=7y 5)
Check up 3 Evaluate without a calculator log264 5) log819 6)
Check up 4 What base does the logarithm have? 9) ln 5 10) Log 16
Check up 5 Find the domain 11) f(x) = log (2 x)
Chapter 9 Section 4 Properties of Logarithms Page 704
The Product Rule Properties of exponents correspond to properties of logarithms. ?? ??= ??+? So Let b, M, and N be positive real numbers with b 1 ( )=logbM+logbN logbMN The logarithm of the product is the sum of the logarithms
Expanding a Logarithmic Expression Write a logarithm with more than one logarithm Example: log47 5 ( ) Expanded: log47+log45
Expand the following ( ) log67 11 a) b) log(100x)
Condensing Logarithmic Expressions Write the logarithm as a single logarithmic expression Example: Condense the following: Solution: Use the product rule log24x log24+log2x
Condense a) log719 + log 75 b) ln 7 + ln x
Quotient Rule bm bn=bm-n Same Base: Let b, M, and N be positive real numbers with b 1 M N =logbM-logbN logb The logarithm of a quotient is the difference of the logarithms.
Example Expand the logarithm e5 11 ln Solution: ln? e5-ln? 11 Simplify 5 ln 11
Expand the following 19 x log7 a) e3 7 b) ln
Condense the following: a) log 719 log 7x b) ln e3 ln 7
The Power Rule Exponential Expression is raised to a power, multiply the exponents. ( ) n=bmn bm The Power Rule Let b, M, and N be positive real numbers with b 1 and p any real number logbMp=p? logbM
Example a) Expand the logarithm log574 Solution: 4log57 power becomes the coefficient. log 4x ( ) 5 b) Expand: Solution: 5 log(4x)
Review Expand the following: ( ) logbx2y a) x2w d2 logb b) log 100x c)
Condensing Logarithmic Expressions Write the logarithm as a single logarithmic expression Example: Condense the following: Solution: Use the product rule log24x log24+log2x
Write as a single logarithm - Condense a) log 25 + log 4 ( ) 1 2log2x+4log2x-1 b) c) 2 log (x 3) log x
The Change-of Base Property Calculators give values of both common logarithms and natural logarithms. To find the value of any other base, this property is used. For any logarithmic bases a and b , and any positive numbers M, logbM=logaM logab
Example log5140 Evaluate: Solution: Since the calculator can only evaluate logarithms with base 10 and base e , pick the base Base 10 Base e log5140=ln? 140 log5140=log? 140 ln? 5 log? 5 Use the calculator and evaluate the quotient.
Try Evaluate. Give the answer to 3 decimal places. log72506 a) b) log6317
Natural logarithms The rules hold for the natural logarithm.
Summary Product rule: logb(MN) = logbM + logbN Quotient rule: logb Power rule: logbMp= p logbM Expanding logarithmic Expressions Condensing logarithmic expressions Change of Base Property: logbM = ????? Natural logarithms rules. ? ? = logbM logbN ?????
