Linked Lists and Binary Search Trees Overview

This content delves into the concepts of linked lists and binary search trees, covering their structures and functionalities. It provides a comprehensive understanding of how these data structures work, their applications, advantages, and implementation in software development. The discussion highlights the importance of mastering linked lists and binary search trees, offering insights into efficient data organization and retrieval strategies. Whether you're a beginner or looking to deepen your knowledge, this content serves as a valuable resource for learning and mastering these fundamental concepts.

• Data Structures
• Linked Lists
• Binary Search Trees
• Software Development
• Applications

princesto Follow

Uploaded on Feb 20, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

1. IAT 265 Linked Lists, Binary Search Trees July 2, 2015 IAT 265 1

2. Data Structures With a collection of data, we often want to do many things Store and organize data Go through the list of data and do X per item Add new data Delete unwanted data Search for data of some value Give me Smith s phone number July 2, 2015 IAT 265 2

3. Arrays 0 1 2 3 4 5 6 Store data arr[3] = 33 Iterate (go thru): for( i = 0 ; i < 10 ; i++) sum = sum + arr[i] ; Add arr[last] = newNumber ; last++ ; Delete i for( j = i+1 ; j < last ; j++ ) arr[j-1] = arr[j] ; last -- ; Search for 42 for( i = 0 ; i < last ; i++ ) if( arr[i] == 42 ) SUCCESS ; July 2, 2015 IAT 265 3

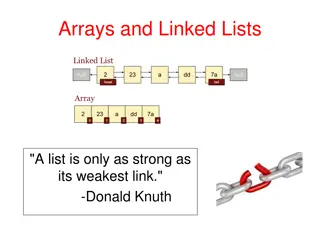
4. First Pointer 0 P 1 P 3 P Linked List 4 P 2 P A chain of nodes, where each node links to the next Node Has: Value Pointer to Next Node Inserting a new item is faster than array move pointers around Deleting is also faster than array Searching takes time Must go link by link from Node to Node July 2, 2015 IAT 265 4

5. First Pointer 0 P 1 P 3 P Linked List 4 P 2 P class Node { int value ; Node next ; } Node n, first ; Add n = new Node( 12 ); n.next = first ; first = n ; Delete n1 n1 = n.next ; n.next = n1.next ; Store data n.value = 33 Iterate: n = first ; while( n!= NULL ) { sum += n.value ; n = n.next; } Search 42 n = first ; while( n!= NULL ) { if( n.value == 42 ) SUCCESS ; n = n.next ; } July 2, 2015 IAT 265 5

6. Runtime Often, we care about the time that computation takes It s ok if unimportant things run slow Important stuff needs to go fast Stuff that gets run all the time The Inner Loop is a slang term I use July 2, 2015 IAT 265 6

7. Whats Important YOUR time is important Runtime != Creation Time If any old algorithm will work, AND you re only going to do it once or twice Use it! If you re going to run it millions of times Think about the algorithm! July 2, 2015 IAT 265 7

8. Trees A Tree is a node-link structure It is built to enable fast searching What Write Store Like linked list Go Thru More complex Add More complex Delete More complex Search A little complex Much faster Runtime As fast As fast A little slower A little slower July 2, 2015 IAT 265 8

9. Binary Search Tree July 2, 2015 IAT 265 9

10. Root Pointer Binary Search Tree LP 3 RP Each Node has two links left and right child Top node is root Node without children is leaf Binary meaning two children Search tree because of the node arrangement LP 5 RP July 2, 2015 IAT 265 10

11. Binary Search Tree Root Pointer LP 3 RP LP 5 RP LP 1 RP LP 2 RP LP 0 RP LP 4 RP LP 6 RP July 2, 2015 IAT 265 11

12. Binary Search Tree For Any node n To the left All child values are Less Thann To the right All child values are Greater Thann This is a recursive definition!!! July 2, 2015 IAT 265 12

13. Binary Search Tree July 2, 2015 IAT 265 13

14. Nodes Typically, each node has 3 or 4 parts: The key (names in pictures) The payload that goes with the key (not shown) The left child pointer (possibly null) The right child pointer (possibly null) July 2, 2015 IAT 265 14

15. Binary Search Tree Search class BNode { int BNode left, right ; } BNode root, cursor ; key ; cursor = root ; while( cursor != null ) { if( SEARCH == cursor.key ) SUCCESS ; if( SEARCH > cursor.key ) cursor = cursor.right ; else cursor = cursor.left ; } // search for SEARCH July 2, 2015 IAT 265 15

16. Delete July 2, 2015 IAT 265 16

17. Iterate (In Order) public void inOrder (BNode cursor) { if (cursor == null) return; inOrder(cursor.left ); System.out.println(cursor.key ); inOrder(cursor.right ); } July 2, 2015 IAT 265 17

18. Things arent perfect Unbalanced trees cause slower searches Balancing algorithms manage that Inserting items in order can cause this problem July 2, 2015 IAT 265 18

19. Trees in Java Use the TreeSet class to get this functionality You don t have to build the structure yourself Stores Objects TreeSet t1 = new TreeSet(); t1.add( aaa ); Iterator it1 = t1.iterator(); while( it1.hasNext() ) { Object o1 =it1.next(); System.out.println( o1 ); } July 2, 2015 IAT 265 19