Insights into Fuel Jet Stability and Dynamics

Explore the complex realm of fuel jet stability and dynamics, including topics such as Kelvin-Helmholtz instability, liquid breakup postulations, geometric features of fuel sprays, penetration of spray into air, and more. Gain a deeper understanding of fuel drop formation, spray parameters, structure of gasoline fuel sprays, and the distribution of droplets in different conditions.

• Fuel Jets
• Dynamics
• Stability
• Liquid Breakup
• Spray Parameters

isrossa Follow

Uploaded on Sep 12, 2024 | 2 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

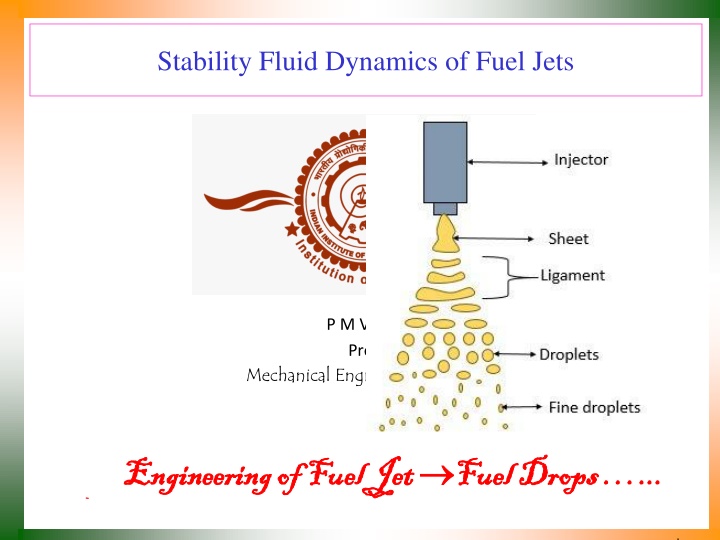
1. Stability Fluid Dynamics of Fuel Jets P M V Subbarao Professor Mechanical Engineering Department Engineering of Fuel Jet Engineering of Fuel Jet Fuel Drops ... Fuel Drops ...

2. Kelvin-Helm Holtz Instability of Micro Fuel Jet Two non-dimensional numbers, namely Reynolds number (Re) and Weber number (We) are identified for the fuel jet. The growth rate ( )and the corresponding wavelength are estimated using these non-dimensional parameters.

3. Postulations for Liquid breakup New drops of radius, r, are formed from bulk liquid or blobs, with characteristic radius Rj. ? = ?? < ?? 0.33 0.33 2?? 2 3??? 2 3??? ? = min , > ?? 4

4. Geometrical Features of A Successful Fuel Spray The angle of spray that leads to formation of droplets described by the angle . ? 2 = 0.118 ??? ????

5. Penetration of Spray into Air Medium 0.25 ???? ???? ???? ???? ???= 2.2 ???????? ? 0.25 ???? ???? ???? ???? ???= 2.2 ???????? ? 0.22

6. Basic Details of Spray for Port Injection Spray/jet parameters: ? 2 = 0.118 ??? ???? ???? ???? ????? ????= ?? 2 0.25 ???? ???? ???? ???? ???= 2.2 ???????? ? ?????= ?????????? 2????????? ????

7. Structure of Gasoline Fuel Sprays in Ports Average drop dia=90 m Average drop dia=70 m Average drop dia=50 m

8. Mean diameter distribution of droplets in 100 mm downstream and 300 Kpa, 25o C

9. Distribution of droplets velocity (m/s) in 100 mm downstream and 300 Kpa, 25o C

10. Frequency diagram for Size of droplets D is the droplet diameter and N is the normalized number distribution.

11. Selection of Statistical Method to Define Average Diameter of Droplet Number distribution function: For same total number of droplets: ? ????= ?=1 ???? ?? ? 3 3 ?=1 ???? ?? ????= ? ? ?=1 ?=1

12. The True Engineering Mean Diameter This diameter is named after the German scientist who first employed it in 1920. Dr Ing J. Sauter worked at the Laboratorium f r Technische Physik of the Technische Hochschule, M chen on aspects of internal combustion engines. In particular, he studied atomization in carburettors and as part of his work devised a technique to determine the size of drops produced based on the absorption/scattering of light. The true mean diameter must have the same ratio of volume to surface area as the entire ensemble. This is known as the Sauter mean diameter or D32.

13. Sauter Mean Diameter ???? = ?=1 ?=1 Introducing the definition of SMD: ? 3 ???? ???? ? 2 The value of SMD found to be a function of on Reynolds number and Weber number of the spray: ?32 Re?? ?? Re?????=????????????????? 2 ??????=?????????? ??????? ????? ????? 0.54????? 0.18 ?32= 4.12???????Re0.12?? 0.75????? ???? ???? where dnozzis the nozzle diameter, f , gare the fuel and gas dynamic viscosity, respectively,

14. Selection of Nozzle diameter & Flow Rate dnozz(mm) Lnozz/dnozz SMD (micrometers) 0.12 1.75 8.45 25.8 61.3 124.3 226.2 9 SMD(micrometers ) 0.1 0.2 0.3 0.4 0.5 0.6 0.7 36.1 18.05 12.0 9.0 7.22 6.02 5.16 Injection rate (kg/hr) 5 128.389 7 80.6993 57.0493 11 43.2497 13 34.345

15. Need for Theory of Pulsating Fuel Flow 1.0 . . . . -360 Crank angle in degrees -270 -90 -180 50 -45 0 -450 The pressure gradient across the injector openings can be defined as a trapezoidal pulse train. This pulse train in real time is mapped as a Fourier series with non- dimensional time and frequency as governing parameters. ? ?,? = ? ? + ??,?? ??? 2???? + ??,?? ??? 2???? ?=1 ?=1 ??? ?2????? ? ?,? = ? ? + ?=1

16. New Chapter in Fluid Mechanics Fully developed axisymmetric pulsating laminar pipe flow. The Navier-Stokes equation for an axisymmetric flow can be written as: U t P x U r = + r r r The pressure gradient in the above equation can be written in the form of a Fourier transform as discussed above. ? ?,? =? ? ? ? ??? ?? ?2????? + ?? ?=1 The equation when solved gives absolute flow velocity and mass flow rate mapped against time in a complex space: ( ) = 1/23/2 i P R r R U 2 /8 J 2 F r ( ) P nF 4 U U 0 ( ) m ave = = nF i 2 U en 2 1 r 1 exp 2 ( ) = 1/23/2 i J 2 F r / = n 1 m 0

17. Instantaneous Mass Flow Rate The mass flow rate can then be solved for: ( ) 1/2 1/2 3/2 2 i J 2 nF i P i nF 4 m m 1 ( ) = = + nF i m en 1 1 exp 2 ( ) ( ) 1/2 1/23/2 i 2 nF J 2 nF = n 1 m 0 The non-dimensional frequency and time are given as below = m 2 R U m m = 2 F R f / t R = 2 / R is the radius of the nozzle tip.

18. Anatomy of Modern Injectors to generate Pulsating Fuel Flow Jets Solenoid Magnet