Graphs of Equations and Functions Overview
The basics of graphing equations and functions on the coordinate plane. Learn about quadrants, labeling points, linear equations, and graphing techniques. Dive into real-life scenarios to understand the practical applications of linear functions and how to interpret them graphically. Master the art of graphing linear equations and use them to make predictions in scenarios involving costs, debts, and more.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
ALGEBRA UNIT 4: GRAPHS OF EQUATIONS AND FUNCTIONS Unit 4 PowerPoint
THE COORDINATE PLANE REVIEW Overview 4 quadrants Labeled with x and y axis X axis is horizontal Y axis is vertical Labeled with coordinates (x, y)
LABELING POINTS Label the points (4, 3) (-1, 0) (-2, - 3) (2, - 3)
HIDDEN MESSAGE ACTIVITY Complete the coordinate plane activity to reveal the secret message.
GENERAL GRAPH OF A LINEAR FUNCTION When you hear linear, what do you think of? What do you think a linear function will look like?
GRAPHING A LINEAR EQUATION A taxi fare costs more the further you travel. Taxi s charge a fee on top of the per-mile charge to cover hire of the vehicle. For our example, the taxi charges a set fee of $3, plus $.80 per mile traveled. Write an equation and graph the solutions.
GRAPHING A LINEAR EQUATION Equation: y = $3.00 + $.80x Where y is total cost and x is miles traveled. Graph: 1- make a t-chart 2- pick x- values to plug in 3- calculate the y- values 4- plot the points 5- draw the line
GRAPHING A LINEAR EQUATION A small business has a debt of $500,000 incurred from start-up costs. It predicts that it can pay off the debt at a rate of $85,000 per year according to the equation governing years in business (X) and debt measure in thousands of dollars (y). Y = -85x + 500 Graph the equation and use the graph to predict when the debt will be fully paid.
GRAPHING A LINEAR EQUATION Graph: Y = 3x + 2 Y = - 4x + 5 Y = .5x 1.5
GRAPHS OF HORIZONTAL AND VERTICAL LINES How would you graph the two following lines? Y = 3 X = - 4
HORIZONTAL AND VERTICAL LINES Mad-cabs have an unusual offer going on. They are charging $7.50 for a taxi ride of any length within the city limits. Graph the function that relates the cost of hiring the taxi (y) to the length of the journey in miles (x).
USING AND INTERPRETING LINEAR GRAPHS Use the graph to convert: 70 F to C 0 F to C 30 C to F 0 C to F
ACTIVITY Grab a laptop and go to this website: http://www.mathplayground.com/SaveTheZogs/SaveTheZogs.htm l You are going to save the zogs using your equation tools. See what level you can get too.
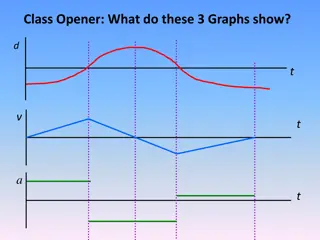
WHAT IS A LINEAR FUNCTION? How many times will the line cross the x-axis? What about the y-axis?
X- AND Y- INTERCEPTS X-intercept: where the line touches/crosses the x axis (where the y value will be zero.) Y-intercept: where the line touches/crosses the y axis (where the x value will be zero.)
SLOPE-INTERCEPT FORM OF AN EQUATION Y = mx + b Where x and y are your coordinate points M is your slope B is your y-intercept (where the line touches the y-axis)
SLOPE-INTERCEPT FORM What is the slope, what is the y-intercept? Y = 5x + 3 Y = -12x 4 Y = x + 1.5
SLOPE- INTERCEPT FORM To find slope: calculate the rise and run of a line
FINDING SLOPE FROM A GRAPH Find the rise and the run, then divide the two (Rise / Run) Example:
DETERMINING SLOPE GIVEN TWO POINTS ON A LINE Given two points (x1, y1) and (x2, y2) ?2 ?1 ?2 ?1 ????? =
FINDING SLOPE GIVEN TWO POINTS Given the points: (19, -16) and (-7, -15) (-4, 7) and (-6, -4)
WHAT IS THE IMPORTANCE? What would be the importance of the y- intercept in the example below: A taxi fare costs more the further you travel. Taxi s charge a fee on top of the per-mile charge to cover hire of the vehicle. For our example, the taxi charges a set fee of $3, plus $.80 per mile traveled. Write an equation and graph the solutions.
WHAT IS THE IMPORTANCE? Farmer Ali had a well on his property 200 feet deep. When the well went dry, he hired a company to drill the well deeper. He used the equation d= -75t 200 to find the depth of the well, d, using the number of days the company drilled, t. What is the slope of the line? What does the slope represent in the context of the problem?
WHAT IS THE IMPORTANCE? Pierce the plumber charges $25 for a service call. He uses the equation C = 50h + 25 to determine the charge of his services, C, after working h hours. What is the slope of the line? What does the slope represent in the context of the problem? What is the y-intercept of the line? What does the y-intercept represent in the context of the problem?
FINDING INTERCEPTS IN SLOPE INTERCEPT FORM To find intercepts in slope intercept form: Plug in 0 for x to find the y-intercept Plug in 0 for y to find the x-intercept
GRAPHING INTERCEPTS IN SLOPE INTERCEPT FORM Once you have determined the intercepts of the graph, plot them and draw a line between the two.
EXAMPLE Y = 2x 3
FINDING INTERCEPTS IN STANDARD FORM To find intercepts in standard form, Plug in 0 for x to find the y-intercept Plug in 0 for y to find the x-intercept
GRAPHING INTERCEPTS IN STANDARD FORM Once you have determine the intercepts of the graph, plot them and draw a line between the two.
EXAMPLE 4x 3y = 12