Features of x^3 Graphs and Tangents Analysis

Investigate the key features of x^3 graphs, including the stationary points, slope function characteristics, and tangent behavior. Understand the relationship between the original function f(x) and its derivative dy/dx. Explore where slopes are increasing, decreasing, or stationary, along with the turning points and inflection points. Learn how to interpret the slope function graph and determine when the slopes transition from decreasing to increasing. Discover insights on the position of the slope function relative to the x-axis and the shapes of the graphs involved.

• Graph analysis
• Tangents
• Derivatives
• Stationary points
• Slope function

brandl_d Follow

Uploaded on Feb 26, 2025 | 0 Views

Download Presentation

Please find below an Image/Link to download the presentation.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.

You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.

The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.

Presentation Transcript

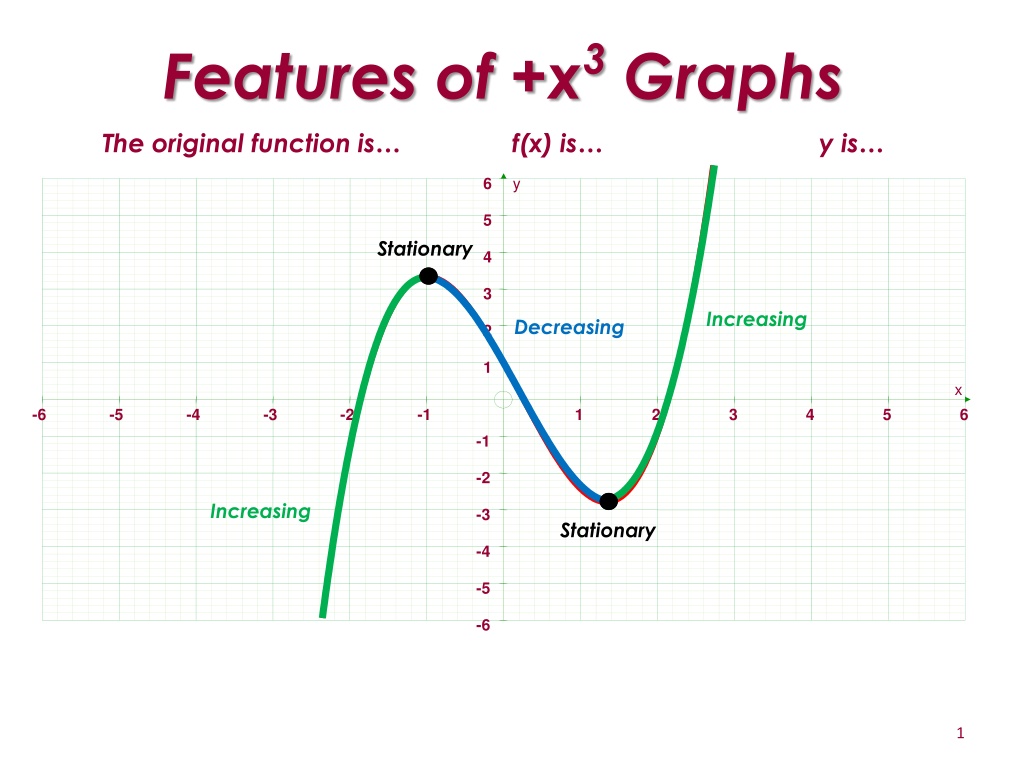
1. Features of +x3 Graphs The original function is f(x) is y is y 6 5 Stationary 4 3 Increasing Decreasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 Increasing -3 Stationary -4 -5 -6 1

2. Investigate the tangents of +x3 Graphs The slope function is f (x) is dy/dx is y 6 5 4 3 Slope values are decreasing 2 1 x -6 -5 -4 -3 -2 -1 Point of Inflection = slopes stop decreasing and start increasing 1 2 3 4 5 6 -1 Slope values are increasing -2 -3 -4 -5 -6 2

3. Features of the Slope Function Graph Reading the features of the graph of the slope function from the original function y 6 Turning Point of the slope function: where slopes turn from decreasing to increasing = min 5 slope function = 0 (cuts x-axis) dy/dx= 0 4 3 2 Slope values are increasing slope function increasing Slope values are decreasing slope function 1 x -6 -5 -4 decreasing -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 dy/dx= 0 slope function = 0 (cuts x-axis) -4 -5 -6 Slope Function: U shaped (positive cubic graph will have positive derivative graph) Minimum point at same x value as the point of inflection Cuts x-axis at the x values of the turning points 3

4. The slope function is f (x) is dy/dx is y 6 ORIGINAL FUNCTION y = f(x) 5 dy/dx= 0; slope function = 0 4 Turning Point: Decreasing to increasing = min pt 3 Slope values are decreasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 Slope values are increasing -2 -3 dy/dx= 0; slope function = 0 -4 -5 -6 y 6 SLOPE FUNCTION y = f (x) 5 4 3 Slope values are increasing Slope values are decreasing 2 1 x x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 dy/dx= 0; slope function = 0 -1 dy/dx= 0; slope function = 0 -2 Turning Point: Decreasing to -3 increasing -4 = min pt -5 4 -6

5. Also, we can read where the slope function is above and below the x-axis from the original function + + + + + + + 0 - - - - - - - - - - 0 + + + + + + + y 6 5 4 3 Slopes are negative Slopes are positive Slopes are positive 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6 6 y 5 4 Slope Function above x-axis Slope Function above x-axis 3 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 Slope Function below x-axis -3 -4 -5 5 -6

6. At what rate is the slope function changing? f(x) is d2y/dx2 is... y 6 5 How fast is the rate of decrease of the slopes? 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 How fast is the rate of increase of the slopes? -1 -2 -3 -4 -5 -6 Finding the rate of change of the rate of change . Finding the second derivative 6

7. A step further to investigate the tangents of the slope function. Second Derivative Function is f (x) is d2y/dx2 is... y 6 ORIGNAL FUNCTION y = f(x) 5 dy/dx= 0; slope function = 0 4 Turning Point: Decreasing to increasing = min pt 3 Slope values are decreasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 Slope values are increasing -2 -3 dy/dx= 0; slope function = 0 -4 -5 -6 y 6 SLOPE FUNCTION y = f (x) 5 4 3 Slope values are decreasing Slope values are increasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 dy/dx= 0; slope function = 0 dy/dx= 0; slope function = 0 -1 -2 Turning Point: Decreasing to -3 -4 increasing = min pt -5 7 -6

8. y 6 SLOPE FUNCTION y = f (x) 5 4 3 Slope values are decreasing Slope values are increasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 dy/dx= 0; slope function = 0 dy/dx= 0; slope function = 0 -1 -2 Turning Point: Decreasing to -3 -4 increasing = min pt -5 -6

9. y 6 SLOPE FUNCTION y = f (x) 5 4 3 Slope values are increasing Second Derivative Function is increasing Slope values are increasing Second Derivative Function is increasing 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 Slope=0 (d2y/dx2 = 0) Second Derivative Function =0 -3 -4 -5 (cuts x-axis) -6 y 6 5 SECOND DERIVATIVE FUNCTION y = f (x) 4 3 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6

10. Original Function, First Derivative Function, Second Derivative Function y 6 5 4 3 y = f(x) 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6 y 6 5 4 3 y = f (x) 2 1 x -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 ??????? ?????? ?? ???????? ???????? ?? ?? ??= ? -1 -2 -3 -4 -5 -6 6 y 5 ????? ??? =??? ???> ? 4 3 y = f (x) 2 1 x -6 -5 ????? ??? =??? ???< ? -4 -3 -2 -1 1 2 3 4 5 6 -1 -2 -3 -4 -5 -6 10