Exploring Heron's Formula in Mathematics

STD IX MATHEMATICS TOPIC- HERON S FORMULA Work is Worship

PDF CHAPTER LINK Herons Formula(ncert).pdf Unit 12(Exemplar Heron's Formula).pdf Work is Worship

Learning Objectives Students will be able to recall the formula for finding area and perimeter of closed geometrical figure . know the formula for finding area of a scalene triangle . Application of Heron s formula in finding area of quadrilateral . verify that Heron s formula is also applicable for other triangles. estimate the area of different shapes of geometrical figures . Work is Worship

Why will we study Herons Formula ? To find area of cloth required for an umbrella To find the area of tiles required for the floor To find the area of a triangular shaped pizza . Work is Worship

INTRODUCTION In earlier classes , we have studied areas of some plane figures such as rectangle , square , perimeter , right angled triangle , quadrilateral , etc. The length of the boundary of a closed figure is called the perimeter of the plane figure . A part of the plane enclosed by a simple closed figure is called plane region and the measurement of the plane region is called its area . Area is usually measured in square meter (m2) or square centimeter (cm2) . Work is Worship

REVIEW OF SOME IMPORTANT FORMULAE RECTANGLE : Perimeter = 2(l+b) Area = l X b SQUARE : Perimeter = 4 X side = 4a Area = side x side = a2 TRAPEZIUM: area = X h x (a+b) RHOMBUS : Area = x d1x d2 b l a a a a a h d1 d2 b Work is Worship

TRIANGLE A 1. SCALENE TRIANGLE Perimeter = a+b+c Area = x a x h 2. EQUILATERAL TRIANGLE : Area = a2 Height = 3. RIGHT ANGLED TRIANGLE : Area = x a x b c b h B C a A a a h A C B a b B a C Work is Worship

some useful conversions for area 1m2 = 1m x 1m = 100cm x 100cm = 10000cm2 1dm2 = 1dm x 1dm =10cm x 10cm = 100cm2 1 Hectare = 100m x 100m = 10000m2 Work is Worship

HERONS FORMULA Work is Worship

What is Herons Formula ? The famous formula derived by Heron for the area of a scalene triangle when height is not given is Heron s formula . Work is Worship

ABOUT HERON Work is Worship

a ,b , c are sides of the triangle . Perimeter of the triangle = a + b + c S is semi-perimeter . Work is Worship

PROOF OF HERONS FORMULA Semi-perimeter , s = => s-a = , s-b = , s-c = In right , we have (i) h2= c2 x2 (by Pythagoras theorem ) In right triangle ADC , we have , A h2 = b2 (a-x)2 From equations (I) and (ii) , we get c2 x2 = b2 (a-x)2 on simplification, x = (ii) b c h substituting the value of x in (I) , we get B x a-x h2 = c2 - => h = . area of triangle ABC is = x a x = D C a on simplification, == Work is Worship

VIDEO-HERONS FORMULA VID-20200430-WA0016.mp4 Work is Worship

EXAMPLE Find the area of a triangle whose sides are 8cm and 11cm and 13cm. (2marks) Sol. Perimeter = 8+13+11=32cm a = 8cm b =11cm. c = 13cm. s(semi-perimeter) = 32 2 =16 cm ( mark) Area = (1/2 mark) = = = 8 cm2 (1 mark) A 13cm 11cm C B 8cm Work is Worship

EXAMPLE 1.Calculate the area of the shaded region in the given figure. (4marks) Sol. S (semi-perimeter) = ???+???+?? ? Area of the bigger triangle = ? ? ? ? ? (? ?) = 132m. ? ? = ??? ??? ??? ??? ??? (??? ??) = ??? ?? ?? (???) = 1320???? 122m 120m ? Area of the smaller triangle S = ??+??+?? ? Area = ? ? ? ? ? (? ?) = 36 1 2 26m 24m = ?? ?? ?? ?? ?? (?? ??) = ??????????? = 24 ?????= 24X10.25?? = 246???? 22m ? Area of the shaded region = area of the bigger triangle Area of the smaller triangle = 1320-246 = 1074?? 1 Work is Worship

REMARK Heron sformula was derived specially for scalene triangles . But it is applicable to all type of triangles . Work is Worship

QUESTIONS 1.The perimeter of an equilateral triangle is 60cm .The area is (a) 10 ?c?? (b) 15 ?c?? (c) 20 ?c?? (d)100 ?c?? Ans- 100 ?c?? (1 mark) 2.The area of an isosceles triangle having base 2cm and the length of one of the equal sides is 4cm . Find the area of the triangle. Sol. Area of the triangle = ? ?mark) = ? ?mark) ? ???? ?? (? ? X 2 ?? = ??c?? (? Work is Worship

APPLICATION OF HERONS FORMULA IN FINDING AREAS OF QUADRILATERALS Work is Worship

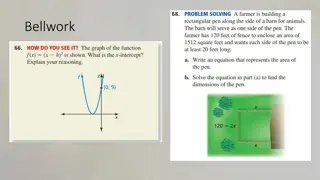
QUESTION A park is in the shape of quadrilateral ABCD . Given that angle C=90 Also AB=9 m, BC=12 m, CD=5 m and AD=8 m. How much area does it occupy? (4mark) Work is Worship

Sol. 9cm B A 12cm 8cm D C 5cm BCD, using Pythagoras theorem, Sol. In B??=B??+C??(1/2 mark) BD= ??? + ??= ???=13m Therefore, Area of BCD=? Now, In ABD, Semi-perimeter (s)=??+?+?? ? =15m (1/2 mark) Area of ABD= ?(? ?)(? ?)(? ?) Area of ABD= ??(?? ?)(?? ?)(?? ??) (1mark) Area of ABD= ?? ? ? ?=? ???? Therefore, Area of quadrilateral ABCD= Area of Therefore, Area of quadrilateral ABCD=30+6 ?? = 65.5?? (1 mark) ? 12 5=30?? (1mark) ABD+ Area of BCD Work is Worship

QUESTION A kite in the shape of a square with a diagonal 32 cm and an isosceles triangles of base 8 cm and sides 6 cm each is to be made of three different shades as shown in the given figure. How much paper of each shade has been used in it? (3 mark) Work is Worship

A Sol. Each diagonal of the square = 32cm AO = ? ? X 32 = 16cm ( mark) I Area of each of shades I and II X base X height = X 32 X 16 =256c?? And area of shade III with sides 6cm,6cm and 8cm (1mark) = ? B o D II ? ? ???? ????? ? ??? ??= = 2 X ??? ????? = 2 x ?????= ? ???? (1 mark) = 1792C?? C 6cm III 8cm Work is Worship

1. Student will be asked to cut eight equal triangles of given sides by using two different colours . 2. They will paste the triangular papers to make the above floral design. 3. They will find area of different color papers used by them Work is Worship

HERONS FORMULA Heron s formula Right angled triangle Equilateral triangle = = Application = X b X h Where a , b , c are the length of the sides a a h b a s = semi perimeter = a = side of the triangle Base= b, height = h Find area of a triangle of side 122cm, 22cm, 120cm. By Herons formula: Area of Quadrilateral ABCD = Area of ABC + Area of ACD D = A Where s = Area of ABC= X 12 X 5=30m2. 9cm 12cm = 132. = = C B = 5cm Area= = 1320cm2. = 35.496 = = 15m. Where s = = = Work is Worship

THANK YOU Work is Worship