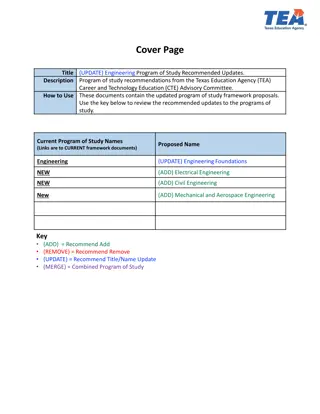
Exploring Engineering Mathematics and Automata Theory Concepts
Delve into topics such as automata theory, Turing machines, and mathematical approaches for addition using unary numbers. Discover state transition diagrams and gain insights into the workings of Turing machines in computer science.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
18mat31 18mat31 Module 1 Module 1 Engineering Mathematics - III MANOHAR KUMAR K.N MANOHAR KUMAR K.N Assistant Professor Department of Mathematics K.S. School of Engineering and Management Bengaluru - 560109
Automata Automata theory theory and 17CS54 17CS54 and Computability Computability Module 1 Module 1 . Turing Machine as an Adder Mr. Sandeep H Associate Professor Department of CSE K.S. School of Engineering and Management Bengaluru - 560109
Approach for Addition 1. Numbers are given in Unary form 2. Example: 3 = 111, 2 = 11, 5 = 11111 etc. 3. For addition of 3 and 4, numbers will be given in TAPE as "B B 1 1 1 0 1 1 1 1 B B". 4. Convert '0' to '1' and reduce '1' from right 5. Hence output will be "B B 1 1 1 1 1 1 1 B B B" 6. Total number of '1' in output is = 7 which is addition of 3 and 4
Explanation of TAPE movement 1. Input is given as "11011" (2 + 2) 2. Scan string from left to right 3. Pass all '1 s and convert '0' to '1' 4. Reach BLANK in right 5. Convert rightmost '1' to BLANK and move Left Addition of 2 and 2 = 4 is written on TAPE Input String : 11011 Output String : 1111
State Transition Diagram We have designed state transition diagram for adder as follows: Start scanning string from left to right Pass all '1's and keep moving right Convert '0' to '1' and keep moving right When BLANK(in right) is reached move one step left convert '1' to BLANK Keep moving left after that to point start of string Number of '1's is reduced because number of '1' was increased by one while converting '0' to '1'
Turing machine for function = + ( , ) f x y x y 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 8
Execution Example: Time 0 y x = 11 x (=2) 1 1 0 1 1 = 11 y (=2) q 0 Final Result x+ y 0 1 1 1 1 q 4 9
1 1 0 1 1 Time 0 q 0 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 10
1 1 0 1 1 Time 1 q 0 1 , 1 R 1 1 , 1 , 1 R L , 0 1 , L L , 1 R q q 1 q q 2 0 3 , R q 4 11
1 1 0 1 1 Time 2 q 0 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 12
1 1 1 1 1 Time 3 1 q 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 13
1 1 1 1 1 Time 4 1 q 1 , 1 R 1 1 , 1 , 1 R L , 0 1 , L L , 1 R q q 1 q q 2 0 3 , R q 4 14
1 1 1 1 1 Time 5 1 q 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 15
1 1 1 1 1 Time 6 q 2 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L L , 1 R q q 1 q q 2 0 3 , R q 4 16
1 1 1 1 Time 7 q 3 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 17
1 1 1 1 Time 8 q 3 1 , 1 R 1 1 , 1 , 1 R L , 0 1 , L L , 1 R q q 1 q q 2 0 3 , R q 4 18
1 1 1 1 Time 9 q 3 1 , 1 R 1 1 , 1 , 1 R L , 0 1 , L L , 1 R q q 1 q q 2 0 3 , R q 4 19
1 1 1 1 Time 10 q 3 1 , 1 R 1 1 , 1 , 1 L R 1 , L , 0 L , 1 R q q 1 q q 2 0 3 , R q 4 20
1 1 1 1 Time 11 q 3 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q 4 21
1 1 1 1 Time 12 q 4 1 , 1 R 1 1 , 1 , 1 L R , 0 1 , L , 1 L R q q 1 q q 2 0 3 , R q HALT & Accept 4 22