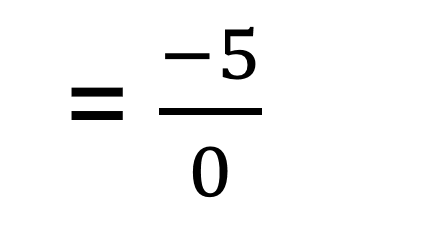Equations of Lines: Standard Form and Slopes
Warm Up
Write the
Standard Form
equation of
the line that passes through the points (5, 2)
and (5, –3).
x – 5 = 0
x = 5
undefined
Parallel & Perpendicular Lines
Parallel Lines
-
coplanar lines that do not
intersect
-
have the same slope and different
y-intercepts
Perpendicular Lines
-
intersect to form 4 right angles
-
slopes are the opposite sign and
reciprocal of one another
Find the slope of each line. Then determine whether the
lines are parallel, perpendicular, or neither…
1. y = 3x – 2
2. y = 8x – 1
x + 3y = –9 7x – y – 1 = 0
Perpendicular Lines
Neither
m = 3
3y = –x – 9
m = 8
–y = –7x + 1
y = 7x – 1
m = 7
3. y = x – 9
4. y = 2x + 4
x – y + 9 = 0
x + 2y + 10 = 0
Perpendicular Lines
Parallel Lines
Find the slope of each line. Then determine whether
the lines are parallel, perpendicular, or neither…
m = 1
–y = –x – 9
y = x + 9
m = 1
m = 2
2y = –x – 10
5. Write the standard form equation of the
line that passes through
(2, –3)
and is
parallel to the line…
4x – y + 3 = 0
4x – y – 11 = 0
m = 4
–y = –4x – 3
y = 4x + 3
m = 4, (2, –3)
y – (–3) = 4(x – 2)
y + 3 = 4(x – 2)
y + 3 = 4x – 8
6. Write the standard form equation of the line that
passes through
(3, –5)
and is perpendicular to
the line…
2x – 3y + 6 = 0
3x + 2y + 1 = 0
–3y = –2x – 6
2y + 10 = –3x + 9
7. a. Write the standard form equation of
the line that passes through
(2, 3)
and is
parallel to the line…
y – 5 = 0
b. What is the equation of the line that
is perpendicular ?
m = 0
m = 0
y – 3 = 0
m = 0
m = undefined
x = 2
x – 2 = 0
y = 3
8. a. Write the standard form equation
of the line that passes through
(–1, 4)
and is parallel to the line…
x + 3 = 0
b. What is the equation of the line
that is perpendicular ?
m = undefined
m = undefined
x + 1 = 0
m = 0
m = undefined
y – 4 = 0
y = 4
x = –1
9. For what value of k is the graph of
kx – 7y + 10 = 0
parallel to the graph of
8x
– 14y + 3 = 0
? For what value of k are the
graphs perpendicular?
–14y = –8x – 3
–7y = –kx – 10
8x – 14y + 3 = 0
kx – 7y + 10 = 0
parallel
k = 4
perpendicular
4k = –49
10. For what value of k is the graph of
2x – ky + 5 = 0
parallel to the graph of
3x + 7y + 15 = 0
? For what value of k are
the graphs perpendicular?
7y = –3x – 15
–ky = –2x – 5
3x + 7y + 15 = 0
2x – ky + 5 = 0
parallel
perpendicular
–3k = 14
7k = 6
Understand how to determine the standard form equation of a line passing through given points, identify whether lines are parallel or perpendicular based on their slopes, and solve problems involving parallel and perpendicular lines.
Download Presentation
Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author. Download presentation by click this link. If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
E N D
Presentation Transcript
Warm Up Write the Standard Form equation of the line that passes through the points (5, 2) and (5, 3). m = ?2 ?1 ?2 ?1 = 3 2 5 5 x = 5 = 5 x 5 = 0 undefined 0
Parallel & Perpendicular Lines Parallel Lines - coplanar lines that do not intersect - have the same slope and different y-intercepts Perpendicular Lines - intersect to form 4 right angles - slopes are the opposite sign and reciprocal of one another
Find the slope of each line. Then determine whether the lines are parallel, perpendicular, or neither 1. y = 3x 2 2. y = 8x 1 x + 3y = 9 7x y 1 = 0 y = 7x + 1 3y = x 9 y = 7x 1 y = 1 3x 3 m = 1 m = 8 m = 7 m = 3 3 Perpendicular Lines Neither
Find the slope of each line. Then determine whether the lines are parallel, perpendicular, or neither 3. y = x 9 x y + 9 = 0 4. y = 2x + 4 x + 2y + 10 = 0 2y = x 10 y = x 9 y = x + 9 y = 1 2x 5 m = 1 m = 1 m = 1 m = 2 2 Perpendicular Lines Parallel Lines
5. Write the standard form equation of the line that passes through (2, 3) and is parallel to the line 4x y + 3 = 0 y = 4x 3 m = 4, (2, 3) y ?1 = m(x ?1) y ( 3) = 4(x 2) y + 3 = 4(x 2) y = 4x + 3 m = 4 y + 3 = 4x 8 4x y 11 = 0
6. Write the standard form equation of the line that passes through (3, 5) and is perpendicular to the line 2x 3y + 6 = 0 m = 3 3y = 2x 6 2, (3, 5) y = 2 y ?1 = m(x ?1) 3x + 2 y ( 5) = 3 2(x 3) m = 2 3 y + 5 = 3 2(x 3) 2x + 9 2y + 10 = 3x + 9 y + 5 = 3 3x + 2y + 1 = 0 2
7. a. Write the standard form equation of the line that passes through (2, 3) and is parallel to the line y 5 = 0 m = 0 m = 0 y 3 = 0 y = 3 b. What is the equation of the line that is perpendicular ? x = 2 m = 0 x 2 = 0 m = undefined
8. a. Write the standard form equation of the line that passes through ( 1, 4) and is parallel to the line x + 3 = 0 m = undefined x = 1 x + 1 = 0 m = undefined b. What is the equation of the line that is perpendicular ? m = undefined y = 4 y 4 = 0 m = 0
9. For what value of k is the graph of kx 7y + 10 = 0 parallel to the graph of 8x 14y + 3 = 0? For what value of k are the graphs perpendicular? kx 7y + 10 = 0 parallel 8x 14y + 3 = 0 ? 7 = 4 7y = kx 10 14y = 8x 3 y = 8 7 y = ? 7x + 10 m = ? 7 k = 4 14x + 3 7 14 perpendicular y = 4 7x + 3 4k = 49 ? 7 = 7 14 k = 49 4 m = 4 4 7
10. For what value of k is the graph of 2x ky + 5 = 0 parallel to the graph of 3x + 7y + 15 = 0? For what value of k are the graphs perpendicular? 2x ky + 5 = 0 parallel 3k = 14 3x + 7y + 15 = 0 2 ? = 3 ky = 2x 5 7 7y = 3x 15 y = 3 y = 2 ?x + 5 k = 14 7x 15 ? 3 7 perpendicular m = 2 m = 3 ? 7k = 6 2 ? = 7 7 3 k = 6 7
