Depth-First Search in Graph Algorithms
Delve into the world of graph algorithms and explore Depth-First Search (DFS) in both undirected and directed graphs. Learn about tree edges, back edges, forward edges, and cross edges, along with the terminology associated with DFS trees. Discover how to detect back edges and perform a depth-first search efficiently. Enhance your understanding of graph traversal and edge classification in a structured manner.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Convex Hull Questions? CS 4412 Graph Algorithms 2
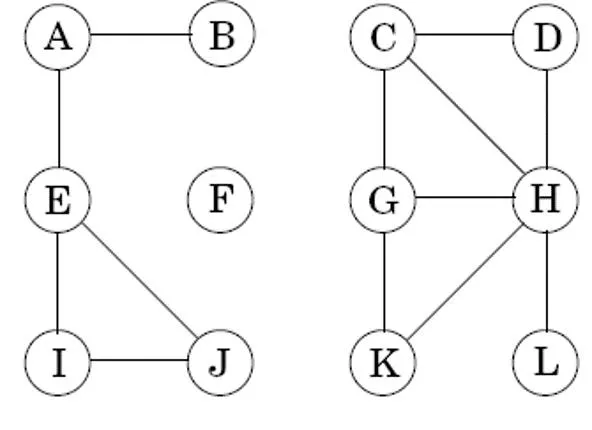
Review: DFS in undirected graphs CS 4412 Graph Algorithms 3
Depth-First Search in Directed Graphs Can use the same DFS algorithm as before, but only traverse edges in the prescribed direction Thus, each edge just considered once (not twice like undirected) still can have separate edges in both directions (e.g., if we had (e, b)) Root node of DFS tree is A in this case (if we go alphabetically), Other nodes are descendants of A in the DFS tree Natural definitions for ancestor, parent, child in the DFS Tree CS 4412 Graph Algorithms 4
A 1,16 Let's do it B C 2,11 12,15 E D 3,10 13,14 F H 8,9 4,7 G 5,6 CS 4412 Graph Algorithms 5
Depth-First Search in Directed Graphs Tree edges and back edges (2 below) the same as before Added terminology for DFS Tree of a directed graph Forward edges lead from a node to a nonchild descendant (2 below) Cross edges lead to neither descendant or ancestor; lead to a node which has already had its postvisit (2 below) CS 4412 Graph Algorithms 6
Back Edge Detection Ancestor/descendant relations, as well as edge types can be read off directly from pre and post numbers of the DFS tree just check nodes connected by each edge Initial node of edge is u and final node is v Tree/forward reads pre(u) < pre(v) < post(v) < post(u) If G First? CS 4412 Graph Algorithms 7
TAPPS Perform depth-first search the graph; whenever there s a choice of vertices, pick the one that is alphabetically first. Classify each edge as a tree edge, forward edge, back edge, or cross edge, and give the pre and post number of each vertex. CS 4412 Graph Algorithms 8
A B E 1,16 17,18 19,20 cross edge H C 2,9 10,15 cross edge G D 3,8 11,14 back edge I F 12,13 4,7 J 5,6 CS 4412 Graph Algorithms 9
DAG Directed Acyclic Graph DAG a directed graph with no cycles Very common in applications Ordering of a set of tasks. Must finish pre-tasks before another task can be done How do we test if a directed graph is acyclic in linear time? Property: A directed graph has a cycle iff DFS reveals a back edge Just do DFS and see if there are any back edges Given the DFS tree, how do we check DFS for back edges and what is complexity? O(|E|) for edge check pre/post values of nodes Could equivalently test while building the DFS tree CS 4412 Graph Algorithms 10
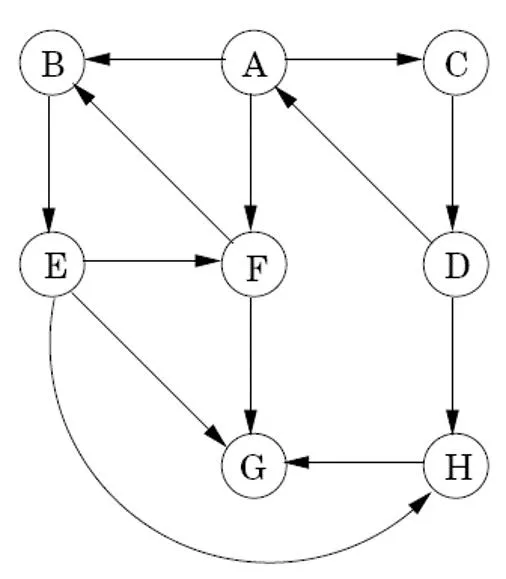
TAPPS Is this graph a DAG? How do you know? CS 4412 Graph Algorithms 11
DAG Properties Linearizations: - B,A,D,C,E,F - B,D,A,C,F,E Every DAG can be linearized: nodes put in sequence so parents always come before children More than one linearization usually possible Algorithm to linearize Property: In a DAG, every edge leads to a node with lower post number Do DFS, then linearize by choosing nodes by decreasing post number Where do we start DFS? Makes no difference, B always has largest post (Try A and F) Another property: Every DAG has at least one source and at least one sink Source has no input edges If multiple sources, linearization can start with any of them Sink has no output edges Is the above directed graph connected? Looks like it if it were undirected (i.e. weakly connected), a DAG is never a strongly connected graph CS 4412 Graph Algorithms 12
TAPPS What are the source and sink nodes in this graph? CS 4412 Graph Algorithms 13
Strongly Connected Components Two nodes u and v in a directed graph are connected if there is a path from u to v and a path from v to u The disjoint subsets of a directed graph which are connected are called strongly connected components Source SCCs and sink SCCs How could we make the entire graph strongly connected? CS 4412 Graph Algorithms 15
Meta-Graphs EVERY directed graph can be represented as a DAG of its strongly connected components This meta-graph decomposition is very useful in many applications (e.g. a high level flow of the task with subtasks abstracted) CS 4412 Graph Algorithms 16
Algorithm to Decompose a Directed Graph into its Strongly Connected Components explore(G,v) terminates precisely when all nodes reachable from v have been visited If we could pick any node v from any sink meta-node and then call explore, it would explore that complete SCC, marking all nodes in it as a SCC, and not reach any other nodes Then remove SCC from the graph (or just use visited flags), and repeat How do we detect if a node is in a meta-sink? How about starting from the node with the lowest post- visit value? Doesn't work with arbitrary graphs (with cycles) which are what we are dealing with. B below could have a lower post order than C even though it is not a sink A B C CS 4412 Graph Algorithms 17
Algorithm to Decompose a Directed Graph into its Strongly Connected Components Property: Node with the highest post in a DFS search must lie in a source SCC Just temporarily reverse the edges in the graph and do a DFS on GR to get post ordering Then node with highest post in DFS of GR, which will be in a source SCC of GR, must be in a sink SCC in G Repeat until graph is empty: Pick node with highest remaining post score (from DFS on GR), explore and mark that SCC in G, and then prune that SCC G GR 18
Example Create GR by reversing graph G Do DFS on GR Repeat until graph G is empty: Pick unvisited node with highest remaining post score (from DFS tree on GR), and explore starting from that node in G, marking each as member of a particular number SCC During the depth-first search, process the vertices in decreasing order of their post numbers That will discover one sink SCC in G Prune all nodes in that SCC from G (or just use the fact that they have been visited) G 3,6 7,10 1,2 8,9 4,5 11,12 GR 13,24 18,19 15,22 14,23 17,20 16,21 CS 4412 Graph Algorithms
TAPPS: Decompose into SCCs Do DFS on GR Repeat until graph G is empty: Pick unvisited node with highest remaining post score (from DFS tree on GR), explore starting from that node in G, marking each as member of a particular number SCC During the DFS, process the vertices in decreasing order of their post numbers That will discover one sink SCC in G Prune all nodes in that SCC from G (or use the fact that they have been visited) Which are source SCCs and which are sink SCCs? Draw the metagraph (each meta-node is an SCC of G). What is the minimum number of edges you must add to this graph to make it strongly connected? CS 4412 Graph Algorithms 20
Solution: Decompose into SCCs Do DFS on GR Repeat until graph G is empty: Pick unvisited node with highest remaining post score (from DFS tree on GR), explore starting from that node in G, marking each as member of a particular number SCC During the DFS, process the vertices in decreasing order of their post numbers That will discover one sink SCC in G Prune all nodes in that SCC from G (or use the fact that they have been visited) Which are source SCCs and which are sink SCCs? Draw the metagraph (each meta-node is an SCC of G). What is the minimum number of edges you must add to this graph to make it strongly connected? CS 4412 Graph Algorithms 21
TAPPS: Complexity We know complexity of DFS is linear - O(|V| + |E|) Is our new algorithm still linear? Only if our new requirements are linear Create GR Order vertices of G by decreasing post values TAPPS: Propose a linear time method for each of these G GR CS 4412 Graph Algorithms
Graph Connectedness Conclusion By doing one linear time, O(|V|+|E|), depth-first search (DFS), we can efficiently gather lots of important information about arbitrary undirected or directed graphs Cycles Connectivity Finding and labeling Connected Components (in directed/undirected graphs) Strongly Connected Components (in directed graphs) Linearizations Finding source and sink nodes and components etc. CS 4412 Graph Algorithms 23