Coupling and Mutual Transformation of Acoustic and Gravitational Modes in Kinematically Complex Flows
This study explores the coupling and mutual transformation of acoustic and gravitational modes in kinematically complex flows. The research delves into phenomena such as stratified fluid, internal gravity waves, and formalism related to background flow and compressible cases. The presentation plan covers the explanation of stratified fluid and internal gravity waves, velocity gradient matrix, wave vector components, and equations for derivatives of velocity components. The work sheds light on the interplay of different modes in complex flow scenarios, offering insights into astrophysics and helioseismology.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
Coupling and mutual transformation of acoustic and gravitational modes in kinematically complex flows. Author: Ia Saralidze Advisor: Andria Rogava Free Univeristy of Tbilisi Reference: Rogava et al. - ACOUSTICS OF KINEMATICALLY COMPLEX SHEAR FLOWS
Presentation Plan 01 02 Phenomenon Explanation Stratified fluid and internal gravity waves 03 Main Formalism Description of background flow 04 Compressible Case Future Perspectives After fluctuation fluid is compressible Astrophysics and helioseismology
01 Phenomenon Explanation Stratified fluid and internal gravity waves
Phenomenon Explanation Stratified fluid density difference between thin layers. Internal gravity waves is created when we have stratified fluid. Internal waves in uniformly stratified fluid visualized by the displacement of dye lines spaced apart by 5 cm. . o
02 Main Formalism Description of background flow
Main Formalism Velocity gradient matrix (shear flow matrix) In the close neighborhood of a point, the spatial variation of the mean velocity can be approximated by a the linear terms in its Taylor expansion. Then a set of nine constants forming the Shear Matrix S: ???,?,? ?0?+ ????? Approximate velocity ??,? ??,? ??,? ??,? ??,? ??,? ??,? ??,? ??,? ?11 ?21 ?31 ?12 ?22 ?32 ?13 ?23 ?33 ? Gradient components
Main Formalism Spatially inhomogeneous operator Velocity gradient ? ??+ ??(?,?,?)?? ???+ ????? Fluctuation function Wave number vector ?(?,?,?;?) ?[? ? ,?]??? ? ??? ?? ?0? ??? ?? Main equation for wave vector K ??? + ?? ? = 0 ?? = ????? ?
Main Formalism ??,?????????? ?? ? ??? ?????? Equations for derivatives of wave vector components (1)= ??? ?2?? ??,?????????? ?? ? ??? ?????? ?? (1)= ?1??+ ??? ?? ??,?????????? ?? ? ??? ?????? (1)= 0 ?? Equations for derivatives of velocity components (1)+ ???+ ?1??= ??? ?? (1) ???+ ?2??= ??? ?? (1)+ ?1??+ ?2??= ??? ??
Main Formalism Equation for derivative of operator D ?(1)= ??? ??+ ??? ??+ ??? ?? Time dependent operator Conserved quantity (1)?? ???? 1= ????? = ??
03 Compressible Case Case where after fluctuation fluid is compressible
Compressible Case Main equations for compressible fluid 2D case ?(1)= ????+ ????+ ????+ ???? (1) ???+ ?2??= ??? ?? Pressure perturbation (1)+ ???+ ?1??= ??? ?? (1)= ??? + ??? ?? Density perturbation ?2= ?? Brunt Vaisala s frequency ? = ??2 ?? + ? ?(1)= ?? Derivative of entropy perturbantion
Compressible Case Deriving main differential equation 2 1(?? ?? ) 2 1(?? + ?? ) 2+ ?? ???? ???? ????+ ????<=> ??= ?? 2+ ?? ??= ?? (1)= (?1 ?2) Quantities we need to find ?1 ?2 ? ??? = ????? ??(1)= ??? ?2? ?(1)= + ???? ?(1)= ?( , ,?) ?(1)= ??
Compressible Case Deriving main differential equation 2+?? (?? 2)(1) 2) 2? +(?? 2 2+?? 2+ ?? (1)= ?? 2) 2+?? (?? ?(1)= ? ??? ? ? ? Main differential equation for coupled system ?(2)+ (?? 2+?2)? = ?? 2? 2+?? (?? 2)1 2) ?(2) (?? 2+2 ?1 ?2 (?? 2)? 2 ????? (?? ?1+ ?? 2+ ?? 2+?? ? = (?? 2+?? 2+?? 2) 2+?? 2)
Compressible Case Removing first order derivative from differential equation 2+?? (?? 2)1 2) ? ? ? => 2?(1) => 2?1 = ? =(?? 1=> ? = 1= ln(?? 2+?? 2) 2+ ?? 2 = 2 ln? ?? 2+?? ? ? 2 2+ ?? 2= ? ?2= ?2+ ?1?2 ?? Final differential equations for coupled system ?(2)+ (?? 2+?2)? = ?? 2? ? 3 ? 2? 2 ????? 2 2+ 2?1 ?2 ? ?? ?(2) 2 2+ ? 2 ?? 2 ?????1 ?2 4? ? = ? 3 ?
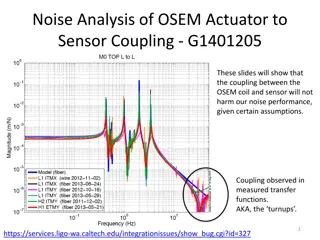
Compressible Case Graphical Representation based on referenced paper
04 Future Perspectives Astrophysics and helioseismology
Thank You Reference: Rogava et al. - ACOUSTICS OF KINEMATICALLY COMPLEX SHEAR FLOWS Author: Ia Saralidze Advisor: Andria Rogava Free Univeristy of Tbilisi
Compressible Case Equation for wave number vector ?2 ?? 2+ ?? 2 (?2)(2)= 4 2?2 2 ?1 ?2 ?(2) ? = 2+ 2 ?4 2?2 ?2 ?1 2 ?(1)= ?2