Advances in Authenticated Garbling for Secure 2PC
The research discusses advancements in authenticated garbling for achieving constant-round malicious secure 2PC using garbled circuits. It emphasizes the utilization of correlated randomness setup and efficient LPN-style assumptions to enhance communication efficiency significantly. Various techniques and security measures, including malicious security for garbled circuits and authenticated garbling from simple correlations, are explored in the context of improving the state of the art in secure 2-party computation.
Download Presentation

Please find below an Image/Link to download the presentation.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.If you encounter any issues during the download, it is possible that the publisher has removed the file from their server.
You are allowed to download the files provided on this website for personal or commercial use, subject to the condition that they are used lawfully. All files are the property of their respective owners.
The content on the website is provided AS IS for your information and personal use only. It may not be sold, licensed, or shared on other websites without obtaining consent from the author.
E N D
Presentation Transcript
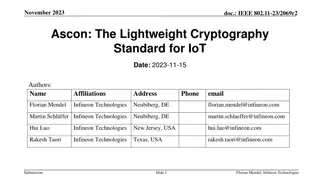
Authenticated Garbling from Simple Correlations Samuel Dittmer Yuval Ishai Steve Lu Rafail Ostrovsky
Our Contribution Goal: constant-round malicious secure 2PC using garbled circuits We obtain significant improvements in communication over the state of the art This relies on simple kinds of correlated randomness setup, generated under LPN-style assumptions. Can be generated with sublinear communication And good concrete efficiency
Authenticated Garbling from Simple Correlations wa Tru th wc wb Ta b le Garbler chooses wire labels La,iand wire mask bits a. Evaluator learns za:= wa aand the corresponding wire label La, z_a (input wires from OT, then from a garbled table). La, z_a Lc, z_c Gar bled Lb, z_b Tab le
Garbling Advances 4 -> 3 Row Reduction [NPS99]: 3 ciphertexts per gate Free XOR [KS08]: 0 ciphertexts per XOR gate Half-Gates [ZRE15]: 2 ciphertexts per AND gate, 0 per XOR Slice and Dice [RR21]: 1.5 ciphertexts per AND gate, 0 per XOR
Malicious Security for Garbled Circuits A malicious garbler can encode the wrong logic into a garbled table. Early advances [MF06, LP07, ] used cut-and-choose techniques to build malicious security with copies of a garbled circuit. Where is a statistical security parameter, typically = 40 [IKOPS11] and [AMPR14] for non-interactive secure computation (NISC) (40x semi-honest).
Authenticated Garbling [WRK17, KRRW18] Constant Round Malicious Secure 2PC OT-based wire authentication Garbled Circuits WRK17 uses Garbled Circuits with free XOR [KS08], and requires 11x cost of semi-honest. KRRW18 uses half-gates [ZRE15] with more efficient OT-based wire authentication, and requires 7.75x cost of semi-honest.
Authenticated Garbling From Simple Correlations More Efficient Malicious 2PC Simple Correlations Garbled Circuits
[Preview] Three Constructions VOLE + MT 1.31x Constant Round Malicious 2PC Semi-honest garbled circuits 2.25x VOLE only 8x Free XOR Half-gates Not yet slice and dice NISC OLE
Road Map Authenticated Garbling Blueprint of Constructions Simple Correlations A Sampling of Techniques
Authenticated Garbling from Simple Correlations x y Truth table Garbled table 0 0 z00= ( a b) c H (La,0, Lb,0, c, 00) (z00, Lc,z_00) 0 1 z01= ( a b) c H (La,0, Lb,1, c, 01) (z01, Lc,z_01) 1 0 z10= ( a b) c H (La,1, Lb,0, c, 10) (z10, Lc,z_10) A malicious garbler A can cheat by using a different truth table. 1 1 z11= ( a b) c H (La,1, Lb,1, c, 11) (z11, Lc,z_11) So A adds a share of a message authentication code (MAC) to zij. But now A can perform a selective failure attack.
Authenticated Garbling from Simple Correlations x y Truth table Garbled table 0 0 z00= ( a b) c H (La,0, Lb,0, c, 00) (z00, Lc,z_00) 0 1 z01= ( a b) c H (La,0, Lb,1, c, 01) (z01, Lc,z_01) 1 0 z10= ( a b) c H (La,1, Lb,0, c, 10) (z10, Lc,z_10) 1 1 z11= ( a b) c H (La,1, Lb,1, c, 11) (z11, Lc,z_11) The values a, b, care generated as secret shares. To authenticate, the parties compute authenticated shares of a, b, c, a b.
Construction: General Blueprint The WRK, KKRW constructions, and each of our three constructions, can be understood as being built up from the following four components: Authenticated Shared Bits Authenticated Parallel And Authenticated Circuit wires Authenticated Garbling
Authenticated Shared Bits wa wc wb Authenticated shares of the mask [ a], i.e. shares of [ a], [ a], [ a], for each wire a, with held by A and held by B.
Authenticated Parallel And wa_1 Authenticated shares of the masks [ a_i], [ b_i], [ c_i] and of the AND gate [ a_i b_i]. wc_1 wb_1 wa_2 wc_2 wb_2 wa_3 Expensive! wc_3 wb_3 wa_4 wc_4 wb_4
Authenticated Circuit Wires wa Authenticated shares of the masks [ s], for all wires s, and of [ s t], for all AND gates (s, t). wc wg wb wd wf we
Authenticated Garbling x y Truth table Garbled table 0 0 z00= ( a b) c H (La,0, Lb,0, c, 00) (s00, Lc,z_00) 0 1 z01= ( a b) c H (La,0, Lb,1, c, 01) (s01, Lc,z_01) 1 0 z10= ( a b) c H (La,1, Lb,0, c, 10) (s10, Lc,z_10) Where sij= [zij]A|| [ zij]Aso B is convinced of the value of zij. 1 z11= ( a b) c H (La,1, Lb,1, c, 11) (s11, Lc,z_11) 1 Or sij= [zij]A, and then B sends zijback to A, who batch-authenticates all zij s.
Authenticated Garbling from Complex Correlations Generate authenticated parallel AND gates (auth. shares of [ a], [ a b]) as correlated randomness: Malicious secure 2PC for a cost 1x semi-honest. Or just generate a garbled circuit! Total communication is o(semi-honest). But we don t know how to do this efficiently.
Authenticated Garbling from Simple Correlations Vector Oblivious Linear Evaluation (VOLE) A holds , B holds v, both parties receive shares of [ v] Many recent protocols for silent and efficient generation using, e.g., LPN assumptions or Silver codes (see e.g. [BCGI18, SGRR19, YWLZW20, CRR21]) Multiplication Triples (MT) Both parties receive shares [x], [y], [z] of vectors x, y, z with xi* yi= zi. Can be generated silently and efficiently using ring-LPN. [BCGIKS20]. A correlation calculus gives variant flavors (VOLE-type and MT-type)
Idea: Authenticated Shared Bits from VOLE wa wc wb Authenticated shares of the mask [ a], i.e. shares of [ a], [ a], [ a], for each wire a, with held by A and held by B. Generate = a b, with a held by A, b held by B. VOLE instances: shares of [ b] and [ a]. We want masks in F2and shares in F2 , so we use a variant: subfield VOLE.
What do we need for Authenticated Parallel AND? ( i j) = (ai bi) (aj bj) = (ai aj) (ai bj) (bi aj) (bi bj) We need authenticated shares of: ai aj ai bj bi bj
Line Point Zero Knowledge [DIO21], [DILO22] Fast designated-verifier zero knowledge using VOLE. Gives a natural tool for verifying relations on entries of VOLE, i.e. a certified VOLE functionality. Now we can share [ (ai aj)] under VOLE. But not [ (ai bj)]
Idea: Block VOLE? Each cross term (ai bj) can be written as ai* bj Treating bjas a constant, we can use VOLE to share [a * bj] and read off all entries [ai* bj]. By our correlation calculus , we can re-use the vector a across multiple instances of VOLE (Good). We call this randomness Block VOLE. But now one VOLE seed per gate (Bad).
Expanding wire labels r11 r12 b*1 1= a1 b1 r1L b*2 2= a2 b2 * r21 r22 r2L 1 * n 2 n= an bn * b*n L rn1 rn2 rnL R = (rij) a public, random matrix L = log n
Idea: Block VOLE! Each cross term (ai b*j) can be written as ai(R *)j, i.e. as a linear combination of terms ai *. We now need only L log n instances of VOLE. Drawback: Many relations now hold on B s wire labels.
Corrupting multiple rows For each vector vTin the co-kernel of R, A knows the linear combination of wire masks vT = vTa + vTR *= vTa. Lemma: every non-zero vTin coker(R) has > nonzero entries w.h.p. If A corrupts > table entries, B will almost always abort. Gar bled Gar bled Tab le Gar bled Tab le Gar bled Tab le Gar bled Tab le Gar bled Tab le Tab le
I have a truly marvelous demonstration of this proposition which this margin is too narrow to contain. [F65] Parallel AND Gates from MT-type randomness and Beaver/SPDZ methods. Parallel AND Gates from Programmable OLE (for NISC). Certification between flavors of randomness. Conditional Disclosure of Secrets (for NISC). Efficient compiler from statistical to computational security (saving on the cost of generating authenticated Parallel AND gates). Mixing and matching garbling techniques (WRK + KRRW) for VOLE-only and NISC constructions to avoid leakage and extra rounds, respectively.
Our Results (Malicious 2PC) Protocol Correlation Cost (Garbled Circuits) Dep. + Online Total WRK OT 2.5 11 KRRW v1 OT 1.5 7.75 KRRW v2 OT 1 9.7 KRRW + VOLE FVOLE 1 2.5 KRRW + SPDZ FMT 1 7 KRRW + SPDZ + Cert. VOLE FMTFsubVOLE FVOLE 1 2.9 Ours, v1 FDAMTFsubVOLE FVOLE 1 1.31 Ours, v2 FbVOLE FsubVOLE FVOLE 1.47 2.25
Our Results (NISC in the single-execution setting) Protocol Correlation Cost (Garbled Circuits) Dep. + Online Total Ours, v3 Programmable FOLE 8 8 AMPR14 CRS 40 40