Advancements in Simple Multigraph Convolution Networks by Xinjie Shen
Explore the latest innovations in simple multigraph convolution networks presented by Xinjie Shen from South China University of Technology. The research evaluates existing methods, such as PGCN, MGCN, and MIMO-GCN, and introduces novel techniques for building credible graphs through subgraph-level
6 views • 6 slides
Privacy-Preserving Analysis of Graph Structures
Explore the world of graph structures and differential privacy in data publishing networks, focusing on preserving privacy while releasing structural information about graphs. Differential privacy techniques such as edge privacy and subgraph counts are discussed in detail, highlighting the challenge
0 views • 20 slides
Recent Applications of Quasi-Poly Time Hardness in Densest k-Subgraph
Recent applications of the Birthday Repetition technique have demonstrated the quasi-polynomial time hardness in various computational problems, including AM with k provers, Dense CSPs, Free games, and Nash equilibria. These applications also explore the potential implications in signaling theory an
0 views • 18 slides
Finding Reductions in NP-Hardness Proofs
To find a polynomial-time many-one reduction from a known NP-hard decision problem A to a target problem B, ensure that the reduction maps inputs correctly such that the output for A is 'yes' if and only if the output for B is 'yes.' An example is demonstrated using Subgraph Isomorphism and Hamilton
0 views • 32 slides
Types in Programming Languages: Lecture Insights
The lecture delves into the intricacies of types in programming languages, focusing on simply-typed Lambda-Calculus, safety, preservation, progress, and extensions like pairs, datatypes, and recursion. It discusses static vs. dynamic typing, Curry-Howard Isomorphism, subtyping, type variables, gener
1 views • 73 slides
TopK Interesting Subgraph Discovery in Information Networks
Discovering top-K interesting subgraphs in information networks is crucial for various applications like network bottlenecks, team selection, resource allocation, and more. This research focuses on developing low-cost indexes and novel algorithms to efficiently detect these subgraphs. The contributi
0 views • 26 slides
Greedy Algorithms: Minimum Spanning Tree Analysis
Explore the concept of Minimum Spanning Tree (MST) in the context of greedy algorithms, focusing on Kruskal's Algorithm. Understand the methodology behind selecting the minimum weighted subgraph that connects all vertices in a weighted graph efficiently. Delve into problem-solving strategies and app
2 views • 39 slides
Algebraic Homomorphisms and Singular Transformations in Mathematics
An exploration of Cayley's theorem analog for groups in algebra, showcasing the isomorphism of algebras with unit elements over fields to subalgebras of some vector space. Additionally, a discussion on characterizing singular transformations in finite-dimensional vector spaces over fields. The expla
0 views • 14 slides
Minimum Spanning Trees in Graph Theory
Exploring the concept of minimum spanning trees in undirected, weighted graphs. A spanning tree is a connected acyclic subgraph that includes all vertices of the original graph. The Minimum Spanning Tree (MST) problem involves finding the tree with the smallest total edge weight. The cycle property
0 views • 42 slides
Subgraph Matching for Cloud Service Placement in Datacenters
This research explores the efficient placement of cloud services in datacenters through subgraph matching, focusing on compatibility and resource optimization between customers and providers in cloud computing environments. The study highlights challenges in dynamic subgraph matching and the limitat
1 views • 29 slides
Interactive Protocols in Arthur-Merlin Games for Graph Nonisomorphism
Explore the concept of interactive protocols in Arthur-Merlin games for determining graph nonisomorphism. Arthur, a powerless knight, seeks to trust Merlin's advice but Merlin, all-powerful yet untrustworthy, must find ways to convince Arthur. Utilizing randomness, the games delve into graph isomorp
0 views • 13 slides
Interactive Proofs in Complexity Theory
Delve into the realm of interactive proofs in complexity theory, exploring concepts such as completeness, soundness, and efficiency. Discover how interactive proof systems can be utilized in scenarios like graph isomorphism and their implications on the complexity classes NP and coNP. Uncover the in
1 views • 40 slides
Efficient Bitruss Decomposition for Large-scale Bipartite Graphs
Bitruss decomposition is a powerful concept in graph theory to identify cohesive subgraphs in bipartite graphs. This paper by Kai Wang, Xuemin Lin, Lu Qin, Wenjie Zhang, and Ying Zhang presents an efficient approach for computing bitruss numbers of edges in large-scale bipartite graphs. The study ex
0 views • 25 slides
Efficient Cut Algorithms in Graph Structures
This content covers efficient cut algorithms in graph structures, focusing on partitioning graph vertices, computing minimum-cut values, and a short history of min-cut algorithms. It explains the contraction algorithm, cut sparsifier subgraph computation, and the general contraction algorithm. The m
0 views • 25 slides
Frequent subgraph mining
In this overview, we delve into various aspects of frequent subgraph mining, discussing types of graphs, analyzing graphs for data mining tasks, input-output processes, and the goal of discovering repeated subgraphs in graph databases.
1 views • 13 slides
CS 1501 RECITATION 6
The Minimum Spanning Tree Problem involves finding the connected subgraph with the smallest weight in a weighted graph, important for real-world applications like network design. Prim's Algorithm is a well-known method for constructing a minimum spanning tree efficiently. This algorithm selects edge
0 views • 45 slides
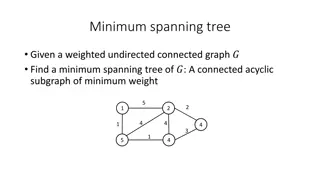
Minimum spanning tree
In the realm of graph theory, the quest for the minimum spanning tree in weighted undirected connected graphs is a crucial pursuit. This involves finding a connected acyclic subgraph with the least total weight, paving the way for efficient network optimization and resource allocation.
0 views • 26 slides
Introduction to Graphs
Graph theory is a fundamental concept in computer science, allowing us to model and solve various problems. This lecture delves into the Seven Bridges of Konigsberg problem, exploring degrees, isomorphism, paths, cycles, connectedness, trees, and Eulerian cycles. By examining Euler's solution, we se
0 views • 67 slides
Operator Scaling by Yuanzhi Li and Collaborators: Group Actions & Orbit Intersection Problems
This paper delves into the fascinating realm of operator scaling discussed by Yuanzhi Li from Princeton University in collaboration with other researchers. The focus is on group actions and problems related to orbit intersection, offering insight into graph isomorphism, complexity levels, and an eff
0 views • 60 slides
Colorful Connected Graph Problem Overview
The Colorful Connected Graph Problem involves finding a connected subgraph with a minimum number of vertices containing at least one vertex of each color. Considered an NP-complete decision problem, it has various real-world applications in fields such as Protein-Protein Interaction Networks, Sensor
0 views • 46 slides
Graph Theory: Euler Paths and Circuits in Management Science
Euler Paths and Circuits in Graph Theory and Management Science, illustrated through the famous Konigsberg bridges problem and graph theory concepts. Understand vertices, edges, isomorphism, and graph modeling of relationships with examples like housing developments and student friendships.
0 views • 17 slides
Modeling Mass Protest Adoption in Social Networks Using Geometric Brownian Motion
This study explores the adoption of mass protests in social network communities through the application of Geometric Brownian Motion. The research delves into the dynamics of protest participant growth, the underlying social network structures, and the trust functions modeled as a GBM process. Addit
0 views • 11 slides
Chern-Simons Terms in Heterotic Theory
The implications of Chern-Simons terms and heterotic superpotentials in string theory, focusing on the mathematical definitions, Bianchi identity conditions, and real isomorphism of vector bundles. Discover the significance of these concepts in moduli stabilization and understanding E8 bundles.
0 views • 11 slides
Network Design with Degree Constraints: Problems and Results
Delve into the complexities of network design with degree constraints as outlined in the joint work by Guy Kortsarz, Rohit Khandekar, and Zeev Nutov. Explore various minimum-cost spanning subgraph scenarios, arborescence/tree spanning challenges, and prize-collecting Steiner network designs with deg
1 views • 17 slides
Embedding-Based Subgraph Isomorphism for Bug Detection
Explore how SICode utilizes embedding-based subgraph isomorphism identification to detect bugs in code efficiently. Learn about the challenges in subgraph matching algorithms and the solution offered by graph neural networks. Dive into the approach of SICode in training embedding models and detectin
0 views • 20 slides
Dynamic Graph Neural Networks for Anomaly Detection in Time Series
Explore how DGNN utilizes dynamic graph neural networks to detect anomalies in multivariate time series data efficiently. The approach includes Dynamic Subgraph Generation and Adaptive Graph Attention Network for precise learning of temporal relationships, outperforming traditional methods like PCA
1 views • 16 slides
Diversified Top-k Subgraph Querying in Large Graphs - Problem Definition and Solutions
Explore the problem of top-k subgraph querying in large graphs, aiming to provide diversified results with reduced overlap. Learn about the challenges, naive solutions, and proposed algorithms, including Ullmann framework and diversified top-k maximal clique approach.
0 views • 19 slides
Financial Failure and Corporate Intervention at Northamptonshire County Council: A Case Study
Explore the financial failure and corporate intervention at Northamptonshire County Council, shedding light on the background, unique aspects, and government response. Delve into the intervention triggered by a Section 114 notice under the LG Finance Act, with a focus on local government re-organiza
0 views • 16 slides
Handling Exceptions in JUnit Testing with JSON and Isomorphism Techniques
Learn how to handle exceptions effectively in JUnit testing by exploring examples involving JSON manipulation and Isomorphism techniques. Enhance your understanding of error handling strategies in software development with detailed code snippets and explanations.
0 views • 4 slides
Understanding Output-Sensitive Enumeration of Structures like Trees and Graphs
Explore the concept of output-sensitive enumeration focusing on isomorphism, rooted trees, necklaces, and more. Learn about the challenges of avoiding duplicates in structured data and how isomorphism plays a critical role in identifying unique structures.
0 views • 77 slides
Graph Isomorphism: Examples and Concepts
Explore examples of isomorphic and non-isomorphic graphs, understand the concept of graph isomorphism, discover different properties to determine isomorphism, and learn through graphical representations and node mappings.
0 views • 18 slides
Understanding Isomorphism and Invertibility in Linear Algebra
Learn about the concepts of isomorphism, invertibility, one-to-one transformations, bijective transformations, singular transformations, isomorphic vector spaces, and a key theorem in linear algebra. Explore the fundamental definitions and properties of these topics with illustrative images and expl
0 views • 12 slides
Understanding the Power of WL[k] Graph Isomorphism
Discover the evolution of WL[k] graph isomorphism through the early insights and conjectures of Martin Fér, alongside the counterexample that challenged established beliefs. Explore the algorithm behind 3-dim WL Refinement and the intriguing case of non-isomorphic graphs sharing a meta-graph struct
0 views • 21 slides
Understanding Graphs and Trees: Definitions, Properties, and Representations
Explore the fundamental concepts of graphs, including vertices, edges, directed and simple graphs, complete graphs, subgraphs, Euler circuits, and more. Dive into matrix representations, planar graphs, and graph isomorphism for a comprehensive overview.
0 views • 16 slides































![Understanding the Power of WL[k] Graph Isomorphism](/thumb/413724/understanding-the-power-of-wl-k-graph-isomorphism.jpg)
